Research diaries #11: rearranging sequences, weirdness at infinity

At infinity our ordinary intuitive understanding breaks down as the mathematical definition of infinity is very different from what we have in our mind. A good example of this concerns rearrangements of infinite sums. Let's just take an example, we consider the following:

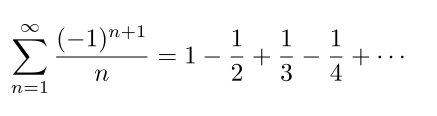
Denote the sum of the first n-elements by s_n. Then, we can see that s_n homes in on a specific value. More specifically, s_n is oscillating around that value. Let us not concern ourselves with the exact value but let us just call the limiting value S. We make the additional observation that S>0. This will be important later.

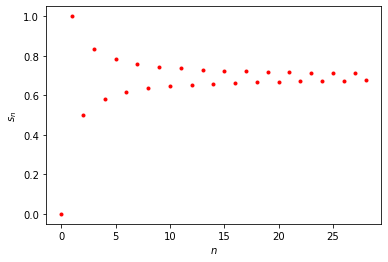
Do the plusses and minuses that make up the infinite sum still work as when we are considering finite numbers? Well, let's try and see what happens. We will add S to S/2 in the following way:

So we add the terms in the blocks to arrive at the bottom equation. This is a rearrangement of the terms in S. But if that rearrangement is equal to S we would get a weird contradiction because that would imply that S is equal to zero which clearly cannot be the case.

The reason is that we cannot just rearrange terms in an infinite sum. A simpler example is

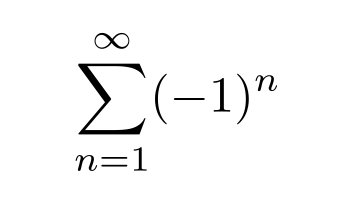
which could be rearranged to 0, 1 or -1.

So is rearranging absolutely illegal when infinite sums are concerned. Well, if the sum converges absolutely then any rearrangement will converge to the same value (for the exact result with proof see Theorem 2.7.10 in Abbot's Understanding Analysis, the proof makes use of the property that if you go far enough in the rearrangement of the sequence the differences between the sums can be chosen arbitrarily small).

Infinity does not satisfy the rules of our intuition. It requires us to make statements rigorous if we still want to stay scientific.

Reference: This nice example is taken Understanding Analysis by Abbot which is an absolute must read for undergrad math students ^^