Controllability and Observability of a System in State Space
1. Introduction
We explain the controllability and observability of a system. Controllability describes the ability of the control (input) signal u(t) to control the response of the state variables of the system that allows the system to change from the initial state to any time interval. On the other hand, observability describes the ability to deduce the system response from the output. Also, observability gauges the system for observer design.

Figure 1: Electrical circuit of the given system
In this post, we evaluate the controllability and observability of the given system, shown in Figure 1. The given system was described in the previous post including the state space model and its system's transfer function. In the next section, the mathematical models for controllability and observability is discussed in details with MATLAB.
2. Controllability
In this section, we investigate the controllability of a system. The system is controllable when the input takes every state variables from a desired initial state; otherwise, the system is uncontrollable. The control signal, u, able to control the behavior of all state variables. If the control signal, u, cannot control the state variable, we are unable to design the state feedback of the system.
We have two option to determine the controllability of the system. We can perform controllability by inspection that uses the decoupled representation of the system or controllability via the controllability matrix. In this paper, the latter is adapted hence controllability by inspection only feasible when the system is represented in parallel form.
2.1 The Controllability Matrix
Controllability via the controllability matrix allow testing for controllability or designing the state feedback of a plant regardless of the system representation. The controllability matrix gives a system model that expressages all state variables are to be controlled by the plant input, u. The controllability matrix, CM, is defined as
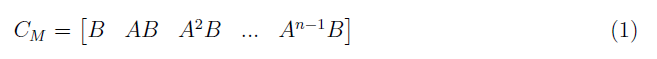
for the nth-order plant whose state equation

is controllable. In this part, we defined the controllability matrix for the system (shown in Figure 1) whose state space model is given as
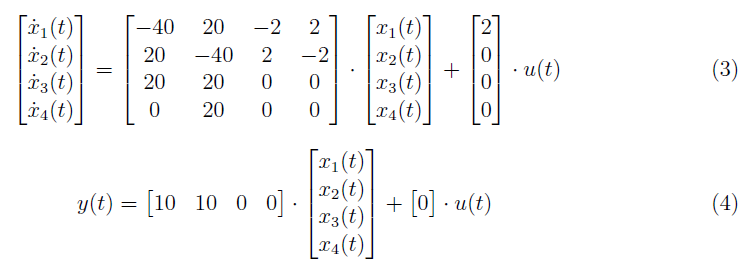
From equation (3), the controllability matrix is formed as
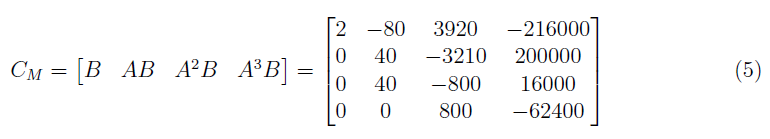
wherein it has a rank of 4 and a determinants of 1.9456 × 108. The controllability matrix, rank and determinants are generated by running the MATLAB script in listing 1.
%state space model of the system
A = [-40 20 -2 2 ; 20 =40 2 =2 ; 20 20 0 0 ; 0 20 0 0 ] ;
B = [ 2 ; 0 ; 0 ; 0 ] ;
C = [ 1 0 10 0 0 ] ;
D = [ 0 ] ;
%c o n t r o l l a b i l i t y ma t rix
CM = [B A*B (Aˆ2 ) *B (Aˆ3 ) *B] ;
rCM = rank (CM) ; %rank
dCM = de t (CM) ; %determinant
We can conclude that the system is controllable hence the rank and the system order is equal. The controllability of a system is better to visualized in parallel form (decoupled) where the system matrix is diagonal and the roots are distinct.
3. Observability
The system is said to be observable when an initial state vector, x(t0), is found from u(t) and y(t) is measured across a finite time interval from t0; otherwise, the system is unobservable. Observability is the ability to work out the state variables from the known input, u(t) and output, y(t). Similar to controllability, the observability of a system is better visualized with diagonalized system. Observability via inspection limits only to system representation in parallel form. These technique discriminates the other alternative representation or models for the system. In this paper, we adapt observability via the observability matrix wherein it gives a flexible option in testing observability of a system regardless of the system representation.
3.1 The Observability Matrix
Observability via the observability matrix allow testing for observability with regards to any system representation of choice. The observability matrix gives a system model that expressages all state variables are observed at the output. We defined the observability matrix as

for the nth-order plant whose state output equation y(t) = Cx(t) + Du(t) is observable. In this part, we defined the observability matrix for the system with the state output equation is given as
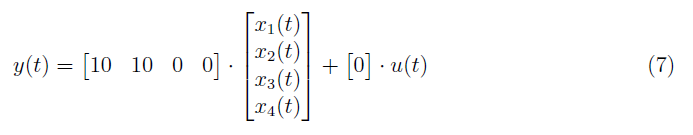
From equation (7), the observability matrix is defined as
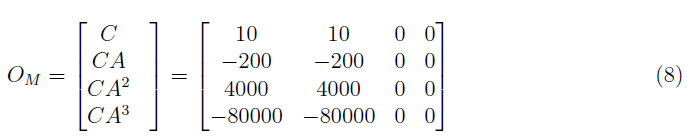
wherein it has a rank of 1 and a determinant of 0. The observability matrix, rank and determinants are generated by running the MATLAB script in listing 2.
%observability matrix
2 OM = [C; C*A; C*(Aˆ2 ) ; C*(Aˆ3 ) ] ;
3 rOM = rank (OM) ; %rank
4 dOM = det (OM) ; %determinants
The system is unobservable hence the determinant is zero and rank is unmatched to system order.
4. Conclusion
Controllability and observability evaluates a system to deduce a controller and observer design from the input and the output signal respectively. In the previous section, we specifically used the controllability and observability matrix to determine whether the system can be deduce from its input and output. For controllability, the system is controllable based on the rank and the determinants of the controllability matrix. In contrast, the system is unobservable hence it has a determinants and a rank is unmatched to the system order.
5. References
[1] Norman S. Nise. Control Systems Engineering (7th. ed.). 2015. John Wiley & Sons, Inc., USA.
[3] Bishop, Robert H., and Richard C. Dorf. "Modern control systems." (2017).
[4]Analysis of observability and controllability of nonlinear dynamic systems by linear methods
(Note: All images in the text is created by the author (@juecoree) except those with separate citation.)
Interested in my previous articles, here is a list:
Control System:
1. State Space Model and System Transfer Functions
2. System Identification using MATLAB and Simulink
3. Time Domain, Zero Input and Zero State Response
4. Decoupling a System in State Space
Robotics:
1. Forward and Reverse Kinematics for 3R Planar Manipulator
2. Forward Kinematics of PUMA 560 Robot using DH Method
3. Inverse Kinematics of PUMA 560 robot
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Your post has been voted as a part of Encouragement program. Keep up the good work!
Try https://ecency.com and Earn Points in every action (being online, posting, commenting, reblog, vote and more).
Boost your earnings, double reward, double fun! 😉
Support Ecency, in our mission:
Ecency: https://ecency.com/proposals/141
Hivesigner: Vote for Proposal