Alternative Representation of State Space
Modelling dynamical system in state space can take multiple representations. These representations observes the system in a different perspective. Naturally, state space is in phase variable form but state space models can be viewed in the perspective of an observer or a controller. These representations have similar system response even with different model.
In this blog, we explores the responses of each representation and find out whether multiple models of a given system have similar responses. We used MATLAB and Simulink to convert each signal flow graphs into a block diagram so that we can observe the time response of each models. We also explain the difference between each representation as to what it is intended to view the system.
2. Phase Variable Form

Figure 1: Decomposed transfer function (block diagram)
In this section, we examine the phase variable of the system’s state space model. Given the transfer function for the system as
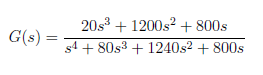
We decomposed the transfer function o find the state space model, as shown Figure 1. By separating the system into two cascaded blocks, we can easily obtain the state space model. We derived the state space in phase variable form using the decomposed transfer function. We consider that the transfer function follows
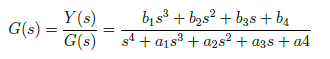
and state variables as
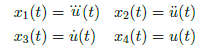
to get
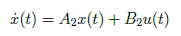
where
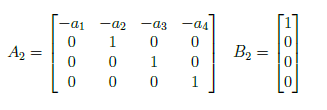
Then, consider that
where
The state space representation in time domain is
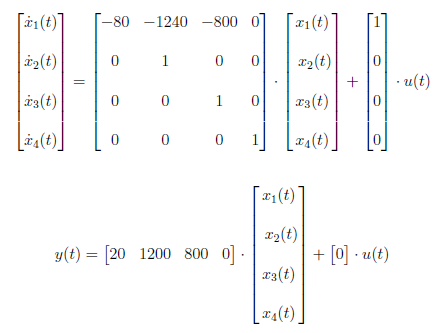
We take the Laplace transform of the earlier state space equation and get the state space equation in phase variable form as

We can also represent the state space in phase variable form by means of a signal flow graph in Figure 2.
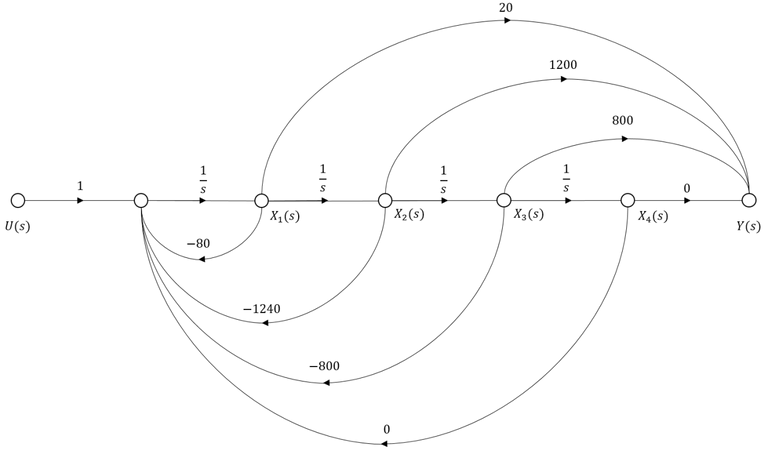
Figure 3: Phase Variable Form
In Simulink, we represent the signal flow graph in block diagram to observe the system response as to the phase variable form. The block diagram is shown in Figure 3. We set a chirp signal for input U(s) and display the output Y(s) response curve. The chirp signal is generated by running the MATLAB script below. The simulation result is displayed in Figure 4.
%Setting up chirp signal
t = 0:0.0001:30;
t1 = [0:0.0001:60]';
y = chirp(t,0,60,10);
x = wrev(y(1,1:end-1));
xa = [y x]';
x1 = [t1 xa];
plot(t1,xa);
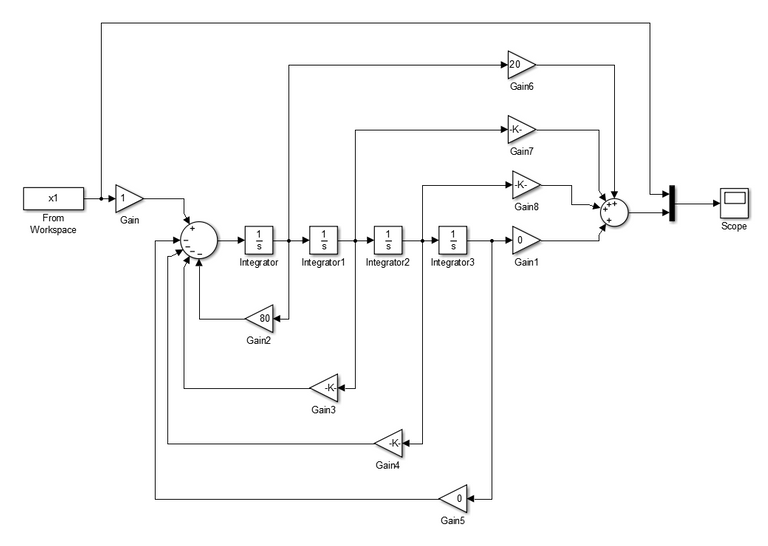
Figure 3: Blok Diagram for Phase Variable Form (Simulink)
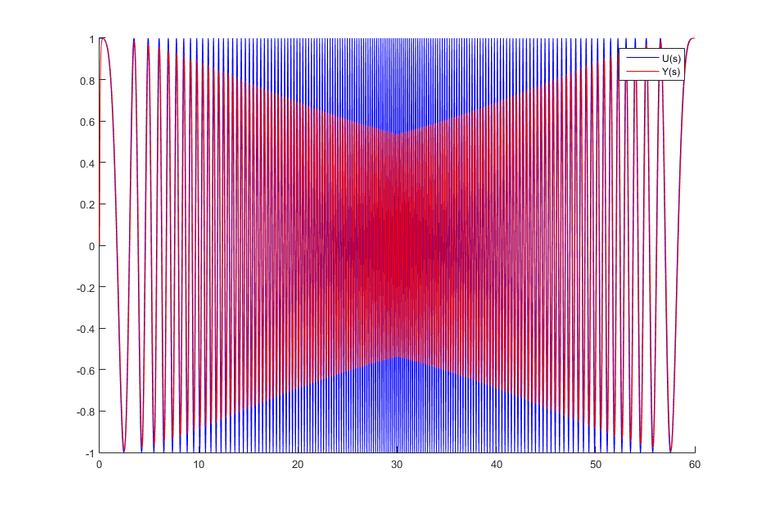
Figure 4: Input and Output of the Phase Variable Form
3. Controller Canonical Form
The controller canonical form is used for design of controllers. Also, the controller canonical form is used to investigate the controllability of a system. The control signal, U(s), able to control the behavior of all state variables in the system. We derive the controller canonical form by reversing the order of state variables of the state space model in section 2. Reversing the order of state variables yield to
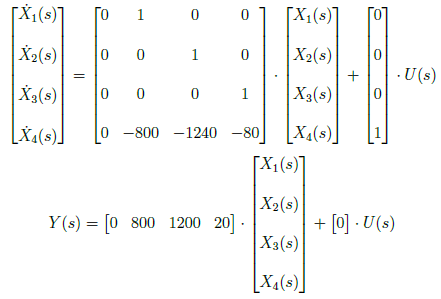
The controller canonical form is represented by the signal flow graph in Figure 4. The difference between phase variable and the controller canonical form is the variables in the signal flow graph are interchanged.
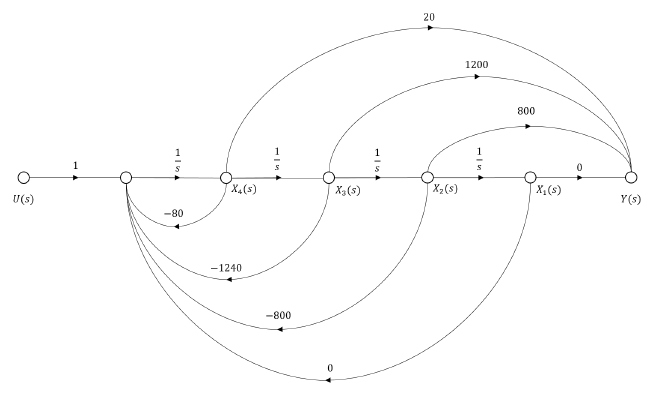
figure 4. Controller Canonical Form
In Simulink, we have similar block diagram representation as to the phase variable form, as shown in Figure 5. Similar to section 2, we feed a chirp signal at the input of the controller canonical form and generate the response curve. Hence only the placement of state variables are interchanged, the system generates the same response (as expected).

Figure 5: Blok Diagram for Controller Canonical Form (Simulink)

Figure 6: Input and Output of the Controller Canonical Form
4. Observer Canonical Form
The observer canonical form yields the left companion matrix and is used for designing of observers. We used the transfer function in section 2 to derive the observer canonical form. Cross-multiplying yields
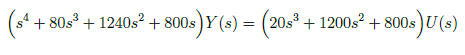
Then, we divide all the terms by the highest power of s, s4, and we get
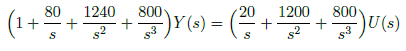
Combining terms of like powers of integration gives
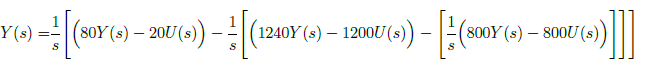
The terms in earlier equation must be integrated as to the power of s. The first term integrated once, second term by twice and so on until nth term. The relationship between state space matrices in controller and observer canonical form are
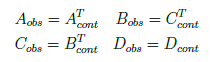
We have state space equation in observer canonical form as
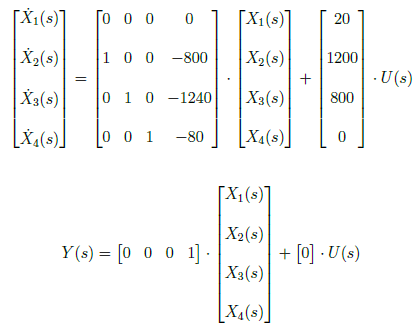
The observer canonical form is represented by the signal flow graph shown in Figure 5. In Simulink, we build a block diagram that represents the observer canonical form of the system, shown in Figure 8. We apply chirp signal at the input of the observer canonical form and generate the response curve in Figure 9. There is an observe slight spike in the response curve of the observer canonical form at 60 second interval. Overall the response curve of the observer canonical form is the same as to the phase variable and controller canonical form.
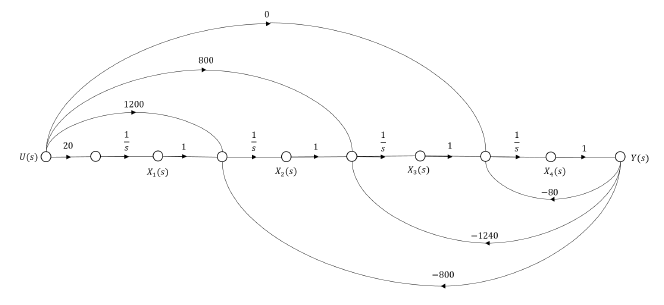
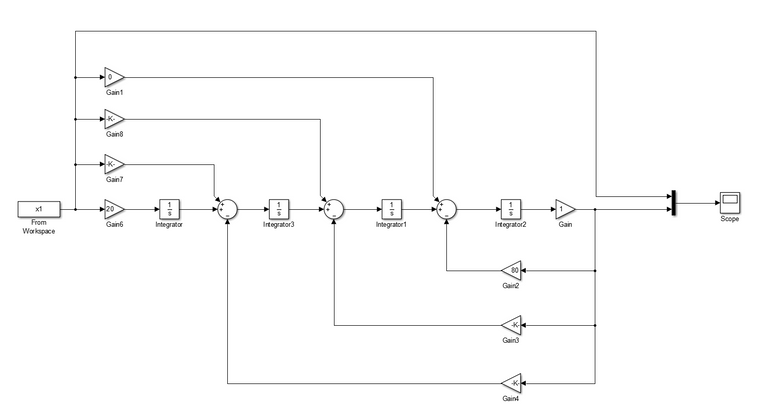
Figure 8: Block Diagram for Observer Canonical Form (Simulink)
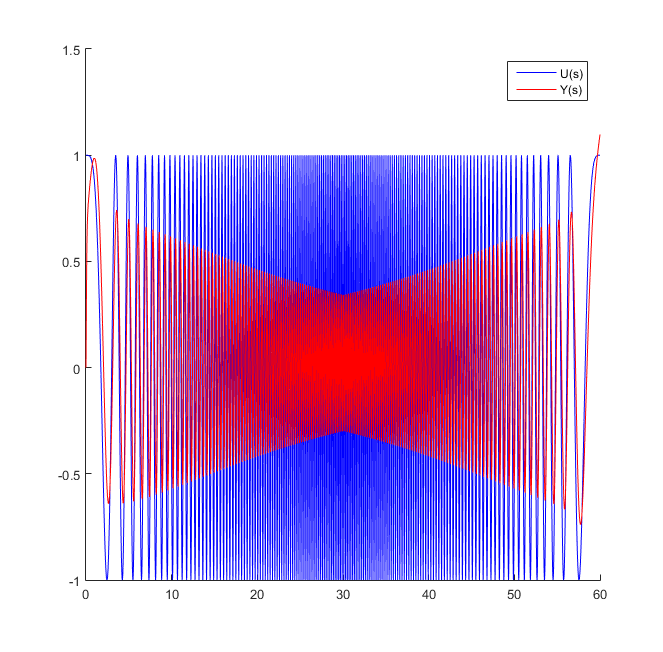
Figure 9: Input and Output of the Observer Canonical Form
5. Conclusion
In this blog, we derived the alternative representation of a state space model. We represent the state space equation into phase variable, controller canonical and observer canonical forms. The phase variable form is obtained by applying Laplace transform to the time-domain state space equation. Meanwhile, we interchange the state variables in reverse order to obtain the controller canonical form. We observed from Figures 3 and 4 that X1(s) and X3(s) are interchanged. The observer canonical form consist of transpose matrices from the canonical form except for D matrix. The input matrix, B, is a transpose matrix of C vector in controller canonical form while output matrix, C is a transpose of the B vector in controller canonical form. Thus, observer and controller canonical form are dual.
6. References
[1] Norman S. Nise. Control Systems Engineering (7th. ed.). 2015. John Wiley & Sons, Inc., USA.
[3] Bishop, Robert H., and Richard C. Dorf. "Modern control systems." (2017).
[4] Rowell, Derek. "State-space representation of LTI systems."
(Note: All image in the text is drawn by the author except those with attached citations.)
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.