El semiconductor CuGa3Te5 y su caracterización óptica

Bienvenidos nuevamente a mi HIVE BLOG

[@iamphysical](https://stem.openhive.network/#!/@iamphysical)

Hoy 18 de septiembre de 2020 comenzaré felicitando a todos los chilenos que festejan sus Fechas Patrias en un compartir familiar y con las medidas higiénicas necesarias para evitar la propagación del COVID-19. Por otra parte, en este artículo les presentaré algunos resultados experimentales sobre la composición química y transiciones térmicas, así como la caracterización óptica del semiconductor ternario CuGa₃Te₅

Introducción

En publicaciones anteriores les había platicado sobre los materiales semiconductores básicos Silicio y Germanio, los compuestos binarios CdS y ZnO, así como los semiconductores ternarios CuInSe₂ y CuInTe₂. Mi publicación será acerca del semiconductor ternario CuGa₃Te₅, el cual tiene 1 vacancia de cationes en su fórmula molecular.

Los compuestos de Cu de la familia I-III₃-VI₅ tienen deficiencia de 1 catión en comparación con el número de sus aniones. Por esta razón a estos materiales se les llaman “Compuestos con Vacancias Ordenadas” (CVO) y su fórmula química se escribe como:

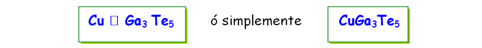
donde  representa la vacancia del catión, y se considera como un átomo que aporta cero electrones para cumplir la regla de 4 electrones por sitio en la red (Grim-Sommerfeld):

Esta manera de escribir la fórmula química anexando un símbolo vacío para representar a 1 de las vacancias presentes de manera ordenada en la estructura cristalina constituye un artificio para "hacer cumplir" la regla de Pamplin o con las excepciones a la Regla del Octeto.

Por otra parte, Zhang et al. [1] han mostrado que los pares de defectos donor-aceptor “PDDA” en CuInSe₂ se forman fácilmente en este compuesto en comparación con lo observado en los compuestos binarios, con energá de formación de 0,20 eV/par en Cu-Ga-Te. Los materiales ricos en Ga se forman como una repetición de una unidad de los PDDA en cada n = 4, 5, 6, 7, 8 y 9 unidades de CuInSe₂, representados por la fórmula: Cu_n-3In_n+1Se_2n

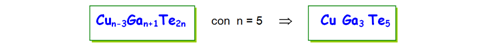
Wei [Appl. Phys. Lett. 72, 3199 (1998)] reporta una energía de formación de los pares de defectos (Ga_Cu⁺² + 2V_Cu^-1) = 0,20 eV/par, por lo que es común ver que a estos semiconductores ternarios también se les llame “Compuestos con Defectos Ordenados” (CDO).

En el desarrollo de este artículo tendremos en cuenta el cumplimiento de los siguientes objetivos:

• Determinar la estequiometría y transiciones térmicas del compuesto CuGa₃Te₅
• Estudiar la Cola de Urbach observada a diferentes temperaturas entre 50 y 300 K en este semiconductor

La fórmula química de los CVO o CDO es Cu₁III₃VI₅ y su relación estequiométrica ideal es 1:3:5 en porcentaje Al determinar la composición química mediante la técnica de dispersión de energía de rayos X, se obtuvieron los siguientes valores en porcentaje atómico:

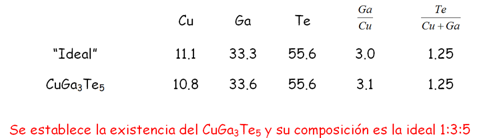
Transiciones Térmicas

Para determinar el punto de fusión de este semiconductor, así como los cambios de fases en el estado sólido y la posible presencia de fases secundarias, realizamos el Análisis Térmico Diferencial (ATD) empleando el siguiente equipamiento: 1) horno vertical de 1 zona de temperatura (hasta 1200 ºC), 2) registrados de 2 plumillas (rojo y verde) con las variables V-t y 3) papel milimetrado con escala adecuada para convertirlas a Temperatura.

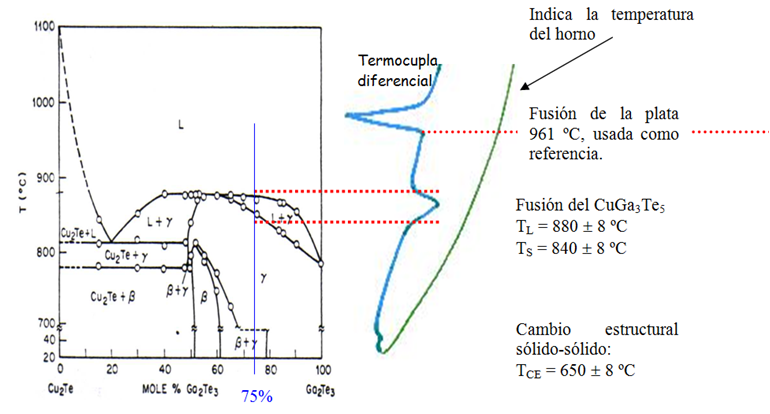
En el termograma vemos ahora en línea contínua de color verde la que nos indica la temperaura dentro del horno vertical y en línea de color azul se destacan las discontinuidades relacionadas con las transiciones térmicas debidas al punto de fusión (880 ºC) y cambio estructural en el estado sólidos (650 ºC), los cuales corresponden muy bien con el diagrama de fases de los pseudobinarios Cu₂Te - Ga₂Te₃.

Por cierto, la fusión incongruente puede dar lugar a defectos físicos en el lingote y también desviación de la estequiometría ideal, ya que existe una diferencia de 40 ºC entre el momento que comienza la solidificación (aparecen los primeros cristales de CuGa₃Te₅) y cuando se forma el lingote sólido.

Colas en las Bandas de Energía

Estudios teóricos sobre la estructura de bandas conducen a la hipótesis que el desorden estructural debido a la desviación de la estequiometría, vacancias y a los PDDA, pueden introducir niveles de energía en la brecha de energía prohibida de un semiconductor.

Se ha sugerido que la parte exponencial del borde de absorción (B) es una evidencia de tales estados localizados.

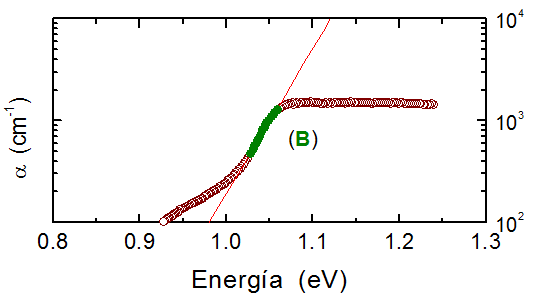
Variación logarítmica del coeficiente de absorción (α) con la energía del fotón incidente (hα) a varias temperaturas entre 100 y 300 K, justo por debajo de la absorción fundamental.

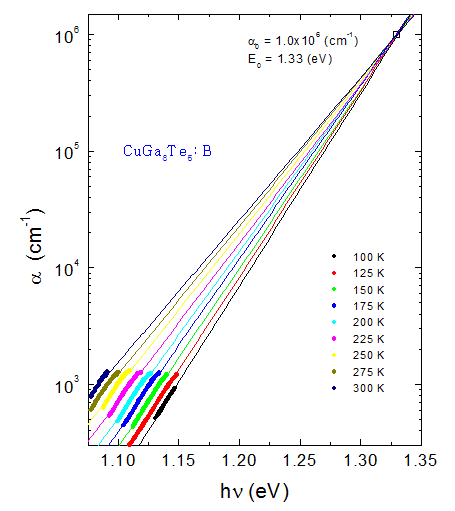
Se observa una dependencia lineal de α para cada temperatura. La extrapolación de estas líneas convergen a un mismo punto definido por E₀ = 1.33 eV y α₀ = 1.0x10⁶ cm^-1. Este comportamiento satisface la regla de Urbach [2] que es expresada como:

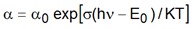
donde σ es el parámetro relacionado con la inclinación de la extrapolación lineal y es inversamente proporcional a la interacción electrón/excitón-fonón y K es la constante de Boltzmann.

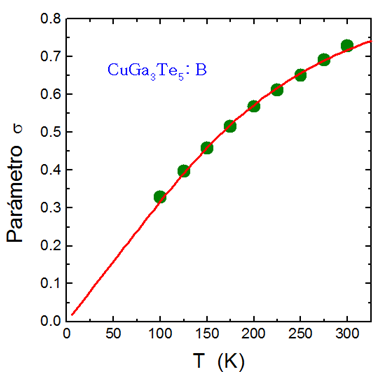
Este tipo de dependencia del parámetro σ con la Temperatura se ajusta mediante la relación:

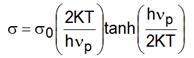
donde σ₀ es un término independiente de la temperatura y hν_p corresponde a la energía de los fonones que está asociada con la cola de Urbach. Los valores obtenidos de este ajuste son σ₀ = 0.93(2) y hν_p = 50(2) meV, los números entre paréntesis corresponden al dígito que incurre en error.

En varios semiconductores se ha encontrado que hν_p es mayor que el promedio de los diferentes modos ópticos reportados en la literatura [3,4]. En algunos casos es mucho mayor que los modos más altos. Se ha sugerido que esto tiene su origen en los defectos estructurales del material relacionados a las vacancias e intersticiales de los cationes.

Es importante resaltar que la variación de la Energía de Urbach (E_U = KT/σ) con la Temperatura debería aumentar en algunos meV debido a la generación de más estados localizados y la concentración de los portadores de carga también se incrementa.

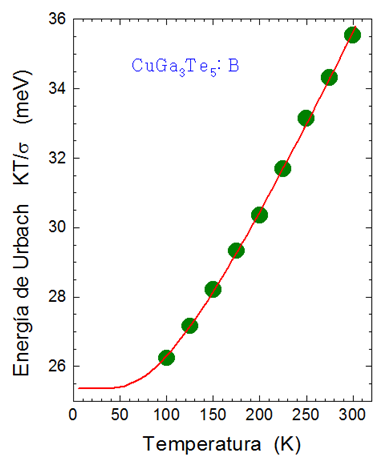
Esta dependencia se ajustó con una relación empírica [5] que toma en cuenta el efecto del desorden estructural P y la contribución térmica de los fonones N que se ve afectada por las PDDA y la vacancia de catión. Esto se expresa como:

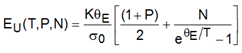
De nuevo resalto la importancia del estudio teórico y experimental de estos materiales semiconductores, pues abren las puertas al inicio de líneas de investigación y aplicación de "nueva" física por la aparición de estados energéticos adicionales debido a los pares de defectos y desviación de la estequiometría. Lo digo porque en la ecuación anterior, junto a nuestro grupo de trabajo agregamos el parámetro N para representar a la fracción de esos estados localizados que contribuyen en la formación de las colas de Urbach.

Los resultados de este ajuste son P = 1.0(1), N = 0.61(2) y θ_E = (200 ± 27) K. El valor de θ_D = (267 ± 27) K, calculado de la relación θ_E ∝ ¾θ_D, corresponde muy bien con el valor promedio θ_D = 246 K calculado a través del ajuste de la curva de E_G vs T.

Conclusiones

1. Se ha establecido la existencia del compuesto semiconductor CuGa₃Te₅ y su composición estequiométrica corresponde a la ideal 1:3:5.
2. Las transiciones térmicas determinadas por ATD, corresponden a la temperatura de fusión y cambio estructural en el estado sólido y que están de acuerdo con las temperaturas del diagrama de fases reportado por Palatnik y Belova.
3. La temperatura de Debye calculada a partir del ajuste de E_U vs T concuerda con el valor obtenido del análisis de la variación de la brecha de energía con la temperatura. Una relación empírica propuesta recientemente, explica la variación de la Energía de Urbach con la temperatura y se concluye que la energía del fonón involucrada en la formación de la cola de Urbach se debe a la contribución de los modos localizados originados por los pares de defectos ordenados.

Referencias

[1] S. B. Zhang, Su-Huai Wei, and Alex Zunger. Phys. Rev. B, 57, 9642 (1998).
[2] F. Urbach. Phys. Rev., 92, 1324 (1953).
[3] C. Rincón, S. M. Wasim, R. Márquez, L. Nieves, G. Marín, E. Hernández, J. Galibert. J. Phys. Chem. Solids, 63, 581 (2002).
[4] E. Hernández, C. Rincón, S. M. Wasim, G. Marín, P. Bocaranda, G. Sánchez Pérez, A.E. Mora e I. Molina. Rev. Téc. Ing. Univ. Zulia, 22, 189 (1999).
[5] S. M. Wasim, C. Rincón, G. Marín, P. Bocaranda, E. Hernández, I. Bonalde and E. Medina. Phys. Rev. B, 64, 195101-1 (2001).

En nuestra comunidad se promocionan y valoran las publicaciones de alto impacto relacionados con Ciencia, Tecnología, Ingeniería y Matemáticas, dale clic a la etiqueta #STEMSocial, para que te enteres de nuestro trabajo de calidad científica y grado semiconductor!