Hablemos sobre Gauss y su ley que relaciona la Carga Eléctrica y el Campo Eléctrico
Hace varios días, comenzamos a desarrollar el tema concerniente a flujo eléctrico, conceptos de simetría y ejemplos cualitativos de flujo, el día de hoy daremos continuidad a este importante tema, hablaremos sobre Gauss y su ley.

Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.
Antes de comenzar a desarrollar el tema, es importante hablar sobre Johann Carl Friedrich Gauss quien era un matemático, astrónomo y físico alemán, quien realizo diversas contribuciones como la teoría de los números, la geometría diferencial, el análisis matemático, la estadística, el álgebra, la óptica y muchos más. A este extraordinario personaje se le conocía como Príncipe de los matemáticos por su notable influencia en diversos campos de la matemática y las ciencias en general. Gauss provenía de una familia campesina, con padres de poca cultura, su mama sabía leer, mas no escribir, y su padre sí, pero en cuanto a las matemáticas no pasaba de las aritméticas elementales.
Uno de sus más interesantes aportes es la Ley de Gauss, la cual resulta como una alternativa de la ley de Coulomb, pero la ley de Gauss ofrece una alternativa diferente de expresar la relación que existe entre la carga eléctrica y el campo eléctrico. Dicha ley establece que “el flujo eléctrico total a través de cualquier superficie cerrada es proporcional a la carga eléctrica total (neta) dentro de la superficie” Zemansky (2009). En publicaciones anteriores pudimos observar cualitativamente esta relación para algunos casos, ahora lo veremos con más rigor.
Si se coloca la carga en el centro de una superficie esférica imaginaria de radio R, la magnitud E del campo en todos los puntos de la superficie, vendrá dada por la expresión:
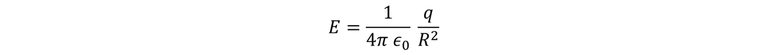
En cada uno de los puntos de la superficie, E es perpendicular a ésta y su magnitud es la misma en todos los puntos. El flujo eléctrico es sencillamente el producto de la magnitud del campo E por el área total.
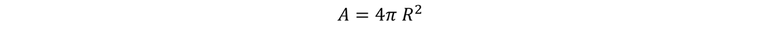
Por lo que:
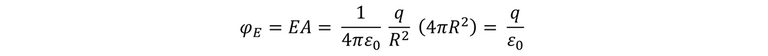
De lo cual podemos concluir que el flujo es independiente del radio de la esfera, sino que su dependencia es únicamente de la carga encerrada.
Si esta vez analizamos un objeto cuya forma no sea esférico, sino más bien con una forma irregular como la imagen que se muestra a continuación. Si consideramos un elemento pequeño de área dA sobre una superficie irregular, podemos observar que dicha área es más grande que el elemento correspondiente sobre una superficie esférica la cual está a la misma distancia de q. Si una normal a dA forma un ángulo φ con una línea radial que proviene de q, dos lados del área proyectada sobre la superficie esférica son reducidos por un factor de cos φ. Por otra parte, los otros dos lados no cambian, por lo que el flujo eléctrico a través del elemento correspondiente de la superficie irregular.
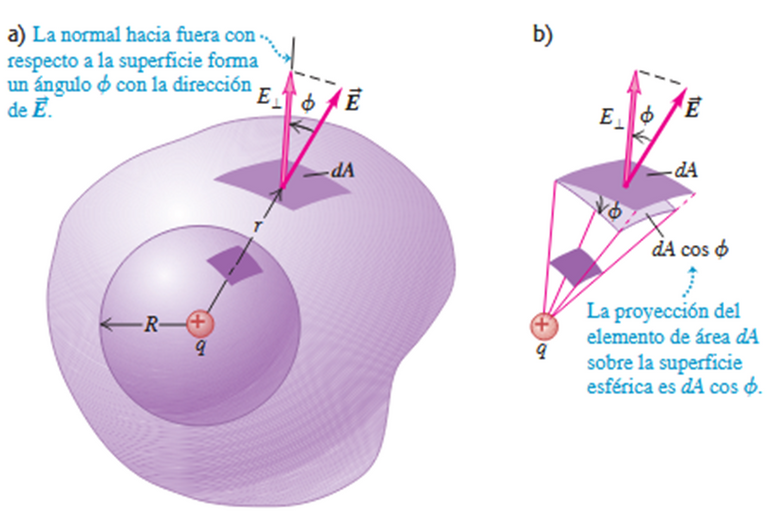
Fuente: Zemansky (2009)
Si dividimos la superficie irregular en elementos dA y calcular el flujo eléctrico E dA cos φ correspondiente a cada uno se podría sumar los resultado mediante una integración. Cada elemento de área se proyecta sobre un elemento correspondiente de la superficie esférica. De esta manera, el flujo eléctrico total a través de la superficie irregular deberá ser igual que el flujo total a través de una esfera que resulta ser igual a q/ε0. Entonces, para una superficie irregular.
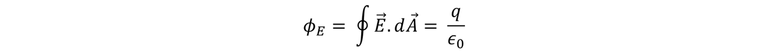
Dicha expresión es válida para una superficie de cualquier forma o tamaño, siempre y cuando cumpla con la única condición de que sea cerrada y encierre una carga q. El círculo que se puede apreciar sobre la integral nos refleja que se trata siempre de una superficie cerrada.
Algo que es muy importante considerar es que los elementos dA y los vectores unitarios siempre apuntan hacia afuera del volumen encerrado. Así que, el flujo eléctrico es positivo en las regiones donde el campo eléctrico apunta hacia afuera de la superficie y negativo donde apunta hacia adentro. De igual forma E ┴ es positivo en los puntos donde E apunta hacia afuera respecto a la superficie y negativo en los puntos donde apunta hacia adentro de la superficie.
También debemos tener en cuenta que si la carga puntual es negativa, entonces el campo E está dirigido en formal radial hacia adentro, por lo que el ángulo es mayor de 90º, su coseno es negativo y la integral es negativa, aunque q es negativa la ecuación seguirá siendo válida.
Para una superficie cerrada que no encierra carga alguna, la expresión es:
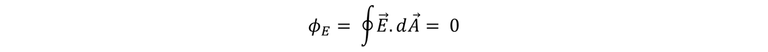
Dicho enunciado matemático que nos dice que cuando no existe carga, las líneas de campo originadas por cargas eléctricas fuera de la región deben entrar por un lado y salir por otro. en conclusión ”las líneas de campo eléctrico pueden iniciar o terminar dentro de una región del espacio sólo cuando hay carga en esa región”.
Ahora nos encontramos en la etapa final de encontrar la expresión general de la Ley de Gauss, si suponemos que una superficie no sólo encierra una carga puntual sino que son varias cargas; entonces el campo eléctrico total en cualquier punto es la suma vectorial de los campos individuales. Sea Qenc la carga total encerrada por la superficie, sea además E el campo total en la posición del elemento de área superficial dA y sea E ┴ su componente perpendicular al plano de ese elemento. Todas esas condiciones se pueden escribir en una sola ecuación, con respecto a cada carga y su campo correspondiente, es decir el enunciado general de la ley de Gauss.
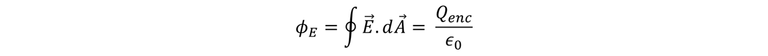
Y finalmente llegamos al enunciado de la ley de Gauss, Zemansky (Ob. Cit) lo describe de la siguiente manera, ” el flujo eléctrico total a través de una superficie cerrada es igual a la carga eléctrica total (neta) presente en el interior de la superficie, dividida entre ϵ_0.
Referencias
Figuera, J. (2009). Física, Texto y problemario. Caracas: Ediciones CO-BO.
Sánchez, E. (2005). Física. Caracas: Ediciones CO-BO.
Zemansky, S. (2009). Física Universitaria Volumen II. México: Pearson Educación.


0
0
0.000
https://twitter.com/ILovePhysica/status/1463632666134302722?s=20
https://twitter.com/ILovePhysica/status/1463632666134302722
The rewards earned on this comment will go directly to the person sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Su post ha sido valorado por @ramonycajal