Hablemos sobre Carga y Flujo Eléctrico
(Edited)
Casi siempre puede haber dos maneras de realizar una tarea, una manera por así decirla difícil y otra más sencilla, al igual que cuando queremos llegar a algún lugar, lo podemos hacer por el camino largo o simplemente tomar un atajo. En física, ocurre algo similar, y es que existe una herramienta muy útil que se puede utilizar con el fin de simplificar los problemas, y eso es el uso de las propiedades de simetría. Resulta que muchos sistemas físicos tienen simetría, un ejemplo común es un cilindro, el cual se ve exactamente igual después de hacerlo girar sobre su propio eje; lo mismo ocurre si una esfera metálica con carga se hace girar en torno al eje que pasa por su centro.

Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.
Es por ello, que la Ley de Gauss resulta ser una parte importante para simplificar los cálculos de campos eléctricos considerando la simetría. Por ejemplo, el campo de una lamina plana, el cual después de algunas integrales bastante trabajosas podríamos determinar. Pero la Ley de Gauss es algo más que un artificio matemático, esta Ley resulta ser un enunciado fundamental que nos habla sobre la relación entre las cargas eléctricas y los campos eléctricos, en conclusión nos ayuda a entender cómo se distribuye la carga eléctrica en los cuerpos conductores.
Analicemos la siguiente pregunta, “Dada una distribución de carga ¿Cuál sería el campo eléctrico que produce esa distribución en un punto P?” Si utilizamos el camino largo, podemos hallar una respuesta representando la distribución como un conjunto de cargas puntuales, entonces el campo total resultaría ser la suma vectorial de todos los campos debidos a todas las cargas puntuales.
Pero resulta, que existe otra relación entre las distribuciones de carga y los campos eléctricos. Para poder entender mejor esta relación, sería oportuno formular la pregunta nuevamente ”Si se conoce la disposición del campo eléctrico en una región especifica, ¿Qué se puede saber acerca de la distribución de carga en esa región?”.
Para responder esa pregunta analicemos la imagen que se presenta a continuación, se trata de una caja de un material que no influye en ninguno de los campos eléctricos. Supongamos que la caja representa una superficie imaginaria que puede encerrar o no cierta cantidad de carga, nos referimos a una superficie cerrada porque encierra totalmente un volumen, ¿Cómo podíamos saber cuánta carga hay dentro de la caja?
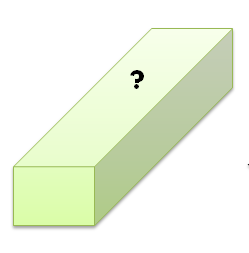
Algo debemos tener claro, y es que una distribución de carga produce un campo eléctrico y que un campo electico ejerce una fuerza sobre una carga de prueba. Podemos entonces, mover la carga en diversas posiciones dentro de la caja, luego de medir la fuerza eléctrica que la carga de prueba experimenta en distintas posiciones, podemos elaborar un diagrama del campo eléctrico E = F/Qo, tal como lo vemos en la siguiente imagen.
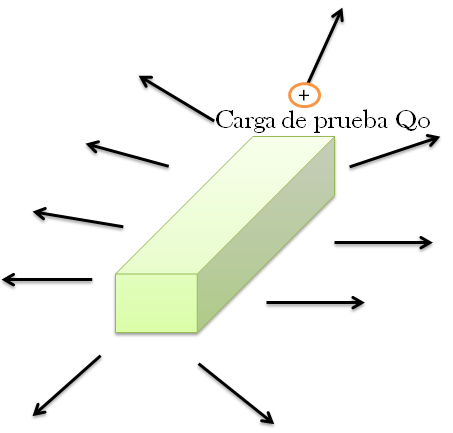
En dicho diagrama vemos el campo eléctrico que produce una carga eléctrica puntual positiva, ya con los detalles que suministra el diagrama podemos hallar el valor exacto de la carga puntual en el interior de la caja. Analicemos las siguientes imágenes:
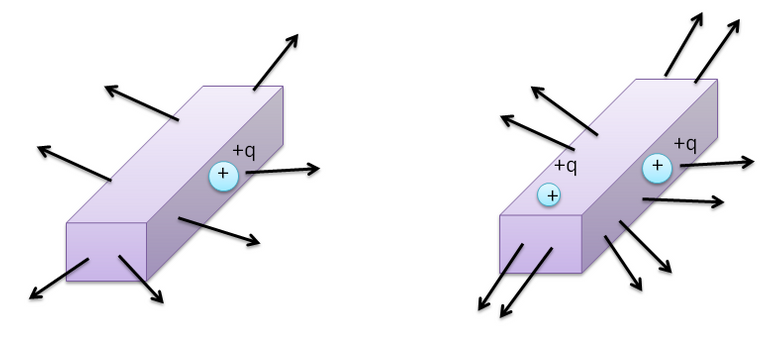
En la primera caja podemos observar una carga eléctrica puntual, mientras que en la segunda se encuentran dos cargas del mismo tipo; básicamente las disposiciones del campo son diferentes, pero algo tienen en común y es que ambas, bien sea con una o con dos cargas los campos apuntan hacia afuera de la caja.
Por otra parte, tenemos el caso contrario, una caja con una carga puntual negativa y la otra con dos cargas puntuales de igual forma negativas; igual los detalles del campo son diferentes, pero en ambos casos el campo apunta hacia adentro.
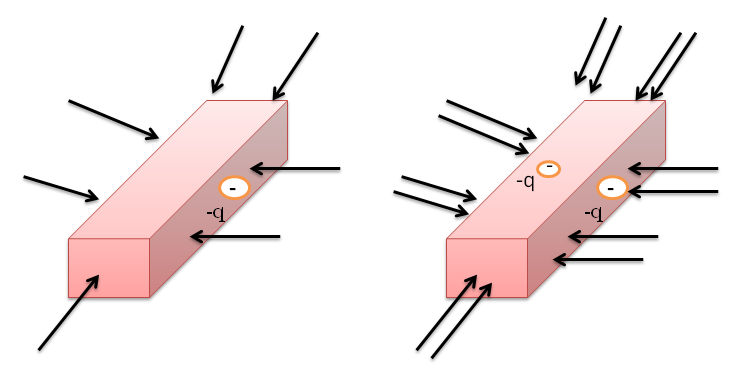
A pesar de que un campo eléctrico no “fluye” en realidad. Si podemos decir con base a lo observado que cuando los vectores de campo eléctrico apuntan hacia afuera de la superficie, estamos en presencia de un flujo eléctrico saliente. En donde los vectores del campo eléctrico apuntan hacia el interior de la superficie, entonces el flujo eléctrico es entrante.
Es decir, que la relación es sencilla, la carga positiva que se encuentra dentro de la caja atraviesa con un flujo eléctrico saliente la superficie de la caja, mientras que la carga negativa del interior lo hace con un flujo eléctrico entrante. Pero ya en este punto, puede surgir una interesante interrogante ¿Qué pasa si la carga que está dentro de la caja es cero? La respuesta es simple, la caja se encuentra vacía y el campo es cero en todas partes, por lo que, no hay flujo eléctrico ni hacia afuera, ni hacia dentro de la superficie.
¿Y qué pasaría si tuviésemos dos cargas dentro de una superficie de diferentes signos? Si ambas cargas son de igual magnitud, la carga neta dentro del interior de la caja es cero. Si existe un campo eléctrico, pero este fluye hacia afuera en la mitad de la caja y fluye hacia adentro en la otra mitad, por lo que no hay un flujo eléctrico neto hacia adentro o hacia afuera de la caja.
Una acotación que no podemos dejar pasar es que, no importa el tamaño de la superficie donde se encuentre la carga, el flujo eléctrico es directamente proporcional a la magnitud de la carga neta que encierra la caja. Es decir, es independiente del tamaño de la caja.
Ya para finalizar y después de haber tomado en cuenta varias situaciones podemos concluir que:
- Existe una relación entre la cantidad de carga neta dentro de una superficie cerrada y el flujo eléctrico a través de dicha superficie.
- El caso tal, en el que exista o no un flujo eléctrico saliente o entrante neto a través de una superficie cerrada depende únicamente del signo de la carga.
- Si una carga se encuentra afuera de la superficie cerrada no proporciona flujo eléctrico dentro de la superficie.
- Y por último, el flujo eléctrico neto es directamente proporcional a la cantidad de carga neta encerrada dentro de la superficie, no tiene ninguna relación con el tamaño de la superficie.
Referencias
Figuera, J. (2009). Física, Texto y problemario. Caracas: Ediciones CO-BO.
Sánchez, E. (2005). Física. Caracas: Ediciones CO-BO.
Zemansky, S. (2009). Física Universitaria Volumen II. México: Pearson Educación.


0
0
0.000
https://twitter.com/ILovePhysica/status/1451676309663387653?s=20
A very interesting topic but here is a problem that can be solved you have to use English also in the post! !discovery 20 Let's hope you take my recommendation hugs!
This post was shared and voted inside the discord by the curators team of discovery-it
Join our community! hive-193212
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program
Congratulations @hannymarchan!
You raised your level and are now a Minnow!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.