Equipotenciales y conductores
Resulta ser que existe una importante aseveración acerca de las superficies equipotenciales. El día de hoy estaremos hablando un poco sobre dichas aseveraciones, al igual que de otros tópicos necesarios en el estudio de potenciales eléctricos.

Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.
Algo súper importante de acotar es que cuando todas las cargas están en reposo, la superficie de un conductor es siempre una superficie equipotencial. Debido a que el campo eléctrico E siempre es perpendicular a una superficie equipotencial, se puede verificar este enunciado si se demuestra que cuando todas las cargas están en reposo, el campo eléctrico inmediatamente afuera de un conductor debe ser perpendicular a la superficie en todos los puntos.
Analicemos la imagen que se presenta a continuación y sabemos que E = 0 en todas las partes del interior del conductor; de lo contrario, las cargas se trasladarían. En particular, en cualquier punto precisamente adentro de la superficie la componente de E tangente a la superficie es cero. Se sigue que la componente tangencial de E también es cero casi afuera de la superficie. Si no lo fuera, una carga podría recorrer una trayectoria rectangular que estuviese en parte adentro y parte afuera y regresar al punto de partida habiéndose realizado una cantidad neta de trabajo sobre ella. Esto violaría la naturaleza conservativa de los campos electrostáticos; de este modo, la componente tangencial de E precisamente afuera de la superficie debe ser cero en todos los puntos de la superficie. Así, E es perpendicular a la superficie en todos los puntos, lo que prueba la aseveración.
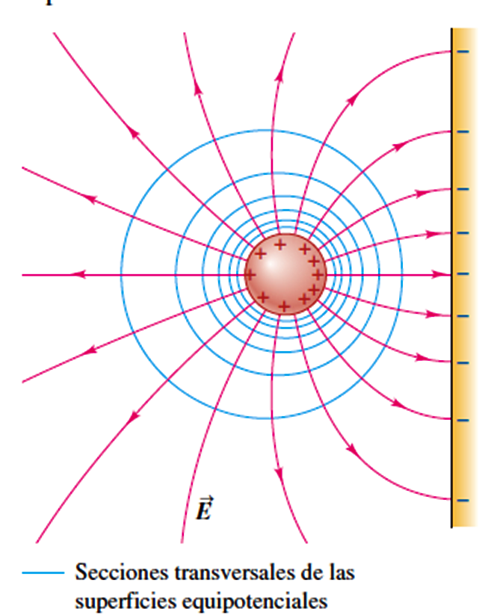
Fuente: Zemansky (2009)
Por otra parte, también se puede probar el siguiente teorema: en una situación electrostática, si un conductor contiene una cavidad y no hay carga en el interior de ésta, entonces no puede haber una carga neta en ninguna parte de la superficie de la cavidad. Esto significa que si uno está adentro de una caja conductora con carga sin sufrir una descarga. Para verificar dicho teorema, primero es propicio demostrar que todos los puntos del interior de la cavidad están al mismo potencial, en la imagen que se muestra seguidamente podemos observar una superficie conductora A de la cavidad es una superficie equipotencial, como recién hemos hablado. Suponiendo que el punto P de la cavidad está a un potencial diferente; por lo tanto se puede construir una superficie equipotencial diferente B que incluya al punto P.
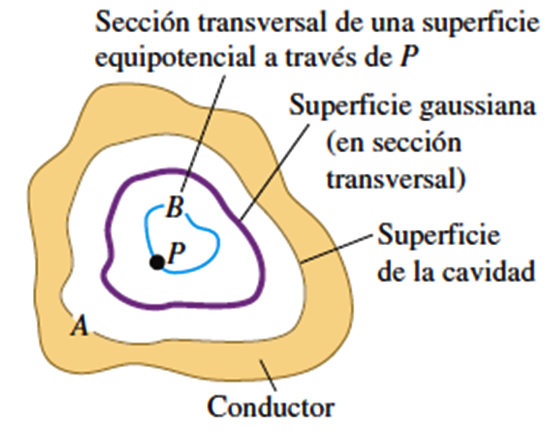
Fuente: Zemansky (2009)
Consideremos ahora una superficie gaussiana entre dos superficies equipotenciales. En virtud de la relación entre E y las equipotenciales, sabemos que en todos los puntos entre las equipotenciales el campo se dirige de A hacia B, o bien en todos los puntos se dirige de B hacia A, según la superficie equipotencial que esté al potencial más elevado. En uno u otro caso el flujo a través de esta superficie gaussiana es con certeza diferente de cero. Pero entonces la ley de Gauss afirma que la carga encerrada por la superficie gaussiana no puede ser cero. Esto contradice nuestra suposición inicial de que no hay carga en la cavidad. Por tanto, el potencial en P no puede ser diferente del que hay en la pared de la cavidad.
En consecuencia, la región de la cavidad en su totalidad, debe estar al mismo potencial. Sin embargo, para que esto sea cierto, el campo eléctrico en el interior de la cavidad debe ser cero en todas partes. Por último, la ley de Gauss demuestra que el campo eléctrico en cualquier punto de la superficie de un conductor es proporcional a la densidad de carga superficial σ en ese punto. En conclusión la densidad de carga superficial en la pared de la cavidad es cero en todos los puntos.
Finalmente, es importante acotar que no se debe confundir las superficies equipotenciales con las superficies gaussianas. Las superficies gaussianas son pertinentes solo cuando se utiliza la ley de Gauss y se puede elegir cualquier superficie gaussiana que resulte conveniente. No podemos elegir libremente la forma de las superficies equipotenciales, su forma está determinada por la distribución de la carga.
Referencias
Figuera, J. (2009). Física, Texto y problemario. Caracas: Ediciones CO-BO.
Sánchez, E. (2005). Física. Caracas: Ediciones CO-BO.
Zemansky, S. (2009). Física Universitaria Volumen II. México: Pearson Educación.


0
0
0.000
https://twitter.com/ILovePhysica/status/1481059370582614017?s=20
https://twitter.com/ILovePhysica/status/1481059370582614017
The rewards earned on this comment will go directly to the person sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.