Diferencia de Potencial en función a una integral de E
(Edited)
Antes de comenzar con el desarrollo de un nuevo tema quiero desearles una 🎅 Feliz Navidad🎄. En la publicación anterior estuvimos desarrollando por primera vez el concepto de potencial eléctrico, el día de hoy tocaremos algunos puntos que la vez pasada no, así como algunos ejemplos prácticos.

Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.
Uno de los puntos que nos quedó pendiente de la publicación anterior fue el de potencial eléctrico cuando se tiene un conjunto de cargas puntuales, resulta que con las expresiones descritas anteriormente resulta ser ordinariamente el método más fácil para calcular el potencial V. Pero resulta que en ciertos problemas en el que se conoce el campo eléctrico o se puede hallar fácilmente, es más simple determinar V a partir de E. La fuerza F sobre una carga de prueba qo se puede definir como F = qoE, así que podemos deducir que el trabajo realizado por la fuerza eléctrica cuando la carga de prueba se desplaza de a hasta b e encuentra dada por:
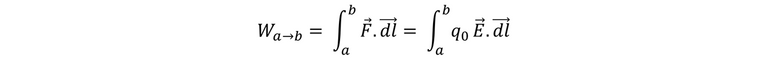
Y si dividimos toda la expresión entre qo obtenemos la diferencia de potencial como una integral de E.
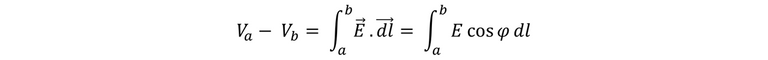
Cabe destacar que el valor de Va – Vb es independiente de la trayectoria seguido para ir de a hasta b, del modo que el trabajo es independiente de la trayectoria. Para poder interpretar la expresión anterior es importante recordar que E es la fuerza eléctrica por unidad de carga sobre una carga de prueba. Si la integral de línea es positiva, entonces el campo eléctrico realiza trabajo positivo sobre una carga positiva de prueba conforme ésta se desplaza de a hasta b. En dicho caso la energía potencial eléctrica disminuye a medida que la carga de prueba se desplaza, por lo que la energía potencial por unidad de carga también disminuye, y entonces Vb es menor que Va y Va – Vb es positiva.
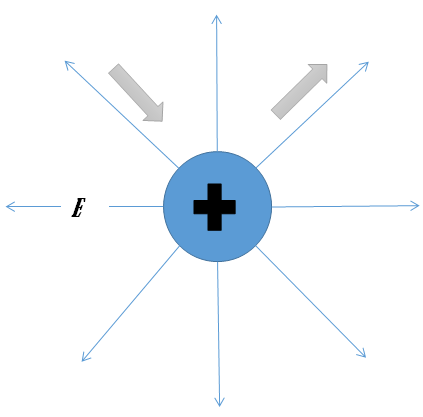
En la imagen que vemos a continuación se muestra una carga puntual positiva. En la misma la dirección del campo eléctrico se aleja de la carga y V = q/4πεₒr es positivo a cualquier distancia finita de ésta. Si nos alejamos de la carga, en la dirección de E nos desplazamos hacia valores más pequeños de V; si nos acercamos a la carga, en la dirección opuesta a E, avanzamos hacia valores más grandes de V.
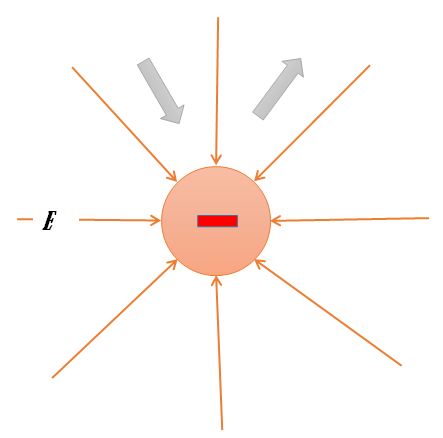
Ahora veamos la siguiente imagen, donde tenemos una carga puntual negativa. En este caso vemos que el campo eléctrico está dirigido hacia la carga y V = q/4πεₒr es negativo a cualquier distancia finita de ésta. En este caso si nos desplazamos hacia la carga. Lo hacemos en dirección de E y en la dirección de V decreciente. Al alejarnos de la carga, en la dirección opuesta a E, nos desplazamos hacia valores crecientes de V. La regla general, válida para cualquier campo eléctrico, es: desplazarse en la dirección de E significa avanzar en la dirección de V decreciente, y desplazarse contra la dirección de E significa avanzar en la dirección de V creciente.
Por otra parte, una carga positiva de prueba qo experimenta una fuerza eléctrica en la dirección de E hacia valores más pequeños de V, una carga negativa de prueba experimenta una fuerza opuesta a E, hacia valores más grandes de V. De esta manera, una carga positiva tiende a caer de una región de potencial elevado a una de potencial más bajo. Caso contrario sucede cuando la carga es negativa.
Es decir, que la relación de diferencia de potencial como integral de E, también se puede escribir de la siguiente manera:
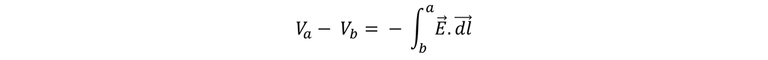
Si observamos bien esta expresión podemos notar que en comparación con la ecuación anterior aquí hay un sigo negativo y los límites de integración están invertidos por lo tanto las ecuaciones son equivalentes. Claro es importante acotar que esta ecuación tiene una interpretación un poco diferente. Para desplazar lentamente una carga unitaria contra la fuerza eléctrica, es preciso aplicar una fuerza externa por unidad de carga igual a -E, igual y opuesta a la fuerza eléctrica por unidad de carga E. También podemos afirmar que Va – Vb = Vab, el potencial de a con respecto a b. es igual al trabajo por unidad de carga realizado por esta fuerza externa para desplazar una carga unitaria de b hasta a.
Finalmente, las ecuaciones anteriores muestran que la unidad de diferencia de potencial (1V) es igual a la unidad de campo eléctrico (1 N/C) multiplicada por la unidad de distancia (1 m). Por lo tanto, la unidad de campo eléctrico se puede expresar como 1 voltio por metro (1 V/m) o como 1 N/C:
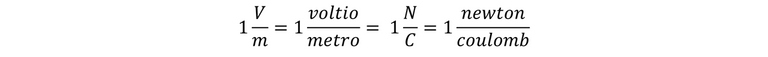
Generalmente la unidad más utilizada de campo eléctrico es voltio por metro. Cabe resaltar, que la magnitud de e de la carga del electrón permite definir una unidad de energía que resulta ser útil en muchos cálculos de sistemas atómicos y nucleares. Cuando una partícula con carga q se desplaza de un punto donde el potencial es Vb a un punto donde es Va, por lo que el cambio de energía potencial U es:
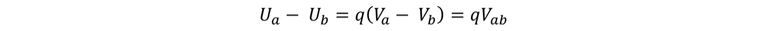
Si la carga q es igual a la magnitud e de la carga del electrón,
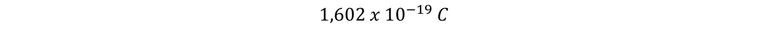
Y la diferencia de potencial es Vab = 1 V, por lo que el cambio de energía es:
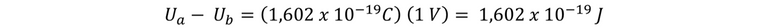
A esta cantidad de energía se le define como 1 electrón voltio (1 eV):
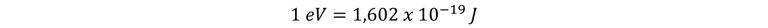
Referencias
Figuera, J. (2009). Física, Texto y problemario. Caracas: Ediciones CO-BO.
Sánchez, E. (2005). Física. Caracas: Ediciones CO-BO.
Zemansky, S. (2009). Física Universitaria Volumen II. México: Pearson Educación.


0
0
0.000
https://twitter.com/ILovePhysica/status/1474872446578827266
The rewards earned on this comment will go directly to the person sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
https://twitter.com/ILovePhysica/status/1474872446578827266?s=20
Su post ha sido valorado por @goya
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Hola @hannymarchan muy clara la explicación de la diferencia de potencial en función de E. Asuntos de mucho interés para comprender este mundo de la electricidad. Gracias