¿Cómo podemos calcular el flujo eléctrico?
En la publicación anterior conocimos un poco sobre el flujo eléctrico en términos teóricos, observamos diferentes casos de cuando tenemos una carga eléctrica dentro de una superficie cerrada, pero ¿Cómo podemos determinar el flujo eléctrico? Responderemos esta pregunta a lo largo de esta publicación.
Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.
Como ya sabemos, el flujo eléctrico es una descripción de si el campo eléctrico apunta hacia afuera o hacia adentro, y en base a esto pudimos llegar a la conclusión de que “el flujo eléctrico neto a través de una superficie cerrada es directamente proporcional a la carga neta en el interior de esa superficie”. Ahora bien, es propicio saber cómo calcular dicho flujo eléctrico, y es necesario que utilicemos nuevamente la analogía entre un campo eléctrico E y el campo de vectores de velocidad v de un fluido en circulación, aunque hay que hacer énfasis que se trata de una analogía, ya que el campo eléctrico no es un flujo.
Es momento de visualizar la siguiente imagen, la cual trata un fluido que fluye de manera uniforme de izquierda a derecha, si examinamos la relación de flujo volumétrico dV/dt a través del rectángulo de alambre de área A.
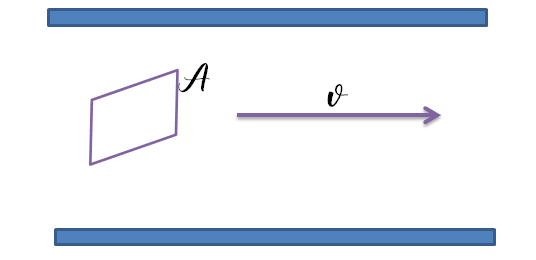
Cuando dicha área es perpendicular a la velocidad de flujo y la velocidad de flujo es la misma en todos los puntos del fluido, entonces la relación de flujo volumétrico dV/dt es el área A multiplicada por la rapidez de flujo:
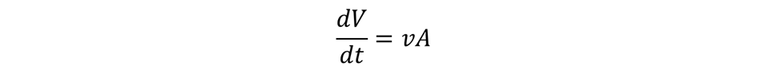
Si tomamos el rectángulo de la imagen anterior y lo inclinamos un poco, más o menos a un ángulo ϕ de modo que su cara no sea perpendicular a v, el área que vamos a considerar es la que se forma con la silueta que logramos visualizar cuando enfrentamos la dirección de v, para este caso la relación de flujo volumétrico a través de A es
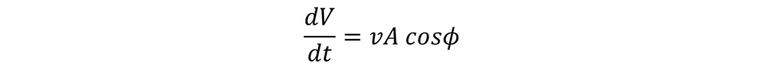
Si ϕ = 90º, dV/dt = 0; Asimismo, v cosϕ es la componente del vector v la cual es perpendicular al plano del área A, dicha componente la podemos escribir en base a la relación de flujo volumétrico de la siguiente manera:
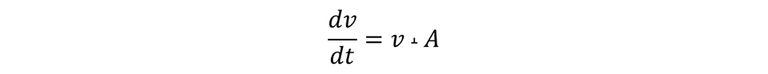
La relación de flujo volumétrico se puede expresar de manera más simple utilizando el concepto de vector área, A, una magnitud vectorial de magnitud A y dirección perpendicular al plano del área. No obstante, el vector de área A relaciona tanto el tamaño de un área como su orientación en el espacio. En relación a A, entonces podemos escribir el flujo volumétrico de fluido a través de un rectángulo como:
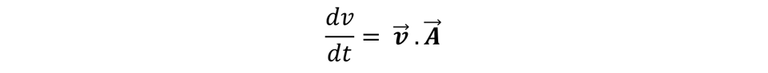
Si hacemos uso de la analogía que existe entre el campo eléctrico y el flujo de fluidos, podemos definir el flujo eléctrico de la misma manera que un flujo volumétrico; para ello sustituimos la velocidad del fluido v por el campo eléctrico E. Primeramente consideremos un área plana A perpendicular a un campo eléctrico uniforme E como lo podemos ver en la imagen siguiente.
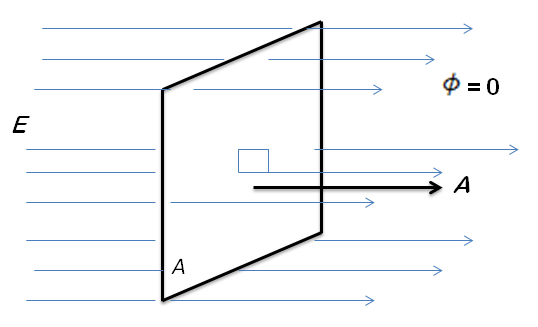
Se puede definir el flujo eléctrico a través de esta área como el producto de la magnitud del campo E por el área A:
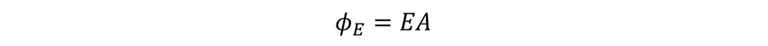
Ahora bien, podemos escribir ϕ_E en términos de las líneas de campo que pasan a través de A. Si aumentamos el área, entonces las líneas de campo que atraviesan aumentan, por lo tanto, aumenta el flujo; un campo más intenso significa tener líneas de campo más cercanas unas a otras y, por tanto, más líneas en cada unidad de área, de modo que el flujo aumenta.
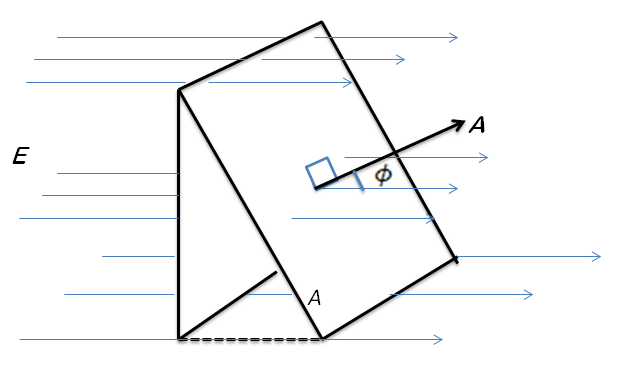
Ahora analicemos otra situación, si tenemos un área A que es plana pero no perpendicular al campo E, entonces la atraviesan menos líneas. Visualicemos la imagen que sigue, en este caso se considera el área de a silueta que podemos ver cuando se enfrenta la dirección de E.
Esta es el área A y es igual a Acosϕ, el cual lo podemos definir como
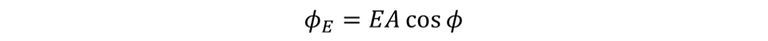
Como Ecosϕ es la componente de E, la cual es perpendicular al área y se puede volver a escribir de la manera siguiente:
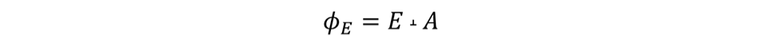
También podemos escribir el vector en términos de un producto escalar como:
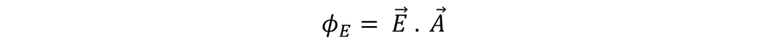
Toda las ecuaciones anteriores expresan diferentes modos, aunque equivalentes, el flujo eléctrico correspondiente a una superficie plana y a un campo eléctrico uniforme. Si observamos la imagen que se presenta a continuación, donde el campo E y A son perpendiculares, el flujo es cero.
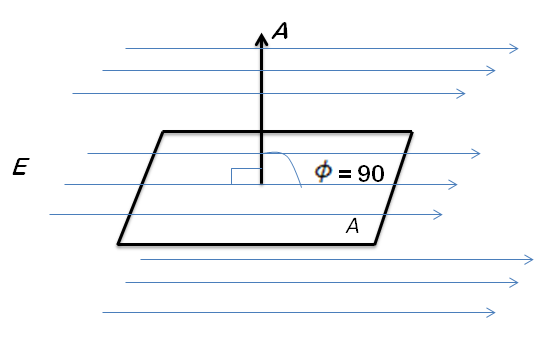
Por lo que
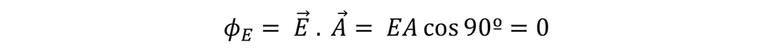
Referencias
Figuera, J. (2009). Física, Texto y problemario. Caracas: Ediciones CO-BO.
Sánchez, E. (2005). Física. Caracas: Ediciones CO-BO.
Zemansky, S. (2009). Física Universitaria Volumen II. México: Pearson Educación.


0
0
0.000
https://twitter.com/ILovePhysica/status/1457852814777065481?s=20
https://twitter.com/ILovePhysica/status/1457852814777065481
The rewards earned on this comment will go directly to the person sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
Su post ha sido valorado por @ramonycajal
Hola, @hannymarchan presentas casos que logran entenderse. Ojo, no porque de alguna forma estoy involucrado en este campo. Realmente, la soltura es magnífica. El electromagnetismo siempre ha sido un paso crucial en el entendimiento de este campo. Gracias.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.