Teoría de Probabilidad como Estrategia Matemática en el Analisis de Decisión

Por tal razón, las matemáticas es una herramienta clave para la identificación de las decisiones más acertadas. Además, existe una serie de estrategias, donde los métodos cuantitativos juegan un papel significativo, cabe destacar que una de las técnicas más utilizadas es el análisis de decisión con la teoría de probabilidad, ya que la misma es una rama de las matemáticas, que se utiliza normalmente para expresar algún acontecimiento relevante o de un evento que tiene una naturaleza incierta.
Sin embargo, a pesar del buen desarrollo que se tenga para las decisiones, algunas probablemente resulten equivocadas. Si bien es cierto las circunstancias cambian y la decisión que era apropiada hace 6 meses ya no es válida para la fecha. Como consecuencia, de la decisión equivocada se obtiene beneficios porque siempre se aprende de los errores, es ahí donde la experiencia de los decisores los lleva a hacer una jugada inteligente sobre lo que pueda pasar, siendo utilizada la teoría de probabilidad en el análisis final de la decisión. Aunque es un concepto muy familiar exige considerar la naturaleza matemática del mismo. Sin embargo, en los modelos probabilísticos, el gerente no se preocupa por los resultados, sino por la cantidad de riesgos que cada decisión arrastra, cualquier circunstancia puede influir y cambiar el futuro, ya que tiene un elemento de incertidumbre.

El proceso para manejar el riesgo y la incertidumbre es parte de cualquier modelo probabilístico, ya que la ocurrencia de un determinado suceso es la proporción de veces que ocurre dicho suceso, siendo el factor más importante en la determinación de un modelo de decisión de implementación exitosa. La teoría de probabilidad constituye la base del llamado análisis bayesiano. Por lo tanto, a priori no se conoce cuál de los resultados se va a presentar. Por ejemplo si nos vamos con el juego de las monedas al lanzamiento al aire, sabemos que el resultado o puede ser cara o bien sello, pero antes del lanzamiento no sabemos a ciencia cierta cuál va a ser el resultado. En un principio se estudia el problema, luego se desarrolla el modelo matemático, que se combina información sobre probabilidades. Por lo tanto, la evaluación de riesgo significa un estudio para determinar los resultados de las decisiones junto a sus probabilidades.

Además, las acciones están basadas en los resultados esperados, que se mueve desde un modelo determinístico a probabilístico. Es fundamental que los experimentos sean aleatorios, porque si no son aleatorios no se les puede aplicar las reglas de la probabilidad, esto significa que en lugar de lanzar la moneda de una hacemos la selección de la cara donde está el sello en este caso no aplica la teoría de probabilidades, pueden presentarse diversas consecuencias, dentro de un conjunto posible de soluciones. A partir de allí, las consecuencias de las elecciones, afrontan las decisiones como si fueran apuestas, es decir, debe calcularse la utilidad, la probabilidad de opciones, para establecer estrategias y aplicar una buena toma de decisiones.

Por su parte, la elección entre acciones posibles, y la predicción de resultados esperados resultan del análisis lógico que el gerente hace de la situación de decisión. Sin embargo, la teoría de la decisión se hace cálculos del valor de un cierto resultado y sus probabilidades. Generalmente, las probabilidades se ven expresadas en decimales, porcentajes o fracciones, cada experimento aleatorio tiene definido el conjunto con todas las soluciones posibles conocido normalmente como espacio muestral, es decir si lanzamos una moneda al aíre, se pueden generar varias opciones o bien sea cara o sello, ahora si el lanzamiento de la moneda se realiza dos veces, entonces el conjunto de posibles soluciones seria:
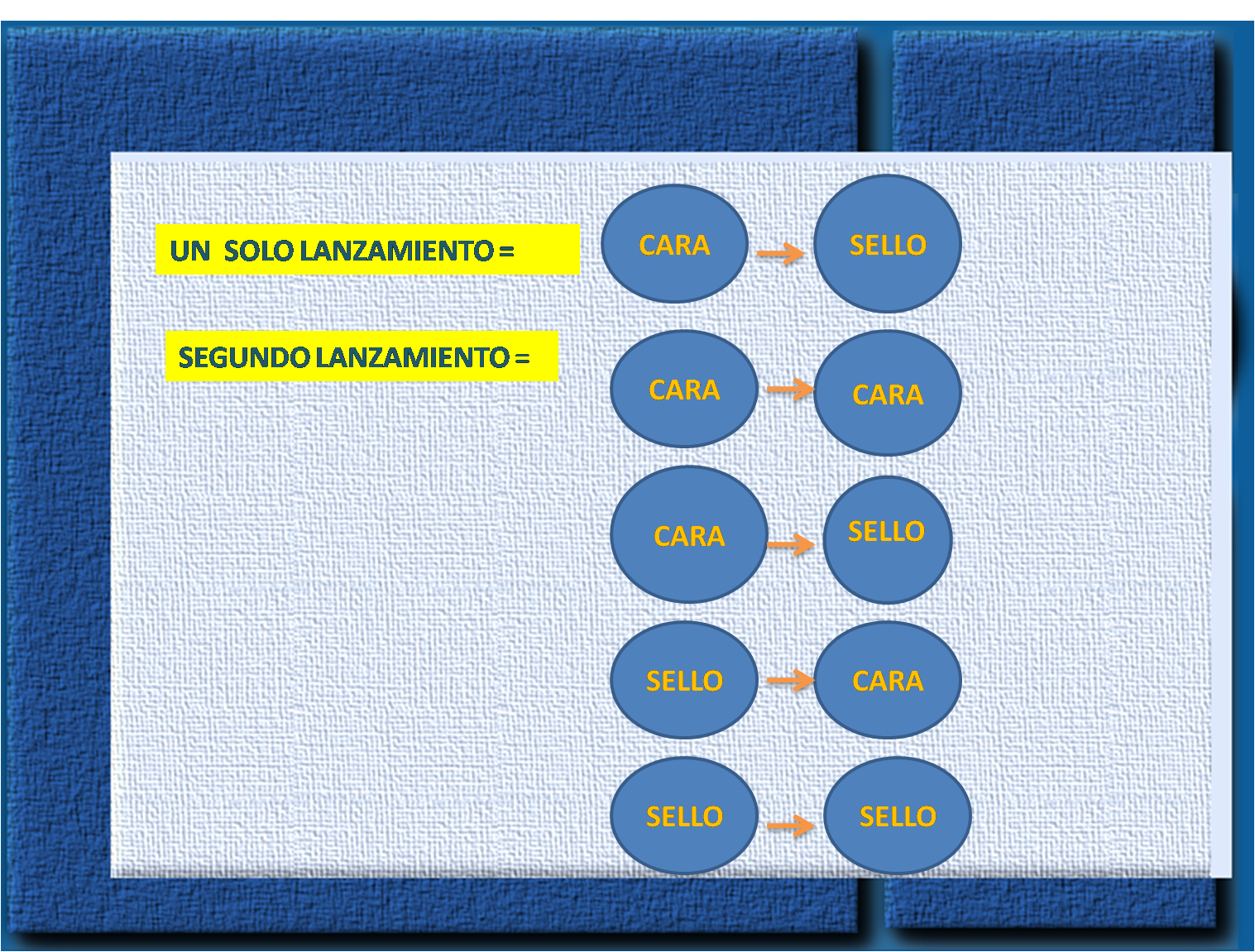
En las decisiones tomadas con incertidumbre, el decisor no tiene ningún conocimiento, el tomador de decisiones debe analizar los escenarios, el decisor se basa en su actitud hacia la incógnita, ni siquiera de la probabilidad de ocurrencia de cualquier estado de la naturaleza. Es importante, explicar que la probabilidad se mide por un número entre cero y uno: si un experimento no ocurre nunca, su probabilidad es cero, mientras que si ocurriese siempre su probabilidad sería igual a uno. Así, por ejemplo, en un hospital geriátrico hay 50 pacientes hospitalizados, de los cuales 5 tiene Alzheimer, la probabilidad de padecer Alzheimer, se estimará como el cociente es decir 5/50= 0,1. Es decir que el 0,1 tiene la probabilidad de contraer Alzheimer en ese centro hospitalario.
Para conocer bien o hacer un análisis de decisión adecuado a través de la probabilidad hay que tener en cuenta varias formulas que son muy sencillas y fáciles de entender:

Otra de las formulas aplicables de la teoría de probabilidades para los decisores es cuando un fenómeno determinado tiene dos posibles resultados A y B mutuamente excluyentes, que quiere decir con esto, que no pueden suceder de forma simultánea, Para explicar este caso vamos a seguir con el ejemplo del lanzamiento de las monedas que es bastante sencillo y entendible para todos. Por tal razón, para conocer la probabilidad de que una de las dos posibilidades ocurra, solo debemos hacer una operación matemática de suma de las dos probabilidades:

Consideremos, como ejemplo, En un servicio donde se practica estudios de biopsias de personas que tienen cáncer en el colon se puede decir en que está representada por un 42,2% de los pacientes presentan su biopsia negativa es decir benigna (BN), el 21,2% positiva pero Benigna (PB) y en un 36.6% el diagnóstico es lamentablemente positivo de que las personas tienen cáncer en el colon (PC). Ahora el análisis de decisión parte de la probabilidad de que en un paciente que se somete a una biopsia no se confirme el diagnóstico de cáncer en el colon a través de la siguiente fórmula:

Ahora podemos hacer un analisis de decisición con el ejercicio anterior en la probabilidad del caso contrario, es decir cuando el diagnostico es de cancer.

Por lo tanto, si un fenómeno determinado tiene dos posibles resultados A y B, la probabilidad de que una de las dos posibilidades suceda viene dada, por la expresión:

Existen diversos sucesos o eventos en las probabilidades. En ocasiones el hecho de que se produzca un determinado fenómeno puede hacer más o menos probable la aparición de otro. Estos son Probabilidades Condicionadas.
Supongamos, con un ejemplo, que queremos estudiar la incidencia del hecho de las personas con Anzheimer como factor de riesgo en las personas de la tercera edad en una determinada población. Para ello se diseñó un estudio y se selecciono una muestra de 150 usuarios. A continuación se muestra una tabla con los siguientes datos.
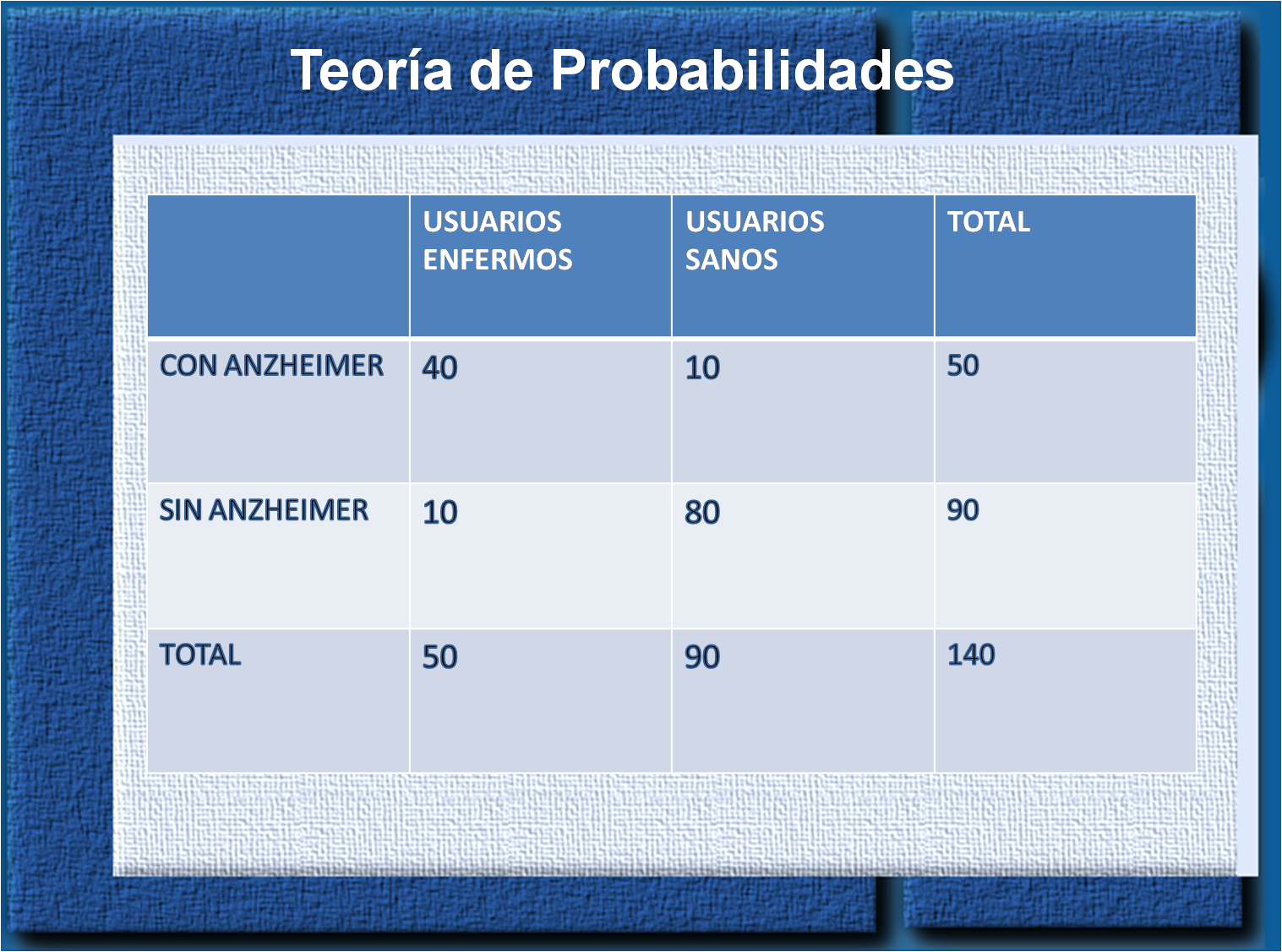
Considerando toda la muestra, la probabilidad de desarrollar Anzheimer en la población de estudio es:


Conclusión:
Hoy en día gracias a las matemáticas, y las implicaciones que tiene en la toma de decisiones en las organizaciones nos permite cumplir satisfactoriamente con la dinámica de los diversos sistemas administrativos, ya que el análisis de decisión se enfoca en los factores de la actitud psicológica del decisor y en su entorno más relevante, ya que le permite examinar el riesgo dentro de su retorno esperado, e identificar aspectos críticos, ya que un evento inesperado con consecuencias significativas arrojaría riesgos o oportunidades. De ahí nacen las buenas decisiones donde se requiere buscar un conjunto de alternativas, porque no sabemos realmente donde está el problema que nos limita a lograr el éxito. Siendo la teoría de probabilidades la herramienta principal para comunicar y manejar la incertidumbre, ya que el cálculo de probabilidades constituye una herramienta que permitirá hacer inferencia sobre distintos parámetros poblacionales a partir de los resultados obtenidos de una muestra, y después tomar decisiones con el mínimo riesgo de equivocación en situaciones de incertidumbre
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Thanks for using the STEMsocial app, which gives you stronger support. Including @stemsocial as a beneficiary could yield even more support next time.