♾ π Ramanujan sigue conociendo al infinito con nuevas conjeturas
♾ π Ramanujan sigue conociendo al infinito con nuevas conjeturas
Por Enio...
¿Quién ha sido el más talentoso matemático de la historia? Es una pregunta para la cual no podríamos tener un respuesta a ciencia cierta, pero de alguna manera tenemos indicios que nos ayudan a proponer los más claros contendientes, tal como pasa en el ajedrez, en donde los nombres José Raul Capablanca y Paul Morphy nunca quedarán fuera de la lista de candidatos.
Quizá uno de los más fuertes contendientes para el título del matemático más talentoso haya sido Srinivasa Ramanujan, un auténtico genio indio a quien perdimos prematuramente (falleció a los 32 años), pero que en su corta vida y con formación meramente autodidacta asombró a sus colegas europeos profesionales y peso pesado con su arsenal de miles de ideas y ecuaciones y, en especial, con su prolífica capacidad para el descubrimiento -casi que por improvisación- de conjeturas matemáticas.
Sobre él conozco una película llamada El hombre que conocía el infinito (2015) que forma parte de mi colección de películas STEM y que desde luego les recomiendo. Esta relata parte de su vida y de sus esfuerzos por educarse formalmente y hacer carrera en el seno de la sabiduría contemporánea europea, para lo cual sufrió mucha discriminación de parte de una sociedad conservadora y eurocéntrica, aunque eventualmente logró un decente reconocimiento.

⬆️ Imagen 1: Srinivasa Ramanujan, un auténtico prodigio indio para las matemáticas.

⬆️ Imagen 2: Póster de la película El hombre que conocía el infinito. Si quieres aprender más sobre este genio y sus aportes, observa la película y lee un poco más sobre él.
El nombre de Ramanujan siempre sale a la palestra entre los matemáticos académicos, pero más recientemente vuelve a ser recordado gracias a una investigación publicada en la revista Nature que apunta al desarrollo de un sistema informático con la capacidad de autogenerar conjeturas a partir de constantes matemáticas.
Se trata, una vez más, de la aplicación de la inteligencia artificial para repotenciar y acelerar la investigación en distintos campos, en este caso las matemáticas, incluso si ello implique sustituir a los seres humanos en tamaña empresa del reino del razonamiento.
Los algoritmos bautizados como Ramanujan Machine (la Máquina de Ramanujan), en claro homenaje al genio indio, pretenden alimentar un ámbito de investigación matemático en el cual existe un progreso relativamente lento, pues la mayoría de los matemáticos y científicos de la computación de esta área se enfocan en probar los teoremas más que en descubrirlos. Se trata de dos campos de investigación relacionados pero contrapuestos, y la balanza no favorece al lado del descubrimiento. Ello es así porque hallar nuevos teoremas es una labor ardua y a menudo depende de la esporádica aparición de figuras como el mismo Ramanujan y la prodigiosa intuición de estas personas.
Recordemos que las conjeturas son conclusiones matemáticas que probablemente resulten ser ciertas, pues nunca se consiguen inconsistencias en ellas (hacerlo las refutaría), pero que a pesar de ello no han sido probadas rigurosamente, esto es, carecen de demostración. La conjetura posiblemente más famosa es el Último teorema de Fermat que afirma que no existen tres enteros positivos que puedan resolver la ecuación an + bn = cn.
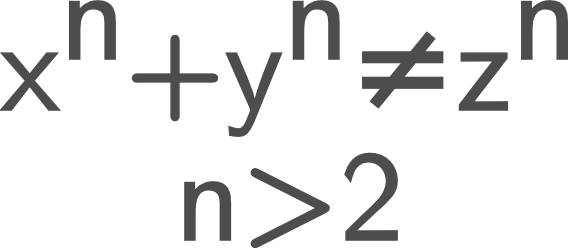
⬆️ Imagen 3: Último teorema de Fermat. Se ve sencillo, pero su consistencia es perfecta y nadie tiene idea de cómo probarlo o refutarlo. La intución para concebirlo ha sido extraordinaria.
Entonces, ¿debemos esperar que la naturaleza y el azar nos envíen estos genios improbables cada cierto tiempo para poder avanzar? Gracias a la inteligencia artificial estamos acortando la espera.
En este sentido, la clave del enfoque de la Máquina de Ramanujan radica exclusivamente en el uso de constantes matemáticas como base para la generación de las conjeturas; constantes como el famoso π, que es el cociente del radio de una circunferencia con respecto su diámetro, un inagotable e inmutable número que aprendemos desde el bachillerato, pero que ya era conocido por la humanidad desde la época del antiguo Egipto. Sabemos que estas constantes son universales y omnipresentes, por lo que se encuentran traducidas en distintos fenómenos naturales físicos, químicos y biológicos, así como también en la geometría y las matemáticas abstractas.
⬆️ Imagen 4: Algunas constantes matemáticas bien conocidas.
De tal manera que, metafóricamente, se trata de un poderoso conjunto de ingredientes para la producción de incontables derivados. Al seguir esta metodología, que no depende de conocimientos previos ni retroalimentación sino solamente las combinación de las constantes siguiendo un conjunto de reglas, las posibilidades de nuevas conjeturas podrían ser infinitas.
El sistema ya ha sido capaz de producir "docenas" de conjeturas, muchas de las cuales ya habían sido descubiertas anteriormente, las cuales incluye varias de fácil demostración, confirmando así la capacidad del sistema para producir conjeturas válidas, pero también ha producido conjeturas que están por demostrar, lo que incluye el descubrimiento de originales formas fraccionarias de calcular la constante π.
Las buenas noticias no acaban allí, ya que según el artículo científico publicado, los algoritmos están permitiendo especialmente el descubrimiento de una "nueva estructura algebraica oculta en la constante de Catalán", lo que sugiere que la Máquina de Ramanujan podría ser capaz de producir avances reales que el mundo de las matemáticas totalmente inéditos, algo que mantiene entusiasmado a los investigadores quienes añaden: "Creemos y esperamos que las pruebas de nuevas conjeturas generadas por ordenador sobre las constantes fundamentales ayudarán a crear conocimiento matemático".
Sobre la verdad o falsedad de los teoremas, no es responsabilidad de la Máquina de Ramanujan demostrar, pues, como se dijo, la contribución de esta investigación es hacia la generación automatizada de teoremas. Probarlos sería trabajo para los matemáticos humanos, y de la misma manera como el verdadero Ramanujan dejó numerosas conjeturas de gran elegancia y funcionalidad, muchas aún están esperando por demostración y puede que nunca podamos lograrlo.
Recordemos que la generalización de los teoremas de la incompletitud de Gödel nos permite deducir que hay ciertas afirmaciones matemáticas las cuales, a pesar de su consistencia, no podrán ser probadas y menos si el método empleado es algorítmico, lo cual no deja de ser paradójico considerando que la Máquina de Ramanujan es 100% algorítmica.
En cualquier caso, la máquina de Ramanujan es un paso en la dirección correcta y abona el terreno para nuevas investigaciones. Podremos encontrar varios de los teoremas descubiertos por los algoritmos en el sitio web RamanujanMachine.com que los autores han habilitado. Incluso, los investigadores aspiran construir una comunidad para lo cual han puesto el software a disposición. Los usuarios pueden contribuir con el proyecto al aportar poder de procesamiento. Sí, tú y tu computadora pueden ser partícipe en el descubrimiento de nuevos teoremas matemáticos como lo hacía Ramanujan, el hombre que conoció el infinito.
ALGUNAS REFERENCIAS
- Raayoni, G., Gottlieb, S., Manor, Y., Pisha, G., Harris, Y., Mendlovic, U., ... & Kaminer, I. (2021). Generating conjectures on fundamental constants with the Ramanujan Machine. Nature, 590(7844), 67-73 Versión en inglés.
- Las demás fuentes se incoporan en el texto del artículo.
- La imagen 1 es de los repositorios de Wikimedia commons. Fuente
- La imagen 2 está entre los repositorios de Wikimedia commons y puede ser utilizada por terceros. Fuente
- La imagen 3 es de los repositorios de Wikimedia commons. Fuente
- La imagen 4 es de Luckyman y es de licencia CC. Fuente
- A menos que se indique lo contrario, las imágenes son del autor o son de dominio público.
Si estás interesado en más temas sobre Ciencia, Tecnología, Ingeniería y Matemáticas (STEM, siglas en inglés), consulta las etiquetas #STEM-Espanol y #STEMSocial, donde puedes encontrar más contenido de calidad y también hacer tus aportes. Puedes unirte al servidor de Discord de STEM-Espanol para participar aún más en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol.
NOTAS ACLARATORIAS



Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a usar nuestra etiqueta ENLACE y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
¿QUIERES AUTOMATIZAR TUS GANANCIAS DE CURACIÓN? SE PARTE DEL PROYECTO ENLACE APOYANDO A NUESTRO TRAIL EN HIVE.VOTE INGRESA AQUÍ PARA CONCOCER LOS DETALLES.
¿QUIERES INVERTIR ENLACE? DESCUBRE COMO HACERLO Y GENERAR INGRESOS DE FORMA SEMANAL MEDIANTE TU DELEGACIÓN DE HP AQUÍ TE EXPLICAMOS COMO.
Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS
Atentamente
EQUIPO ENLACE 2021
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Thank you! :)
Is this the great Indian Mathematician Sir. Ramanujan.. I happen to see one of his documentaries and just loved it. cheers
Awesome. Yes, it's him!
Congrats, you were upvoted from this account because you were in Top 25 engagers yesterday on STEMGeeks .
You made a total of 2 comments and talked to 2 different authors .
For more details about this project please read here - link to announcement post
You can also delegate and get weekly payouts.
Thank you so much!
You are most welcome @eniolw . Keep up the good work and engage more to earn more.