THE PHYSICS BEHIND OSCILLATIONS AND MECHANICAL WAVES

The most powerful natural mechanical waves, and so potentially the most devastating, are those caused by earthquakes. They are called seismic waves from the Greek word seismos which means a shaking. Earthquakes can occur almost anywhere in the world, though fortunately there are no major ones in Britain.

Severe earthquakes occur close to fault lines in the Earth’s crust. Architects and engineers go to great lengths to protect buildings and other structures. They add strength by using more steel and more concrete than is usual elsewhere. They also introduce mechanical damping, putting rubber inserts or even metal springs into the supports.

An object, a bell for instance, can have a natural frequency at which it resonates. So can the walls of a room and even a whole building. Seismic waves at the natural frequency of a building would cause it to oscillate wildly and then collapse, so architects make sure that buildings do not have natural frequencies in a range that would make them vulnerable.

Preventing a high-rise building from toppling is difficult enough, but stopping the collapse of flyovers has proved particularly tricky, as highway engineers in Japan and California have discovered after major earthquakes which have caused chaos and death. California, in particular, awaits the ‘big one’ - a massive earthquake along the San Andreas fault line which it is predicted could occur in the next few years.

^{Ikluft, CC BY-SA 4.0}

The ideas in this chapter

As the chapter opener indicates, the study of oscillations and mechanical waves is of crucial importance to our everyday safety.

In this chapter I will look in some depth at the theory behind oscillations and at simple harmonic motion in particular. I will also look at damping of vibrations, and the need for damping in practical applications such as car suspension systems.

Stationary, or standing, waves have special importance in music. I will look at the theory behind these waves and consider their application to such instruments as guitars and organ pipes.

SIMPLE HARMONIC MOTION

Most of us at some time have seen a grandfather clock with a pendulum. The reason for using a pendulum is that the time taken for each swing through a small angle is constant. So, as the pendulum swings back and forth, it controls very precisely the movement of the clock’s mechanism.

The pendulum is an example of an oscillator – it moves backwards and forwards in a regular (periodic) way. The period of the pendulum is the time it takes to go from one position in its swing through a complete oscillation back to its original position. The time taken for the pendulum to swing is constant, provided the angle of swing is small. Galileo noticed this as he watched a lamp swing on a chain in Pisa Cathedral. The number of such oscillations in a unit of time is called the frequency. The distance the bob has swung away from its central equilibrium position is called its displacement, and the maximum displacement is the amplitude of swing.

^{burro, CC BY-SA 3.0}

Another example of an oscillator is a mass vibrating up and down on the end of a spring. Here also, the mass moves up and down past a central position.

Displacement is movement in a particular direction and therefore is a vector. For the mass on the spring, displacement x (and also amplitude) is measured in metres. For the pendulum, displacement is measured as an angle, @, usually in radians.

The period T is measured in seconds. Frequency f is the number of vibrations in a second, and so we have the inverse relationship:

F =1/T

We can see that the unit of frequency is second^-1(i.e. s^-1). This unit of frequency is given the special name hertz (Hz). This means that:

1 Hz = 1 s^-1

Remember that a radian is the angle subtended at the centre of a circle (in this case the pivot of the pendulum) by an arc equal in length to the radius. (Here, the radius is the length of the pendulum.)

To find out more about oscillations, we can fix a pen to a pendulum and swing the pendulum over a moving strip of paper on, for example, a dynamics trolley moving at right angles to the swing of the pendulum. The pen plots a trace which represents the displacement of the pendulum with time. This is the sequence of events:

• At time t = 0 the pendulum is set swinging by letting it fall away from a position of maximum displacement. This displacement is the amplitude A of swing.
• The pendulum has zero displacement (it hangs vertically) at time t = T/4.
• At time t = T/2, the pendulum has maximum displacement on the side opposite its start side.
• The pendulum again has zero displacement at t = 3T/4 as it returns back through the vertical position.
• The pendulum takes time T to do a complete swing and return to its original position.

If you are familiar with a plot of cos θ against θ, then you will recognize this as the curve in the figure below. The movement of such an oscillating system is called simple harmonic motion because many musical instruments create vibrations like this. We say that the path of the motion varies sinusoidally – that is, like a sine (or cosine) curve.

^{User:Evil_saltine, Public Domain}

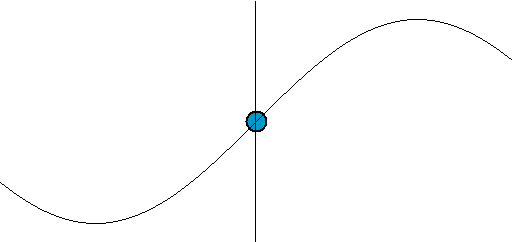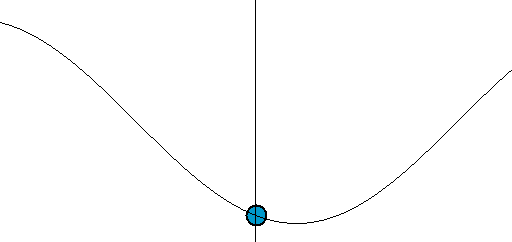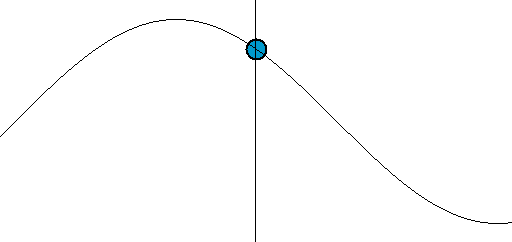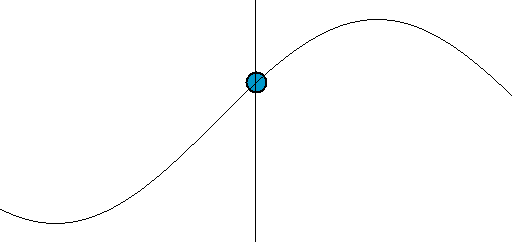
MAPPING SIMPLE HARMONIC MOTION ONTO A CIRCLE

It helps us to understand simple harmonic motion if we link it to movement in a circle. We can place a sphere near the edge of a rotating turntable and project a shadow of the sphere onto a screen. As the turntable rotates, the shadow of the sphere moves across the screen with a motion similar to that of the bob of a pendulum moving back and forth.

For another demonstration, we can use a vibrating dynamics trolley as is shown below. The trolley is attached to two fixed posts using two identical springs. At equilibrium, the trolley sits centrally between the posts with the springs pulling equally in opposite directions. When the trolley is pulled to one side, the two springs both act, with a force proportional to the displacement x, to return the trolley to the central equilibrium position. This restoring force F is given by:

F = -kx

Where k is the spring constant for the combination of the two springs. Note that when one spring is compressed and tending to lengthen, the other is stretched and tending to shorten. When the trolley returns to its central position, it has a velocity that makes it overshoot. It goes on to achieve maximum displacement on the other side.

We can trace the change of position of the trolley with time by connecting the trolley to a ticker-tape machine. We get a series of dots at equal time intervals as the trolley moves from maximum displacement on one side of the equilibrium position to maximum displacement on the other side.

We can see that the dots are not equally spaced along the strip of paper, and we can match them up with points which are equally spaced around a semicircle. It is as if a spot is moving with constant angular speed around the circle, just as the sphere was moving uniformly around with the turntable.

The spot would make one complete revolution, covering an angle of 2ω radians, in period T. Its angular speed ω is obtained from angle turned through, divided by time. That is:

Angular speed ω = 2π/T = 2πf

From the Fig, we see that the displacement of the oscillating trolley is given by:

x = A cos θ = A cos ωt

Where A is the maximum amplitude of the oscillation. This is an equation for simple harmonic motion (sometimes abbreviated to s.h.m.).

^{Svjo, CC BY-SA 3.0}

EXAMPLE

A trolley oscillates with amplitude 5.0 cm and period 2.5 s. What are its displacements relative to its equilibrium position 0.4 s and 1.0 s after being set off from a position of maximum amplitude?

To answer this question, we first need to find π in radians. (Your calculator needs to be in radian mode.)
We have seen that

ω = 2πf and f = 1/T

So: f = 1/25 = 0.4 Hz
And ω = 2π x 0.40 s-1

This gives us a displacement after 0.4 s of:

x = A cos ωt
= 5.0 cos(2π x 0.40 x 0.4)
= 5.0 cos(1.01)
= 2.7 cm

That is, the trolley is 2.7 cm from the equilibrium position, on the same side as it started.

After 1.0 s:

X = 5.0 cos(2π x 0.40 x 1.0)
= 5.0 cos(2.51)
= -4.0 cm

That is, the trolley is 4.0 cm from the equilibrium position, on the opposite side from where it started.

Till next time when I shall be discussing the displacement, velocity, and acceleration in simple harmonic motion and some other interesting topics on oscillations and waves, I remain the humble @emperorhassy.

Thank you for reading.

REFERENCES

https://en.wikipedia.org/wiki/Oscillation
http://www.odu.edu/~jdudek/Phys111N_materials/8_oscillations_waves.pdf
https://www.cpp.edu/~pbsiegel/supnotes/nts1322.pdf
https://www.khanacademy.org/science/physics/mechanical-waves-and-sound
https://www.britannica.com/science/simple-harmonic-motion
https://www.khanacademy.org/science/ap-physics-1/simple-harmonic-motion-ap/introduction-to-simple-harmonic-motion-ap/a/introduction-to-simple-harmonic-motion-review
https://en.wikipedia.org/wiki/Simple_harmonic_motion
https://www.ck12.org/c/physics/simple-harmonic-motion/lesson/Simple-Harmonic-Motion-PHYS/
http://canu.ucalgary.ca/map/classes/info/shm/spring/lesson.html
https://www.khanacademy.org/computing/computer-programming/programming-natural-simulations/programming-oscillations/a/oscillation-amplitude-and-period
https://cse.wwu.edu/physics/simple-harmonic-motion-shm-and-uniform-circular-motion-ucm-spring
https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_