Equilibrio líquido-vapor en sistemas binarios. Miscibilidad total
Cuando hablamos de los equilibrios entre fases, uno de los equilibrios que tiene suma importancia para la industria es el equilibrio liquido-vapor, ya que es la base para los procesos de separación como la destilación, un proceso ampliamente utilizado en la industria y en general clave para los diseños en ingeniería.
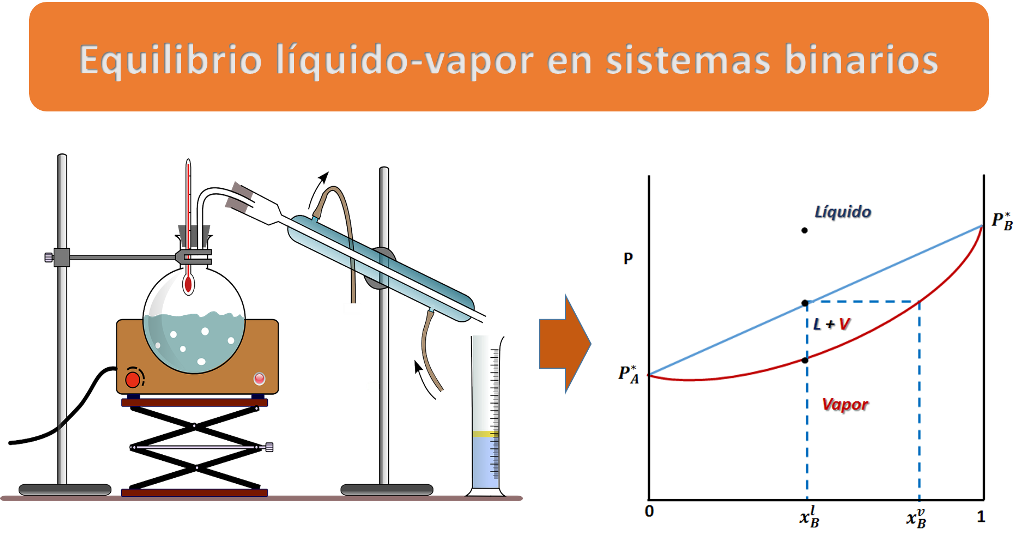
El equilibrio líquido-vapor es el fundamento de la destilación. Fuente: imagen elaborada en powerpoint, contiene imagen de dominio público:
Comprender las condiciones de equilibrio líquido-vapor es fundamental para entender la interacción y comportamiento de los componentes en una mezcla, y esto nos permite construir el diagrama de fases del sistema, lo cual es fundamental para realizar el análisis del sistema y realizar las respectivas operaciones de diseño y control de un proceso de destilación, en el cual se busca extraer los componentes puros.
Por lo general, los datos de equilibrio líquido-vapor para una mezcla se obtienen de forma experimental mediante el método de destilación simple o fraccionada, llevados a cabo bajo ciertas condiciones de temperatura y presión.
En este post abordáramos la descripción y análisis del equilibrio líquido-vapor de mezclas binarias, en la cual ambos componentes son miscibles entre sí y volátiles, por la importancia que tiene esta operación de separación de una mezcla de componentes líquidos para el laboratorio y la industria.

Arreglos típicos de equipos de destilación en el laboratorio y en la industria. Fuente: imagenes de dominio público.
Equilibrio líquido-vapor
Cuando nos referimos a un equilibrio líquido-vapor hacemos referencia a una condición aparentemente estática en las propiedades macroscópicas de un sistema donde se encuentran en contacto una fase líquida con su vapor, aunque realmente es una condición muy dinámica a nivel microscópico, en el cual las moléculas de la fase líquida están en constante movimiento hacia la fase vapor y viceversa, por lo que la concentración global del líquido y el vapor permanecen constante.
Sistemas binarios
En un anterior post describí las características del equilibrio de fases en sistemas compuesto por un componente, ahora veamos cómo se comporta el sistema cuando el sistema está compuesto de dos componentes, es decir, es un sistema binario.
Cuando C = 2 en la regla de las fases de Gibbs, la cual es L = C-F+2, tendremos que, en un sistema con dos componentes y una fase, que podría ser una por ejemplo una mezcla líquida de etanol y agua, entonces tendremos que L=3, es decir, son necesarias tres variables intensivas e independientes para describir el sistema; estas tres variables serian la presión (P), la temperatura (T) y la fracción molar (X) de uno de los dos componentes.
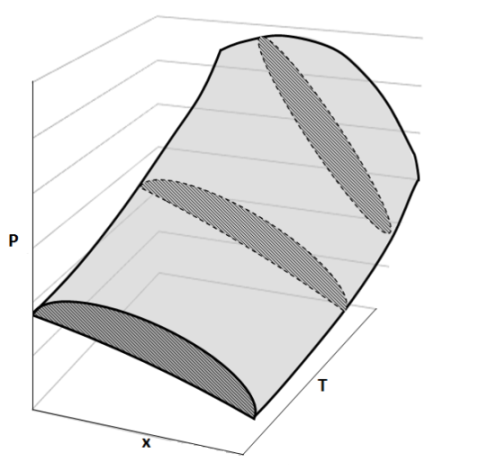
Representación de un diagrama tridimensional P,T,x para el equilibrio líquido-vapor. Fuente: imagen elaborada en Powerpoint.
Como vemos en la figura anterior, esta forma de representación puede resultar compleja, así que, por conveniencia, se suele mantener la presión o la temperatura constante y se representa gráficamente un diagrama bidimensional. Por lo que, si trazamos un plano horizontal que atraviese el grafico de forma perpendicular al eje P, las líneas sobre este plano representan un diagrama T,x a varias presiones. Del mismo modo, si trazamos un plano vertical perpendicular al eje T, las líneas sobre el plano representaran un diagrama P,x a varias temperaturas.
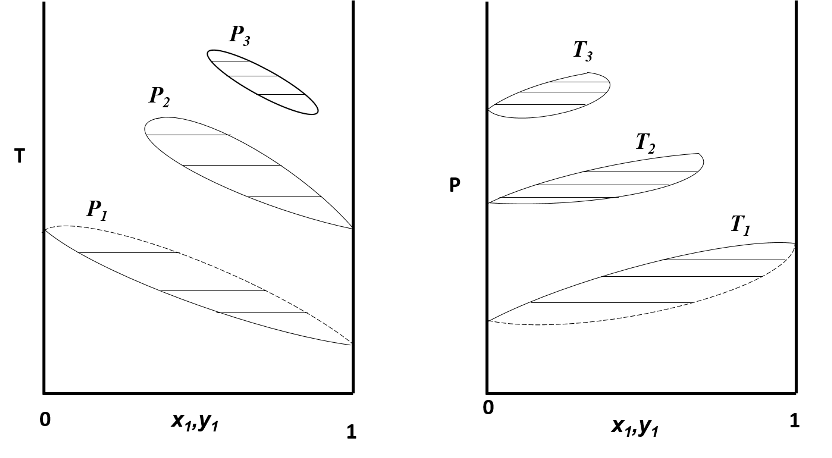
Diagrama Tx,y a tres presiones (izquierda) y diagrama Px,y a tres temperaturas. Fuente: imagen elaborada en Powerpoint.
Equilibrio líquido-vapor en disoluciones ideales a Temperatura constante
Si reducimos la presión aplicada sobre una mezcla de dos líquidos (A y B) que forman una disolución ideal, manteniendo la temperatura constante en un valor por encima del punto de congelación de ambos líquidos, la disolución comenzará a vaporizarse, obteniéndose un sistema bifásico compuesto por la disolución en equilibrio con su vapor. En este sistema, las fracciones molares de los dos componentes en la fase líquida suelen ser diferentes a las presentes en la fase vapor.
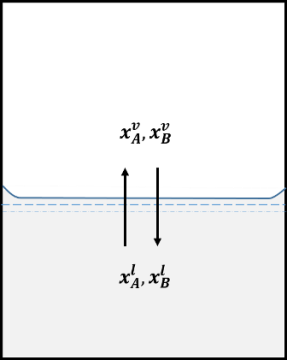
Fracciones molares en equilibrio a una temperatura T en una disolución ideal. Fuente: imagen elaborada en powerpoint.
Vamos a suponer que el sistema se encuentra en el interior de un cilindro cerrado por un pistón, algo así como en el interior de una jeringa, y que a su vez, se encuentra en un baño con control de temperatura.
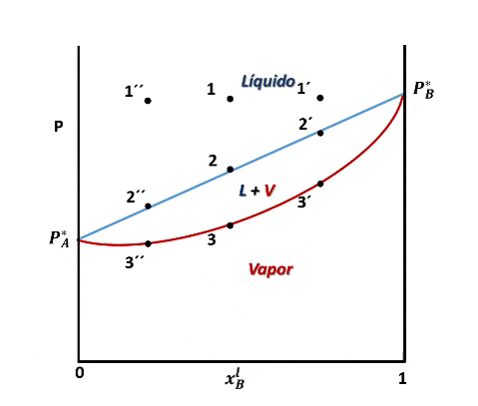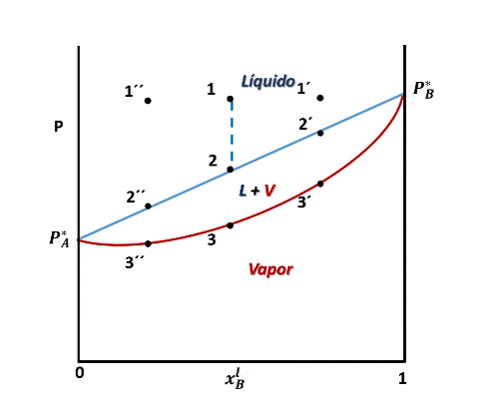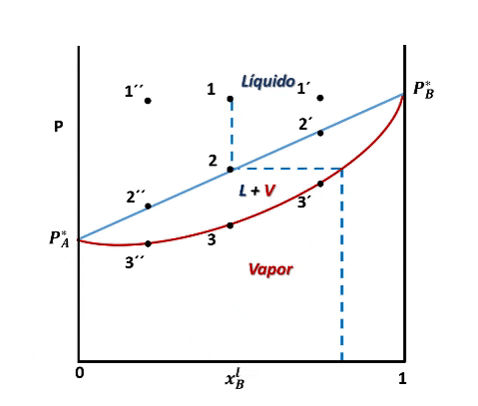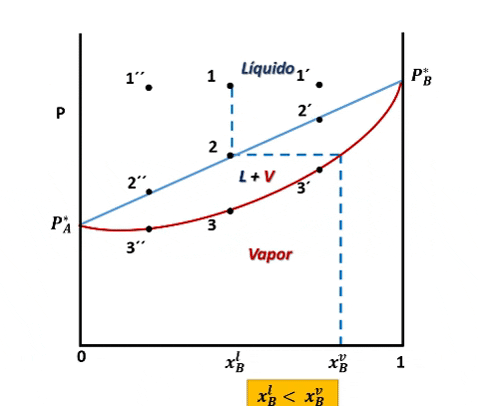
Entonces, para ver cómo se forma el diagrama de fases P vs xB supondremos que en la posición inicial del pistón la presión es lo suficientemente alta como para que el sistema se encuentre totalmente en fase líquida (punto 1 en la figura), luego, si se desplaza el pistón disminuyendo la presión por debajo del punto 1, llegará un instante en que se alcance un valor de P en el cual el líquido comienza a vaporizarse, punto 2, apareciendo la primera burbuja de vapor. Si la presión continua disminuyendo mayor será la cantidad de vapor formado, hasta que finalmente se vaporice la última gota de líquido, punto 3, y por debajo de este punto 3 solo existirá vapor.
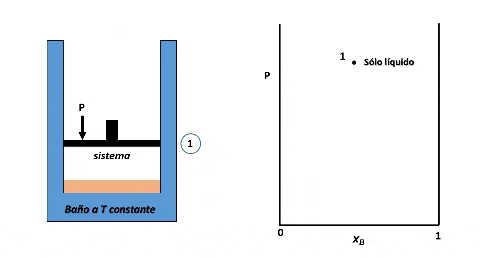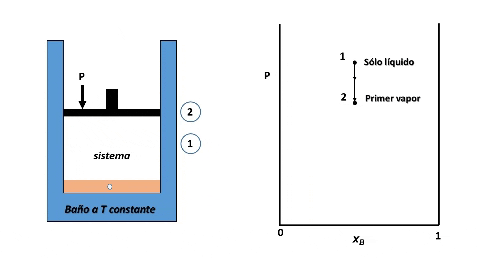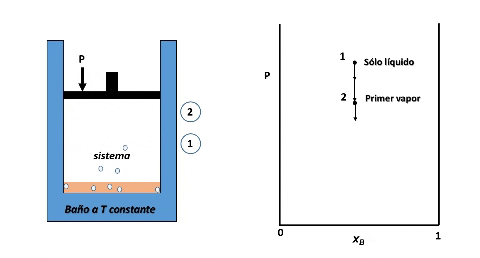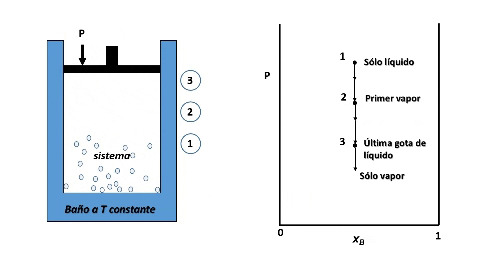
Formación de fases en el sistema. Fuente: @emiliomoron
Para cualquier valor de P que se ubique entre las presiones del punto 2 y 3, el sistema estará compuesto por la fase líquida y la fase vapor coexistiendo en equilibrio. Y si repetimos este procedimiento varias veces, tomando cada vez una fracción molar xB diferente, cubriendo el rango de composiciones de 0 a 1, representando el valor de P en el cual el líquido comienza y termina de vaporizar, obtendremos el diagrama de fases del sistema.
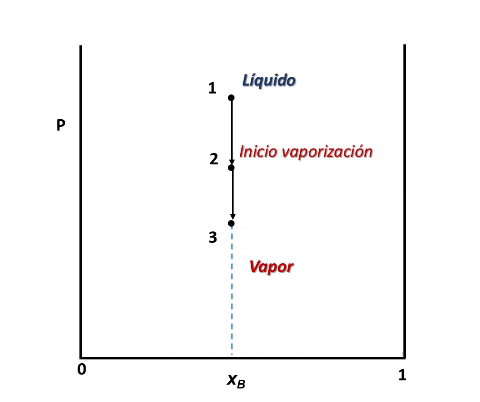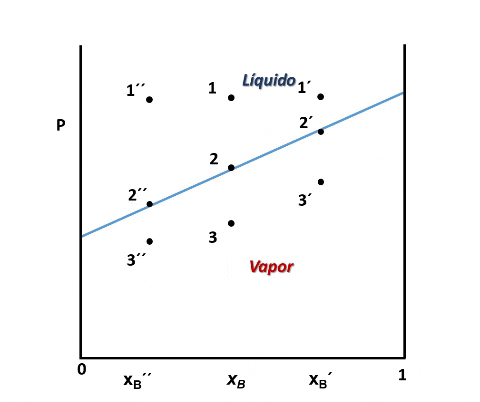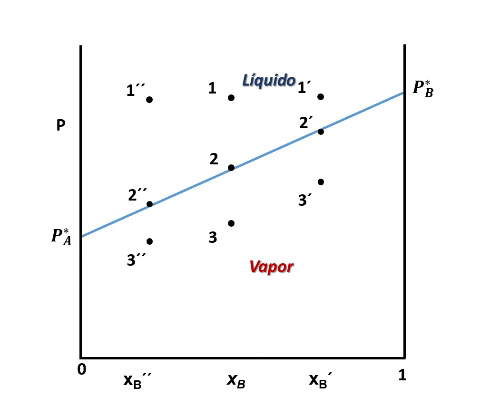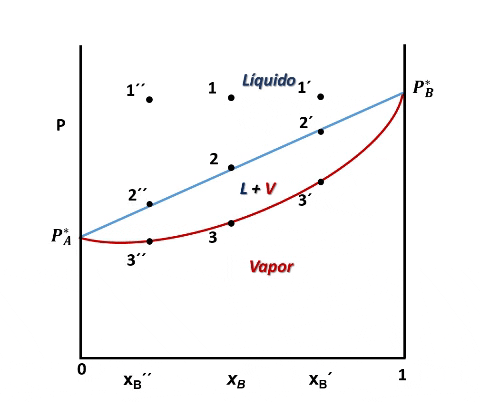
La vaporización de muestras con diferentes composiciones permiten representar el diagrama de fases. Fuente: @emiliomoron.
Entonces, en el diagrama de fases P vs xB a T constante presenta tres regiones, para cualquier punto por encima de la línea 1,1´,1´´ el sistema es monofásico y se encuentra en fase líquida, en cualquier punto por debajo de la línea 2,2´, 2´´ solo existirá vapor, y en un punto entre ambas curvas tendremos un equilibrio entre ambas fases.
En el punto 2 la fracción molar xBl resulta ser prácticamente igual a la composición global xB, ya que la fracción vaporizada es una cantidad infinitesimal del líquido, no siendo suficiente para cambiar su composición. Por otro lado, la fracción molar del primer vapor formado viene dada por la ley de Raoult, con la cual se puede relacionar las fracciones molares del vapor con las fracciones molares del líquido de la siguiente forma:
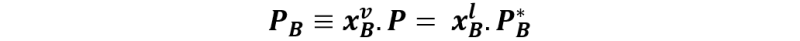
Donde PB es la presión parcial del líquido B, P es la presión de vapor sobre la solución, y PB* es la presión de vapor del líquido B puro a la temperatura del sistema. De esta forma, la fracción molar del vapor se determina como:
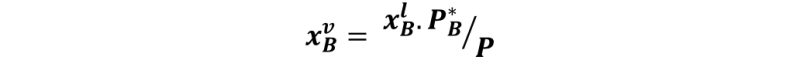
¿Cómo podríamos determinar las curvas de equilibrio?
Cuando se unen lo puntos 2, 2´ y 2´´obtenemos una línea en cuyos puntos el líquido está comenzando a vaporizarse, la presión de vapor es P = PA + PB, o lo que es lo mismo:
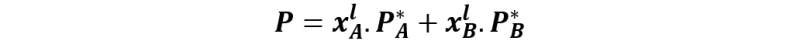
Y como xAl + xBl = 1, podemos escribir la expresión como:
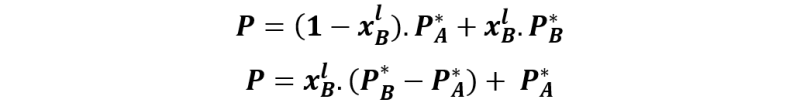
La ecuación anterior corresponde a la línea que empieza en el valor PA* para una xBl = 0 y finaliza en el valor P*B cuando xBl = 1.
Ahora bien, a lo largo de la curva que une los puntos 3, 3´y 3´´ la última gota de líquido se está vaporizando, por lo que la composición viene dada por la fracción molar del líquido B en el vapor, xBv. Entonces, para graficar esta curva de P frente a xBv basta con transformar xBl que aparece en la ecuación anterior en una función de xBv, eso lo podemos hacer sustituyendo la relación xBl = xBv.P/ P*B dada por la ley de Raoult en la expresión de la curva y despejando P:
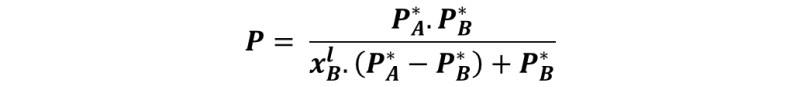
De esta forma podemos observar que todo líquido que se somete a una vaporización formará un vapor cuya composición guarda relación con la fracción molar del líquido, y si el líquido B es el componente más volátil, lo que quiere decir que PB* PA*, entonces el vapor formado por encima de la disolución se va a ir enriqueciendo en el componente más volátil, siendo esto el principio de la separación de componentes por destilación.
El vapor formado se enriquece con el componente más volatil. Fuente: @emiliomoron.
Como vemos, comprender cómo ocurre la formación del equilibrio líquido-vapor nos ayuda ainterpretar adecuadamente un diagrama de fases de este tipo de equilibrio, especialmente uno tan útil en la industria y el laboratorio.
Bueno amigos, espero que esta introducción al equilibrio líquido-vapor nos ayude a interpretar mejor el diagrama de fases para un sistema binario a temperatura constante que forma disoluciones ideales, en otro post analizaremos este diagrama cuando el sistema es sometido a una vaporización a presión constante.
¡Hasta la próxima!
Referencias
Maron & Prutton (2006). Fundamentos de fisicoquímicada. Editorial Limusa.
Levine, I. (2004). Fisicoquímica. Editorial McGraw Hill.
Y amigo lector, si desean consultar más artículos de interés científico y de excelente calidad, visiten la etiqueta #STEM-espanol, este es un proyecto adscrito a la comunidad académica y científica #STEMSocial en Hive, una comunidad que promueve contenido científico en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas.
Congratulations @emiliomoron! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 100000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Ciao a tutti, desideravo un nuovo paio di scarpe da trekking per le mie escursioni in Appennino, ma i modelli performanti avevano prezzi elevati. Una guida escursionistica mi ha consigliato https://spin-granny.it , lodando le loro offerte stagionali per gli italiani. I miei inizi sono stati difficili, una lunga serie di sconfitte ha minato il mio morale. Stavo per chiudere l'account, quando ho alzato la posta su un gioco a tema montagna e ho centrato un bonus con una vincita sostanziosa. Il ricavato ha finanziato le scarpe e uno zaino tecnico. Per gli escursionisti in Italia, può essere un vero colpo di fortuna.