Deducción de la regla de las fases de Gibbs
Como sabemos existen diferentes tipos de equilibrio, pero uno de los más útiles es el equilibrio material, las transiciones de fases son los procesos físicos más utilizados en las operaciones industriales, como la destilación, la cristalización o la separación líquido-líquido, por eso representar adecuadamente los equilibrios de fases es un paso muy importante cuando se estudian este tipo de operaciones.
Y aunque cada tipo de equilibrio es tratado de forma particular, hay una ecuación que nos permite tratarlos con un enfoque unificado, este principio de la química se conoce como la regla de las fases de Gibbs, con esta ecuación el número de grados de libertad de un sistema termodinámico queda definido cuando se establecen algunas condiciones para el equilibrio.

Regla de las fases de Gibbs. Fuente: @emiliomoron.
Regla de las fases de Gibbs
Antes de continuar debemos aclarar los conceptos de fase, componentes y grados de libertad. Recordemos que una fase es la porción de nuestro sistema bajo estudio que tiene las mismas propiedades físicas y químicas, los componentes son las especies químicas que se encuentran presentes y los grados de libertad corresponden al número mínimo de variables que necesitamos para que quede completamente definido, es decir, cuantas variables podemos modificar sin alterar la estructura y composición del sistema. Podemos consultar más información en mi anterior post sobre las definiciones de fase y componentes.
Ahora bien, J. Willard Gibbs en 1876 estableció que hay una relación fija entre las fases, el número de componentes y los grados de libertad para un sistema en equilibrio, a esta relación se le denominó como regla de la fases, y aunque es un principio muy general es una ecuación muy útil para el estudio de los equilibrios heterogéneos.
Podemos deducirla de la siguiente forma, consideremos que tenemos cierto sistema en equilibrio, compuesto de C componentes y F fases, el problema es establecer el número de variables que definen el sistema. Así que lo que vamos a hacer es determinar el mínimo número de variables independientes que necesitamos para describir el sistema. Por ejemplo, la temperatura y la presión son variables intensivas necesarias para describir cualquier estado de equilibrio, así que necesitamos especificar una o ambas variables (T y P).
Por otro lado necesitamos definir la composición de cada fase, para ello debemos definir la concentración de los componentes que se encuentran presentes, pero aquí no necesitamos saber la concentración de todos, ya que no todas estas variables son independientes entre sí. Partiendo de la suposición de que las especies químicas están presentes en todas las fases y que no ocurre una reacción entre ellas, si tenemos un sistema donde hay solo dos componentes, basta con conocer la concentración de uno de ellos, la del otro queda definida por la relación X1 + X2 = 1, así que basta especificar las concentraciones de C-1 componentes, ya que la del otro queda definida por diferencia.

Para describir la composición de una solución basta con identificar C-1 concentraciones. Fuente: @emiliomoron.
Y como hay F fases vamos a necesitar entonces F(C-1) variables. Y junto con la presión y la temperatura necesitamos entonces F(C-1)+2 variables para describir el sistema.
Entonces, si hay n variables también habrá n ecuaciones para determinar el valor de cada una, así que debemos saber cuál es el número de ecuaciones que relacionan a estas variables, y para ello utilizaremos la termodinámica. Esto nos dice que el equilibrio entre dos fases es posible solo si la energía libre molal parcial de cada constituyente es igual a la del mismo constituyente en la otra fase.
Así que, además de las ecuaciones de composición también tenemos las condiciones de equilibrio, que para el equilibrio material se cumple que el potencial químico de un mismo componente ha de ser igual en cada fase.

La igualdad entre potenciales ofrecen relaciones de dependencias entre variables. Fuente: @emiliomoron.
Como hay F fases, entonces habrá F-1 condiciones de equilibro para cada constituyente, y como existen C especies químicas entonces tendremos un total de C(F-1) relaciones de equilibrio que se pueden utilizar para eliminar la misma cantidad de variables intensivas, ya que los potenciales químicos son una función de la presión, la temperatura y la composición .
Entonces, el número de variables intensivas independientes de definen los grados de libertad (L) de un sistema es:
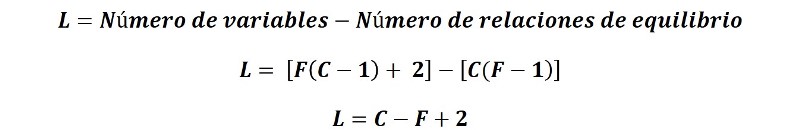
La ecuación anterior es la conocida regla de las fases. Donde L, los grados de libertad, dan el número de variables que deben especificarse para que el estado del sistema quede caracterizado sin ambigüedad.
Veamos estos ejemplos.
1.- Si queremos representar el estado termodinámico de un sistema compuesto por agua y su vapor en equilibrio, procedemos de la siguiente forma.
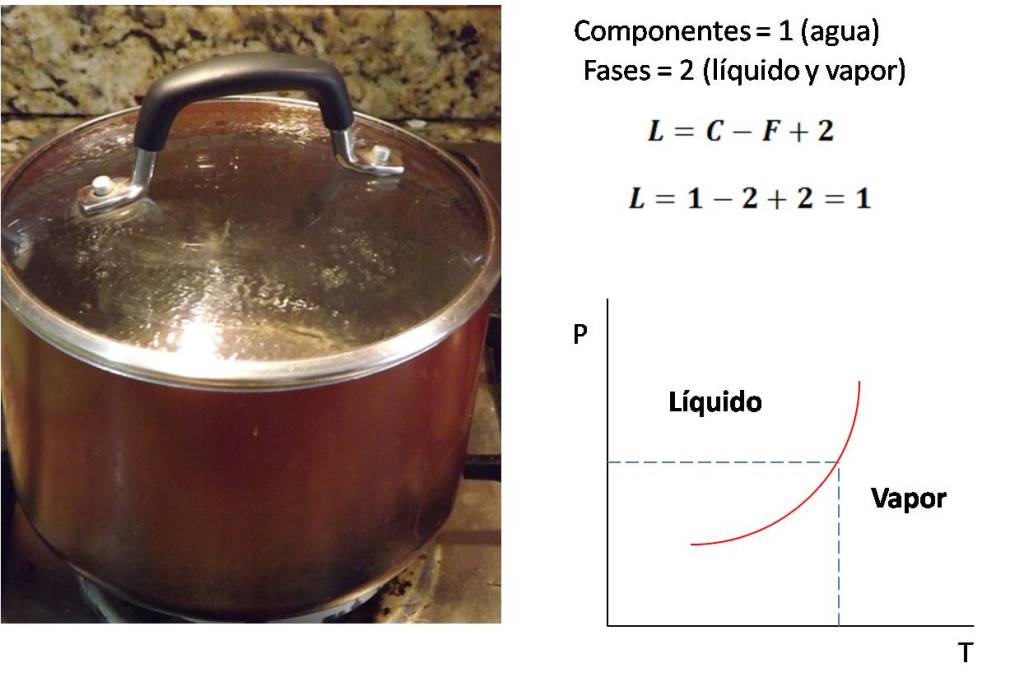
Grados de libertad para el sistema agua en equilibrio con su vapor. Fuente: @emiliomoron.
Esto quiere decir que necesitamos solo una variable para definir sin ambigüedades el sistema, y ya que hay un solo componente, esta variable podría ser T o P. Por ejemplo, es bien sabido que el agua hierve a 100 °C a 1 atm de presión, así que podemos notar que a otra presión el agua hervirá a otra temperatura, de modo que si tenemos un sistema compuesto por agua en equilibrio con su vapor y al medir la temperatura el sistema está a 100 °C, automáticamente podemos suponer que la presión del sistema es 1 atm. Así que con definir la T de este equilibrio, la P que establecida por dependencia.
2.- ¿Cuántos grados de libertad se necesitan para un sistema compuesto por sacarosa sólida en equilibrio su disolución?

Grados de libertad para una solución saturada de sacarosa. Fuente: @emiliomoron.
En este caso necesitamos de dos variables para describir el sistema, lo cual es lógico, ya que la cantidad de sacarosa para obtener una disolución saturada dependerá de la solubilidad en dicho solvente, y el solvente solo admite una cantidad específica de soluto a determinada temperatura y presión.
Como vemos, cuando determinamos el valor de L podemos describir completamente un sistema en equilibrio, ya que el resto de las propiedades intensivas de cada fase se pueden establecer. Así por ejemplo, cuando se especifica la temperatura y la presión de la solución de sacarosa, podemos determinar propiedades como la densidad, la fracción molar y la capacidad calorífica, entre otras, ya que estas son dependientes de las otras dos y la concentración.
Bueno amigos espero que la información les haya gustado y sea de utilidad para comprender el fundamento fisicoquímico del equilibrio entre fases. ¡Hasta la próxima!
Referencias
Maron & Prutton (2006). Fundamentos de fisicoquímicada. Editorial Limusa.
Y amigo lector, si desean consultar más artículos de interés científico y de excelente calidad, visiten la etiqueta #STEM-espanol, este es un proyecto adscrito a la comunidad académica y científica #STEMSocial en Hive, una comunidad que promueve contenido científico en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Muchas gracias por el apoyo amigos!