Physics - Classical Mechanics - Exercises around Newtonian Gravity (part 2)

[Image1]
Introduction
Hey it's a me again @drifter1!
In this article we will continue with Physics, and more specifically the branch of "Classical Mechanics".
Today's article is part two of Exercises on Newtonian Gravity.
Part 1 can be found here.
So, without further ado, let's dive straight into it!
Recap of Useful Formulas
The following formulas will be very useful for solving Problems around Gravity.Universal Law of Gravitation

where:
- d is the distance of the COMs of the two masses m1 and m2
- G is the Gravitation Constant which equals 6.674 × 10-11 N
Weight or Force of Gravity
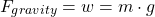
Gravitational Acceleration
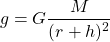
where:
- r can be thought of as the median radius of a planet
- h as the height of an object in respect to the surface of the planet
Gravitational Potential Energy

or
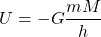
ΔU = U2 - U1 is thus negative when the height decreases (h1 > h2).
Gravitational Potential

Two-Dimensional Problem's Field Acceleration
Let's start by calculating the Gravitational Acceleration g of the two-dimensional gravity problem that we solved during Part 1.
The total force aplied on mass mA = 4 Kg was calculated to be ΣF = 2.059 x 10-11.
Thus, the Gravitational acceleration g at the point where mA is in the field of the three other masses is:

Gravitational Field on the Axis of a Ring (based on Ref1)
Let's consider the following gravitational field along the axis of a uniform ring:
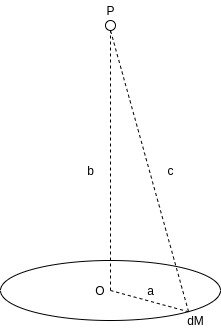
[Custom Figure using draw.io]
The ring has a mass of M and a radius of a, and the points P are taken at a distance b along the axis of the ring. At the center of the ring the Gravitational field of course has a strengh of zero.
Let's find the maximum strength of the Gravitational Field along the axis of the ring in respect to the distance from the center O.
Solution
In order to calculate the field of a ring, the ring has to be split into small masses dM, whose fields can then be summed up together.
The distance towards each of those small masses is equal to c, which can be easily calculated using Pythagoras's Theorem:
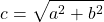
The total gravitational field strengh dg of each of those masses dM is:
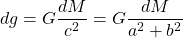
Because each field dg points towards another direction a split of each vector into two components is necessary.
Doing that its easy to notice that there is another mass dM' that cancels out one of the components completely, which is something that happens for all masses dM:
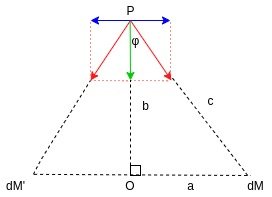
[Custom Figure using draw.io]
Thus, only the component parallel to the axis of the ring will contribute towards the field strength.
Using the trigonometric function of cosinus, this component is defined as:
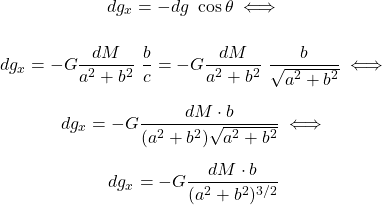
Summing up the contributions of all those small masses dM, the total gravitational field g along the axis of the ring is calculated to be:
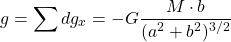
The maximum value is reached at the point(s) where the derivative of g, g', is zero.
The derivative is equal to:
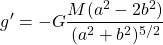
The nominator is zero when:

Therefore, the maximum value is at a distance of b = a / √2, which gives us a field strength of:

The plot of the gravity field strength g in respect to the distance b, supposing that G = M = a = 1, looks as following:
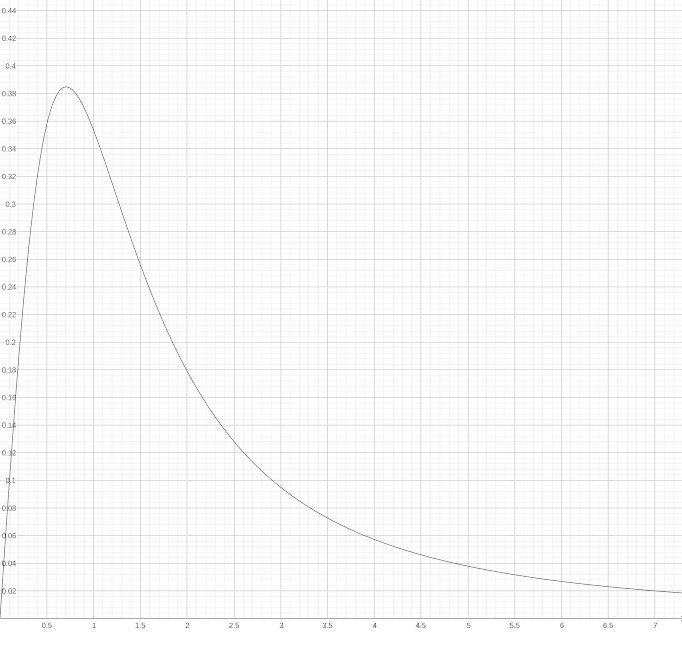
[Custom Figure using GeoGebra]
Speed of a Rollercoaster (Inversed Example 2 of Reference 2)
Consider a rollercoaster starts going down from an unknown height h and reaches a final speed of v = 25 m / s.
Find the value of h if friction is negligible and g = 9.8 m/s2.
Solution
The initial velocity of the rollercoaster is zero (Kinitial = 0) and thus the rollercoaster initially has only gravitational potential energy.
The final potential energy is zero (Ufinal = 0), and thus, from Energy conservation, the initial potential energy equals the final kinetic energy, or mathematically:
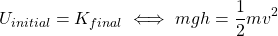
The mass is cancelled out and the rest is known and thus the initial height h is:
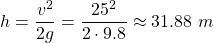
RESOURCES:
References
- https://phys.libretexts.org/Bookshelves/Astronomy__Cosmology/Book%3A_Celestial_Mechanics_(Tatum)/05%3A_Gravitational_Field_and_Potential/5.04%3A_The_Gravitational_Fields_of_Various_Bodies/5.4.02%3A_Field_on_the_Axis_of_a_Ring
- https://courses.lumenlearning.com/physics/chapter/7-3-gravitational-potential-energy/
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
- Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Internal Energy and Work -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Angular Motion
- Angular motion basics -> Angular position, velocity and acceleration
- Rotation with constant angular acceleration -> Constant angular acceleration, Example
- Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
- Parallel Axis Theorem -> Parallel axis theorem with example
- Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
- Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
- Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
- Angular Momentum -> Angular Momentum and its conservation
- Explaining the Physics behind Mechanical Gyroscopes -> What they are, History, How they work (Precession, Mathematical Analysis) Difference to Accelerometers
- Exercises around Angular motion -> Angular motion examples
Equilibrium and Elasticity
- Rigid Body Equilibrium -> Equilibrium Conditions of Rigid Bodies, Center of Gravity, Solving Equilibrium Problems
- Force Couple System -> Force Couple System, Example
- Tensile Stress and Strain -> Tensile Stress, Tensile Strain, Young's Modulus, Poisson's Ratio
- Volumetric Stress and Strain -> Volumetric Stress, Volumetric Strain, Bulk's Modulus of Elasticity, Compressibility
- Cross-Sectional Stress and Strain -> Shear Stress, Shear Strain, Shear Modulus
- Elasticity and Plasticity of Common Materials -> Elasticity, Plasticity, Stress-Strain Diagram, Fracture, Common Materials
- Rigid Body Equilibrium Exercises -> Center of Gravity Calculation, Equilibrium Problems
- Exercises on Elasticity and Plasticity -> Young Modulus, Bulk Modulus and Shear Modulus Examples
Gravity
- Newton's Law of Gravitation -> Newton's Law of Gravity, Gravitational Constant G
- Weight: The Force of Gravity -> Weight, Gravitational Acceleration, Gravity on Earth and Planets of the Solar System
- Gravitational Fields -> Gravitational Field Mathematics and Visualization
- Gravitational Potential Energy -> Gravitational Potential Energy, Potential and Escape Velocity
- Exercises around Newtonian Gravity (part 1) -> Examples on the Universal Law of Gravitation
Final words | Next up
And this is actually it for today's post!
Next time we will get into a Physics explanation of the circular motion of Satellites...
See ya!

Congratulations @drifter1! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPThanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.