Physics - Classical Mechanics - Black Holes and Schwarzschild Radius

[Image1 - First Image of a Black Hole - Messier 87]
Introduction
Hey it's a me again @drifter1!
In this article we will continue with Physics, and more specifically the branch of "Classical Mechanics".
Today's topic are Black Holes and the so called Schwarzschild Radius.
So, without further ado, let's get straight into it!
Black Holes
First of all, Black holes aren't actually holes. Black holes are stars that have collapsed gravitationally, so much that not even light can escape. Stars achieve a certain balance between the crushing force of gravity and the push of the incredibly hot gases. This balance exists, because there is fuel to burn in the fusion process within the star. When the fuel runs out then gravity collapses the star, and the more massive the star, the more intense the collapse.
Small Stars become White Dwarfs
Stars about the size of the Sun collapse into something called a white dwarf. After their fuel runs out, gravity produces enough pressure for electrons and nuclei to be packed tightly together. The result is an object about the size of the Earth.
Large Stars become Neutron Stars
Stars in the range of six to eight times the size of the Sun undergo a catastrophic explosion known as a supernova. The force of gravity jams the electrons together into the nuclei creating a neutron star, with a small diameter of some Kms. The neutron star stage is the final combination and the forces between the neutrons prevent further collapse.
Massive Stars turn into Black Holes
Stars that are ten or more times larger then the sun collapse even the neutron core, thus forming a black hole. The repulsion that prevented the neutron star to collapse cannot withstand the gravity force of about two to three solar masses. Gravity near a black hole is so strong that not even light can escape it. And matter or radiation inside the sphere of influence of the black hole, known as the event horizon, falls inward and cannot escape. A black hole with ten times the mass of the sun, has an event horizon of about 30 Km.
Types of Black Holes
Massive stars of about 10-100 times the size of the Sun turn into galactic black holes. In the center of galaxies roam supermassive black holes - *insert Muse song* - that can range up to billions of solar masses in size.
How to See Them
From their definition black holes are invisible. Its possible to identify stellar black holes by observing light that disappears in a binary star system, where one of the stars is a black hole. Black holes also emit X-rays and larger ones even form a swirling gas disk around the event horizon.
Schwarzschild Radius
The Schwarzschild Radius (or gravitational radius), is the radius below which the gravitational attraction between the particles of a body forces it to undergo an irreversible gravitational collapse. Its the radius below which massive stars turn into black holes. The radius was investigated in the early 20th Century by German astronomer and physist Karl Schwarzschild.
Mathematically, this radius can be calculated as follows:
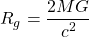
where:
- G : the gravitational constant (6.674 × 10-11 Nm2/kg2)
- M : the mass of the object (in Kg)
- c : the speed of light (~3 × 108 m/s)
One Solar mass
For the sun, with a mass of about 1.989 × 1030 Kg, to become a black hole, it must be compressed into a radius of:

Three Solar Masses
An object of three solar masses needs to be compressed to at least:
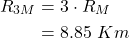
Earth
What needs to be the radius of the Earth, mass of 6 × 1024 Kg, for it to turn into a black hole?
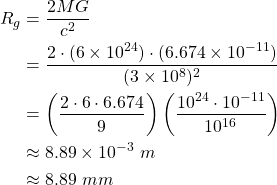
The Earth needs to be compressed into a 8.89 mm radius, which is extremely small. Only some bits larger then the thickness of a strand of hair, which is in the range of 0.04 to 0.1mm!
Human
Lastly, Can a human also become a black hole?
The answer is of course Yes, but what is the Schwarzschild Radius for a let's say 60 Kg Human being?

Alright that's infinitesimal small. An atom is in the scale of picometers (pm) 10 -12 m, meaning that a human has to become smaller then an atom, which is basically impossible.
RESOURCES:
References
- https://www.physicscentral.com/explore/action/blackholes.cfm
- https://astronomy.swin.edu.au/cosmos/S/Schwarzschild+Radius
- https://www.britannica.com/science/Schwarzschild-radius
- http://hyperphysics.phy-astr.gsu.edu/hbase/Astro/blkhol.html
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
- Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Internal Energy and Work -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Angular Motion
- Angular motion basics -> Angular position, velocity and acceleration
- Rotation with constant angular acceleration -> Constant angular acceleration, Example
- Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
- Parallel Axis Theorem -> Parallel axis theorem with example
- Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
- Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
- Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
- Angular Momentum -> Angular Momentum and its conservation
- Explaining the Physics behind Mechanical Gyroscopes -> What they are, History, How they work (Precession, Mathematical Analysis) Difference to Accelerometers
- Exercises around Angular motion -> Angular motion examples
Equilibrium and Elasticity
- Rigid Body Equilibrium -> Equilibrium Conditions of Rigid Bodies, Center of Gravity, Solving Equilibrium Problems
- Force Couple System -> Force Couple System, Example
- Tensile Stress and Strain -> Tensile Stress, Tensile Strain, Young's Modulus, Poisson's Ratio
- Volumetric Stress and Strain -> Volumetric Stress, Volumetric Strain, Bulk's Modulus of Elasticity, Compressibility
- Cross-Sectional Stress and Strain -> Shear Stress, Shear Strain, Shear Modulus
- Elasticity and Plasticity of Common Materials -> Elasticity, Plasticity, Stress-Strain Diagram, Fracture, Common Materials
- Rigid Body Equilibrium Exercises -> Center of Gravity Calculation, Equilibrium Problems
- Exercises on Elasticity and Plasticity -> Young Modulus, Bulk Modulus and Shear Modulus Examples
Gravity
- Newton's Law of Gravitation -> Newton's Law of Gravity, Gravitational Constant G
- Weight: The Force of Gravity -> Weight, Gravitational Acceleration, Gravity on Earth and Planets of the Solar System
- Gravitational Fields -> Gravitational Field Mathematics and Visualization
- Gravitational Potential Energy -> Gravitational Potential Energy, Potential and Escape Velocity
- Exercises around Newtonian Gravity (part 1) -> Examples on the Universal Law of Gravitation
- Exercises around Newtonian Gravity (part2) -> Examples on Gravitational Fields and Potential Energy
- Explaining the Physics behind Satellite Motion -> The Circular Motion of Satellites
- Kepler's Laws of Planetary Motion -> Kepler's Story, Elliptical Orbits, Kepler's Laws
- Spherical Mass Distributions -> Spherical Mass Distribution, Gravity Outside and Within a Spherical Shell, Simple Examples
- Earth's Rotation and its Effect on Gravity -> Gravity on Earth, Apparent Weight
Final words | Next up
And this is actually it for today's post!
Next time we will get into a new chapter of Classical Mechanics: "Periodic Motion".
See ya!

@tipu curate 2
Upvoted 👌 (Mana: 90/150) Liquid rewards.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Congratulations @drifter1! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz: