Mathematics - Signals And Systems - Continuous-Time Periodic Signals & Fourier Series
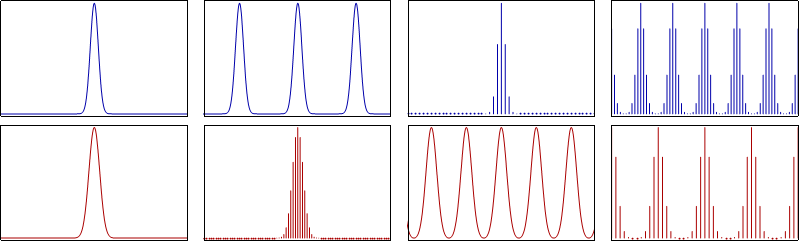
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover Continuous-Time Periodic Signals & Fourier Series.
I highly suggest reading the previous article about Discrete-Time, as the representation is quite similar, in some sense.
So, without further ado, let's get straight into it!
Input Decomposition
Let's start simple, by basically refreshing our knowledge around linear systems, and why they are so useful...
First of all, due to the properties of linear systems, and mainly due to the principle of superposition, its possible to decompose any signal into a set of basic signals. The expected outcome of this procedure is a linear combination of basic signals for which the response can be easily computed.
Consider a signal x(t) in continuous-time.
For linear systems, this signal can be decomposed to as a linear combination of φk 's in the following way:
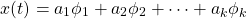
In the end, what matters is that the response of the system will be some combination of easy to compute ψk 's:
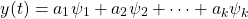
Those ψk 's are the result of convolution for each of the basic φk 's.
In continuous-time, the convolution integral can be represented as:
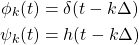
Basic Signals and the Concept of Fourier Analysis
As we already mentioned in some previous article, the main concept of Fourier analysis is using complex exponentials as the set of basic signals.
Thus, the basic signals will be of the form:
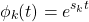
Substituting sk with jωk, its easier to see the "complex" part:
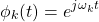
When sk is complex the transform is also known as a Laplace transform.
The system response for such a signal is:
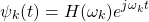
For periodic signals the result will be represented by a Fourier Series, whilst for aperiodic signals (which will be covered next time) the outcome is a Fourier Transform.
Fourier Series - Sum of Complex Exponentials
A Fourier Series is basically a weighted sum of complex exponentials, which are harmonically related.
Its known that a signal is periodic only when the following relation is true:
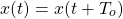
where To is the period.
The period To can be substituted using the following equation:
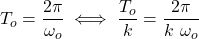
which allows us to replace the ωk's by the product k ωo :
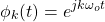
In this notion, a periodic signal x(t) can be decompsed into a sum of complex exponentials as such:
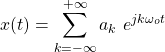
Fourier Synthesis
The coefficients, ak, can be calculated using:

for which I will skip the proof.
Trigonometric form
In the article about complex exponentials, it was shown how Euler's Relation can be used to get a trigonometric form.
In this case, the trigonometric form looks as follows:
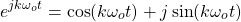
which results in the following complete decomposition of x(t) :

where ak = Bk + jCk and the harmonic relation between the complex exponentials is also taken into consideration.
The coefficients, ak, can be still calculated using the same equation as before, with ao having the special property of being the average value of x(t) during a period.
This is basically an alternative way of representing the complex exponentials that form the Fourier Series, where each exponential is a linear combination of sines and cosines, or sinusoids in general, of different phase angles.
Signal Approximation
Incorporating only 2N + 1 terms of the Fourier Series, its possible to end up with an approximation of x(t) in the form of signal xN(t).
This signal is represented by the sum:
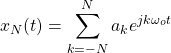
Doing that we introduced an error eN(t), which can be calculated by:
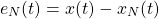
As N increases, the error eN(t) is generally decreasing, as we end up with a better approximation of the signal x(t).
RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io
Previous articles of the series
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
Final words | Next up
And this is actually it for today's post!
Next time we will cover Aperiodic Signal in Continuous-Time, which are represented using something known as the Fourier Transform.
See Ya!

Keep on drifting!
This is a good reference for those who are currently studying signals and systems or digital signal processing. By the way, your reference (Oppenheim) is a good notes for the subject matter. I used that one when I had my signals class.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.