Mathematics - All About Trigonometry (Part 4)

over 3 years ago

Introduction

Hey it's a me again @drifter1!

Today we continue with the small series about Trigonometry. I suggest reading the first, second and third part before getting into this one. Today we will cover Trigonometric Identies and Equations!

So, without further ado, let's get straight into it!

Trigonometric Identities

After covering basic Trigonometry, and solving right and general (non-right) triangles, it's time to get even more advanced! First off, let's cover Trigonometric Identities, which are equations that contain only Trigonometric Functions. Trigonometric Identities are useful for simplifing expressions, so that they contain only sine and cosine ratios.

Quotient Identity

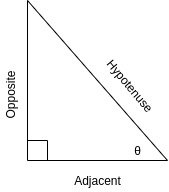
[Custom Figure using draw.io]

For a right triangle with an angle θ, we defined that the main trigonometric functions are:

Dividing Sine by Cosine we get:

And so the first identity is:

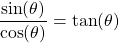
Something similar is also true for the cosecant (csc), secant (sec) and cotangent (cot) functions:

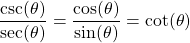
Square Identity

From Pythagoras's Theorem we can also derive an useful identity, that we already covered in a previous article. There we used the Unit circle and the values of the axes, but the same identiy can also be proven using a different approach.

In a right-triangle with Hypotenuse c, dividing a² + b² = c² by c² gives us:

Similarly, it's also possible to define the following Identities:

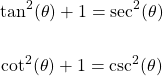
Opposite Angle Idenitites

In a previous article we covered how the values of the trigonometric functions change as we move from Quadrant to Quadrant. The values follow the pattern: "A-S-T-C" or "All-Sine-Tangent-Cosine", giving the following identities as a result:

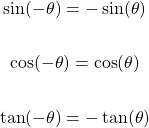
Double Angle Identities

If we double the angle θ that is "fed into" each trigonometric function the result can also be written in respect to θ as follows:

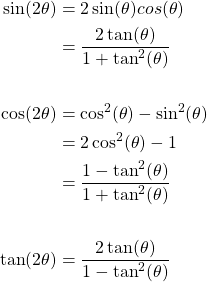
Half Angle Identities

Similarly, it's also possible to write half the angle θ in respect to trigonometric functions containinig θ:

Angle Sum and Difference Identities

The result of an trigonometric function that takes in a sum of two angles A and B can be written using trigonometric functions that contain only A and B respectively:

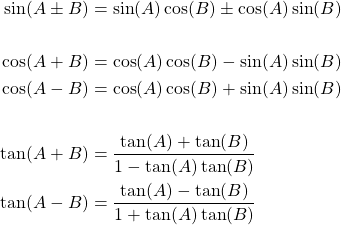
In the case of the sine function, that same sign has to be used in both sides!

Product to Sum Identities

A product between trigonometric functions of possibly different angles, x and y, can be turned into a sum:

Sum to Product Identities

A sum between trigonometric functions of possible different angles, x and y, can be turned into a product:

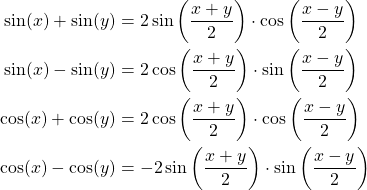
Laws of General Triangles

Of course the Law of Sines and Law of Cosines can also be used as Idenitites. And there is also something called the Law of Tangents, that we didn't cover before.

Mathematically:

Solving Trigonometric Equations

Equal Sines, Cosines and Tangents

Two angles θ and φ, which are both less than 360°, give us the same result for the trigonometric functions. How are those two angles related?

Sine

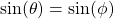
Sine has the same value in Quadrants A-B (positive) and C-D (negative), meaning that θ = 180° - φ or φ = 180° - θ.

Cosine

Cosine has the same value in Quadrants A-D (positive) and B-C (negative), meaning that θ = 360° - φ or φ = 360° - θ

Tangent

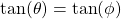
Tangent has the same value in Quadrants A-C (positive) and B-D (negative), meaning that θ = φ - 180° or φ = θ - 180°

Solutions of a simple Trigonometric Equation (Example of Reference 5)

Consider the following equation:

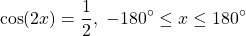
What is the value of x?

Solution

The Cosinus function gives 1 / 2 in the case of 60° degrees. The same is also true for 360° - 60° = 300°, because Quadrant A and D have the same value. Using the idenitity of the opposite angle (cos(-θ) = cos(θ)), we also get -60° and -300°.

Thus:

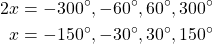
Using Trigonometric Identities this way, any equation is solveable or simplifiable!

General Solutions of a Trigonometric Equation (Example 17 of Reference 7)

Consider the following equation:

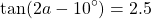
Let's find the general solution for a.

Solution

For an angle x = 2a - 10°, the tangent tan(x) = 2.5 and so one solution is:

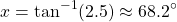
Solutions in the first quadrant:

Solutions in the third quadrant:

RESOURCES:

References

Images

https://commons.wikimedia.org/wiki/File:Academ_Base_of_trigonometry.svg

Mathematical equations used in this article, where made using quicklatex.

Final words | Next up

And this is actually it for today's post and this small series about Trigonometry!

Also, currently my ideas for "All About" articles include:

Geometry
Polynomial Arithmetic
Exponentials and Logarithms
Rational Expressions

Basically High-School Math Refreshers for Students in Universities or maybe even Middle-Age people that have problems helping their kids out in Math at school!

See ya!

Keep on drifting!