Solving Absolute Value Equations
Hi there. In this math post, I cover the topic of solving absolute value equations. Note that I do not feature applications here.
Topics
- Taking Absolute Values
- Absolute Value As A Piecewise Function
- Solving Basic Absolute Value Equations
- A Difficult Case
Taking Absolute Values
The absolute value of a number is the distance from the number to zero. Another way would be How far is the number in absolute value away from 0?. Taking the absolute value of 3 gives 3 as three is 3 units away from zero. The absolute value of negative 3 is also 3 as the number -3 is 3 units away from zero.
Here are some more examples:
|-10| = 10|5| = 5|77| = 77
Absolute Value As A Piecewise Function
This absolute value can be generalized into a function. This function is actually a piecewise function whose output depends on the input value. The variable x is commonly used as the input or independent variable. The f(x) notation would be used for the output for dependent variable.
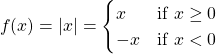
Transformations can be applied to the above function above to obtain absolute value functions such as |x + 7|, |2x - 5| and |10x - y|. Absolute value functions can be more complicated if they mix with quadratic functions, rational functions and other types of math functions.
Example
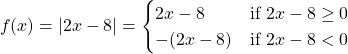
The above absolute value function is represented as a piecewise function. There is a problem though. The inequalities after the two ifs are not isolated for x. These inequalities have to be written such that x is isolated.
Solving the inequality 2x - 8 ≥ 0 leads to x ≥ 4 and the other one would lead to x < 4.

Solving Basic Absolute Value Equations
Solving absolute value equations can be tricky and annoying. Be aware of different cases when it comes to solving these.
Example One
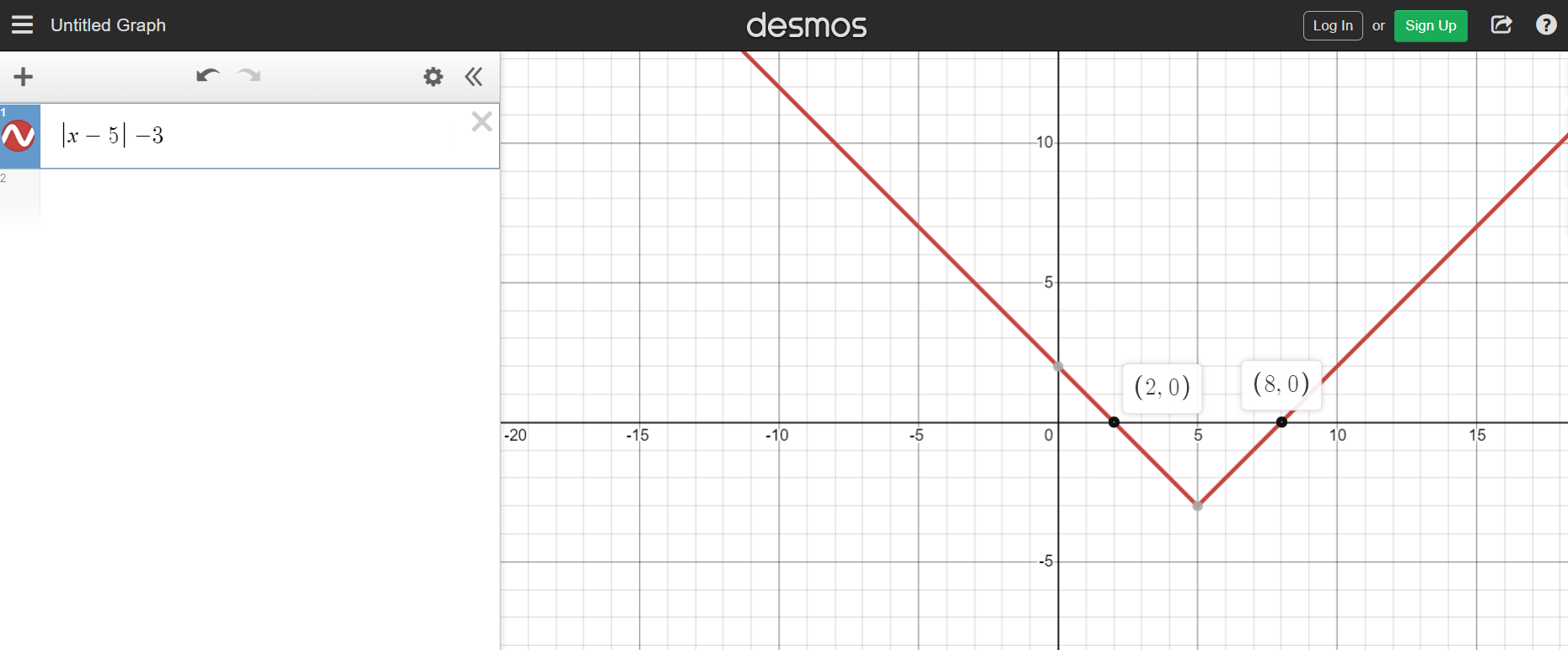
Solve for x in |x - 5| = 3.
The absolute value of a positive number is positive and the absolute value of a negative number is positive. There are two cases to consider when it comes to solving.
The first case is x - 5 = 3. This is where the stuff inside the absolute value bars is equal to 3. With the second case, there is the negative case. That is -(x - 5) = 3.
For the first case the answer is 8 from x - 5 = 3. With -(x - 5) = 3, there is -x + 5 = 3 which leads to the second solution of 2.
The Desmos screenshot below shows the graph of |x - 5| - 3 which is rearranged from |x - 5| = 3.
Example Two
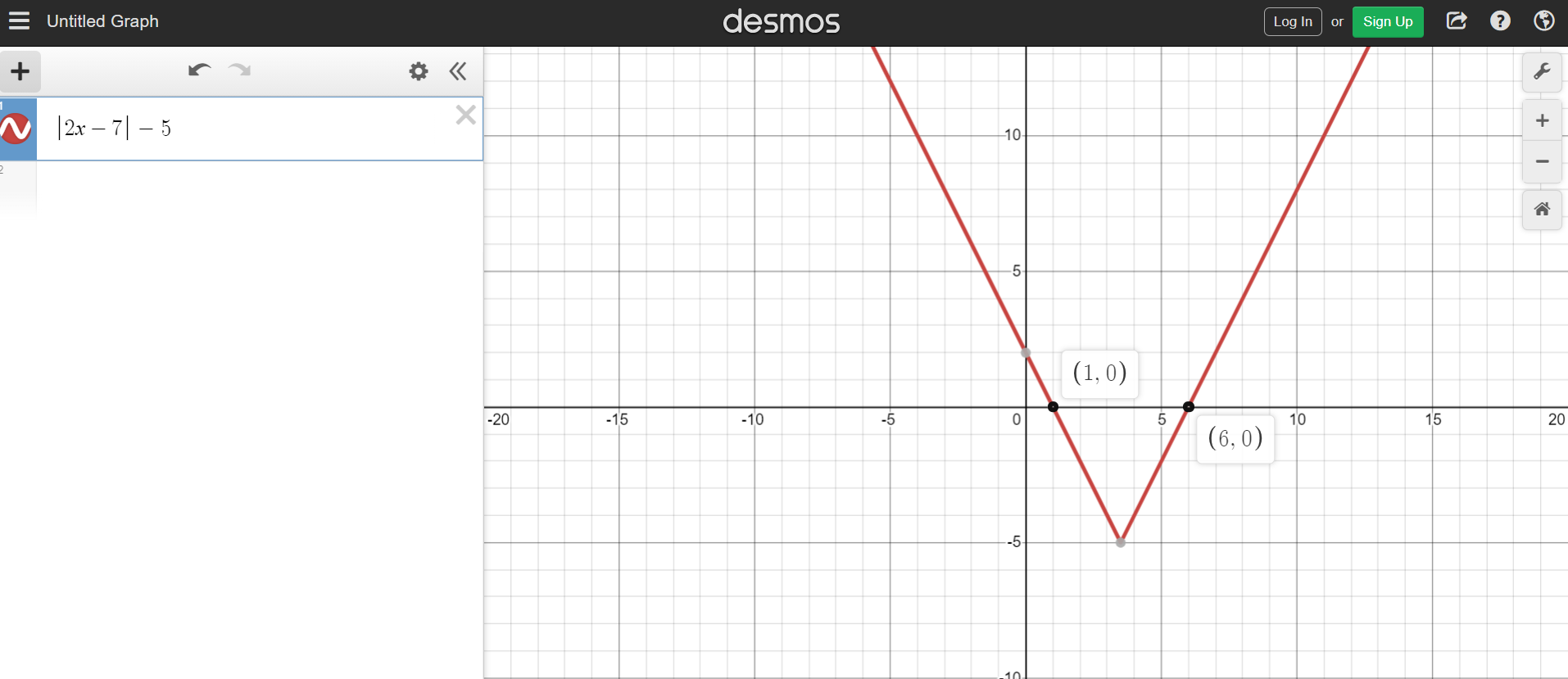
What is the value for x that satisfies |2x - 7| = 5?
Consider two cases. These are (2x - 7) = 5 and -(2x - 7) = 5.
From (2x - 7) = 5 solving for x leads into x = 6. With the other equation -(2x - 7) = 5 solving for x leads into x = 1.
Example Three - Simple Rational Function
Solve for x in |1/x| = 2.
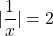
There are two cases when it comes to this case. Let's go through the first case.

Taking the reciprocal of both sides yields:
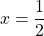
The second case would involve solving this equation:
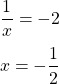
The two solutions here are half and negative half.
Example Four - Quadratic Function
Solve for x for 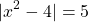 .
.
For this case, consider the two cases. The first case is:
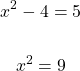
The solutions for x here are -3 and +3.
In the second case we have:
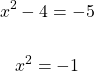
Taking the square root of both sides would result in a square root of negative one on the right side. There would be no real valued solutions in the second case. The valid values for x are ± 3 (plus or minus 3).
A Difficult Case
The examples so far had an absolute value function on one side of the equation. What if there absolute values on both sides? Here is one example where there is a linear function in absolute values on each side. A much tougher case would be having quadratic functions in absolute values on both sides.
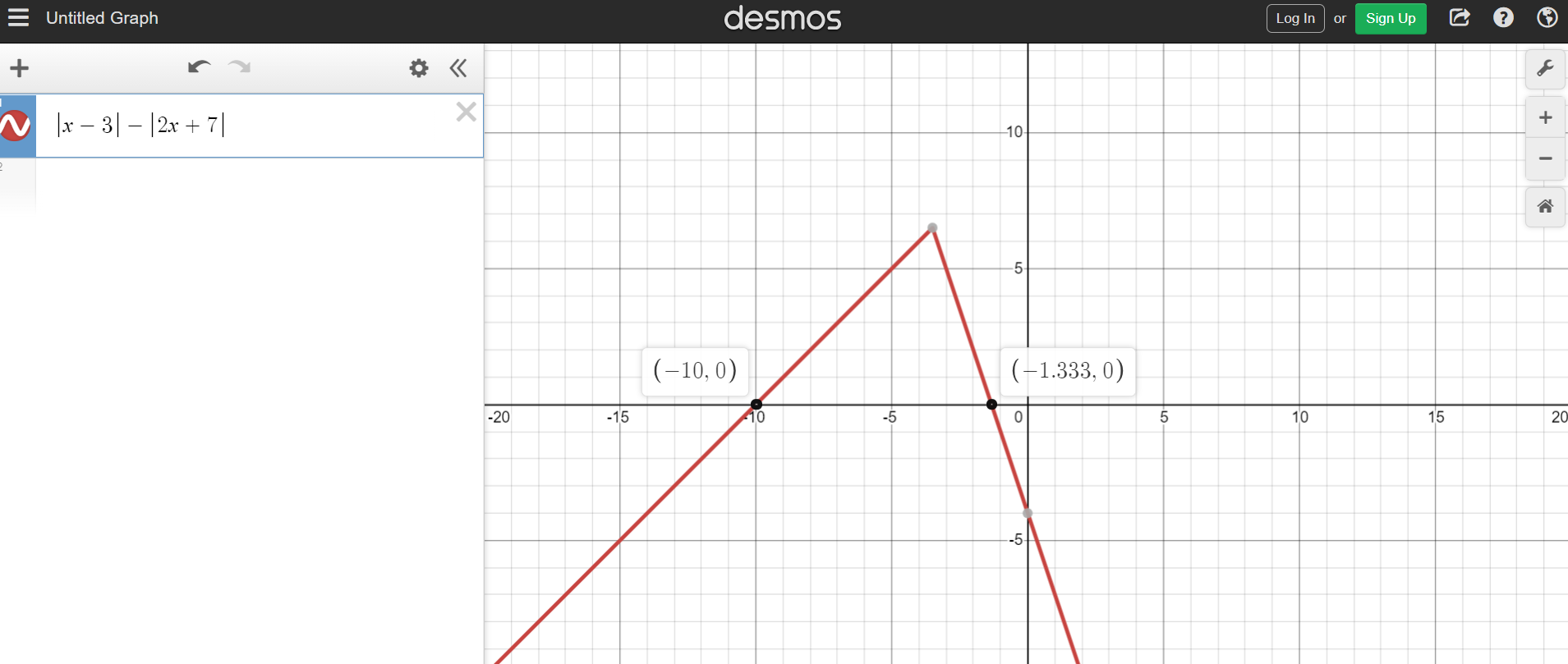
Solve for x in |x - 3| = |2x + 7|.
With this question, four cases are considered. These are:
- Both sides positive
- Left Side negative, right side positive
- Left Side positive, right side negative
- Both sides negative
What I mean by negative is that a negative sign is distributed to the entire linear function.
Case One - Both Sides Positive
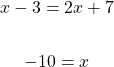
Case Two - Left Side Positive, Right Side Negative
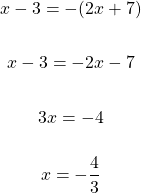
Case Three - Left Side Negative, Right Side Positive

Case Four - Both Sides Negative
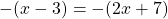
With both sides negative, this is pretty much the same as the case where both sides are positive. The negatives cancel each other out. I will still show the algebra below for this case.

The two answers for x that satisfy |x - 3| = |2x + 7| are -4/3 and -10. Desmos screenshot below.