Hi there. In this math post I cover the topic of golden ratio and its relation with the Fibonacci sequence of numbers.
Reference: https://mathsbyagirl.wordpress.com/2016/11/21/fibonacci-sequence-with-differential-equations/
I use LaTeX and Quicklatex.com for rendering the math text.
The Fibonacci Sequence Of Numbers
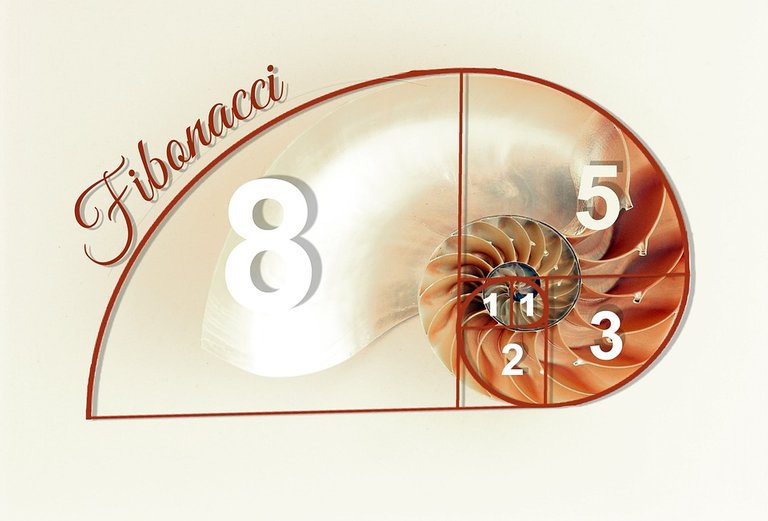
The Fibonacci sequence of numbers is a well known sequence of numbers. It starts with 0 and 1 as the first two numbers. The third number is the sum of 0 and 1 which is 1. The fourth number is the sum of the third number which is 1 and the second number which is 1. Obtaining the next number in the Fibonacci sequence involves taking the sum of the previous two numbers.
In math notation we would have:
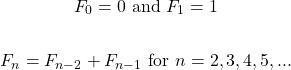
This is a recursive relation as obtaining the n-th Fibonacci number depends on the previous Fibonacci numbers.
Example
What is the seventh Fibonacci number in this sequence?
The seventh Fibonacci number is the sum of the sixth Fibonacci number and the fifth Fibonacci number.
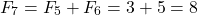
Eight is the seventh Fibonacci number.
Obtaining The Golden Ratio
So far we have the recursive relation for obtaining the n-th Fibonacci number.
With index shifting, the above can be rewritten such that there is no minus sign.
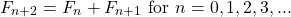
Let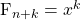 
. The Fibonacci relation from above is now into:
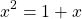
Setting the quadratic equal to zero yields:
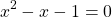
The quadratic equation is not factorable. Solving this quadratic requires the quadratic formula. For this case a = 1, b = -1 and c = -1.
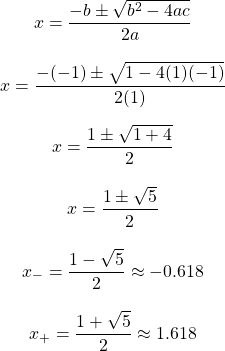
The answer of interest is the plus answer of the approximate value of 1.618. This represents the ratio of a Fibonacci number divided by the previous Fibonacci number.
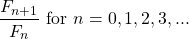
There is a lot more information on the golden ratio not covered in this post. I wanted to cover the derivation of the golden ratio with the use of Fibonacci numbers and the quadratic formula.
