Ejercicio # 5 de la sección 2.6 del libro de cálculo de Larson. Vol 1
Saludos amigos de la plataforma hive.
En esta oportunidad me puse a chequear el libro de cálculo de Larson volumen I, y encontré en los ejercicios propuestos de la sección 2.6 una serie de ejercicios propuestos en los cuales se indica una función determinada, de modo que la variación con las que se mueven dichos en x con respecto al tiempo es de 2 centímetros por segundo y se nos pide calcular dy/dt, es decir la variación de dicho punto de y con respecto al tiempo.
Dicha sección de ejercicios propuestos que se encuentran en la página 154 de dicho libro nos muestra los ejercicios del 5 al 8. Para el ejemplo que quiero explicar en el presente post voy a elegir el ejercicio # 5:
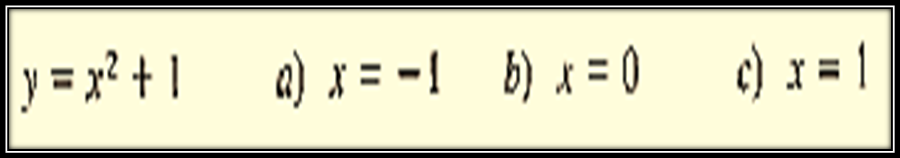
La función que vamos a analizar es una función parabólica y la vamos a evaluar para:
a.) x= -1
b.) x = 0
c.) x = 1
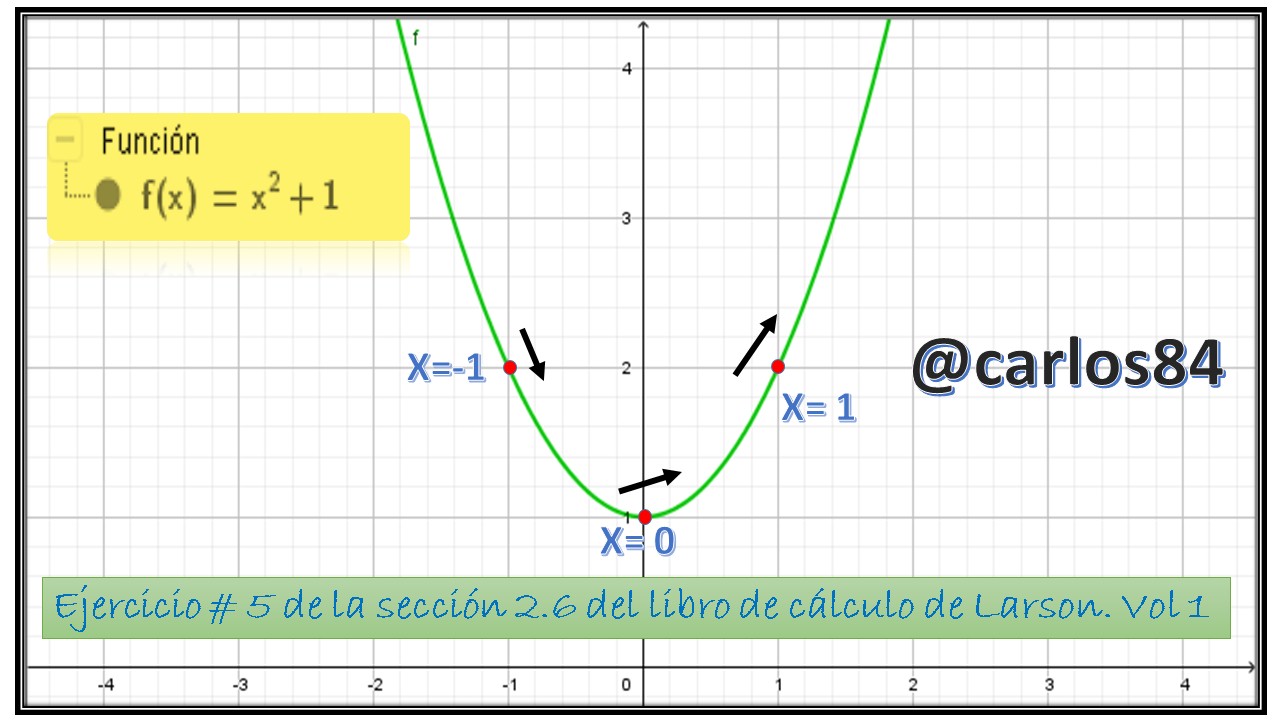
Ahora bien me gustaría presentarles como de costumbre el gráfico de la parábola empleando el software geogebra 5.0:
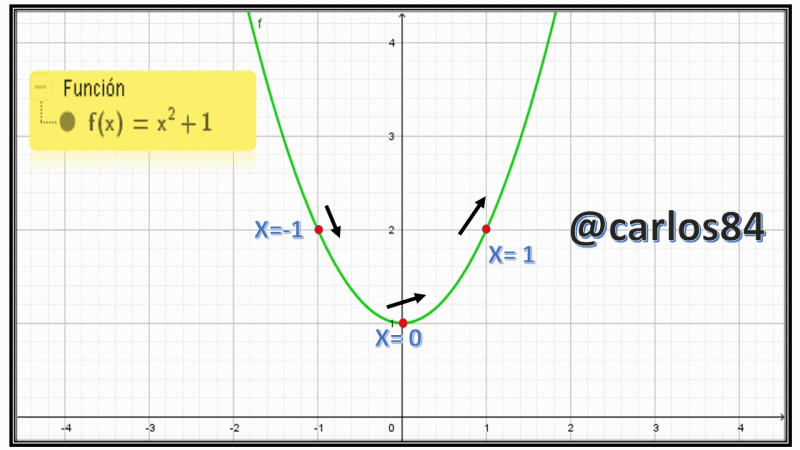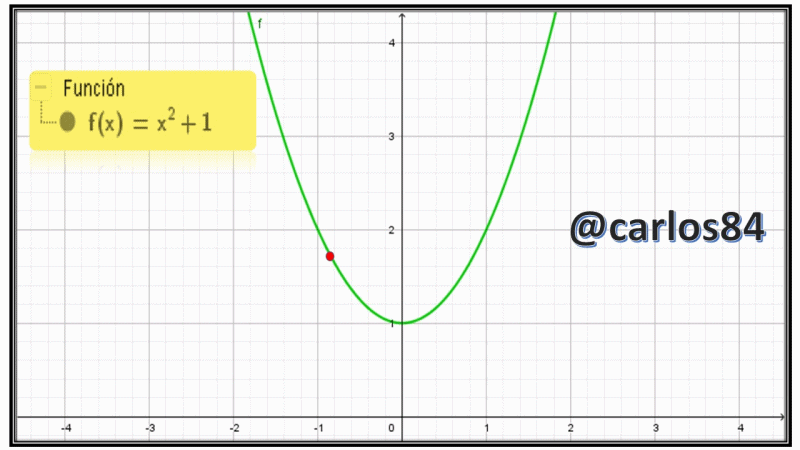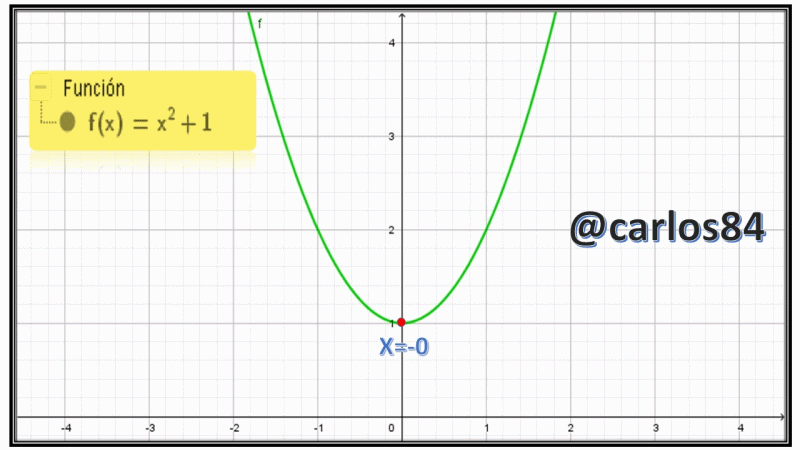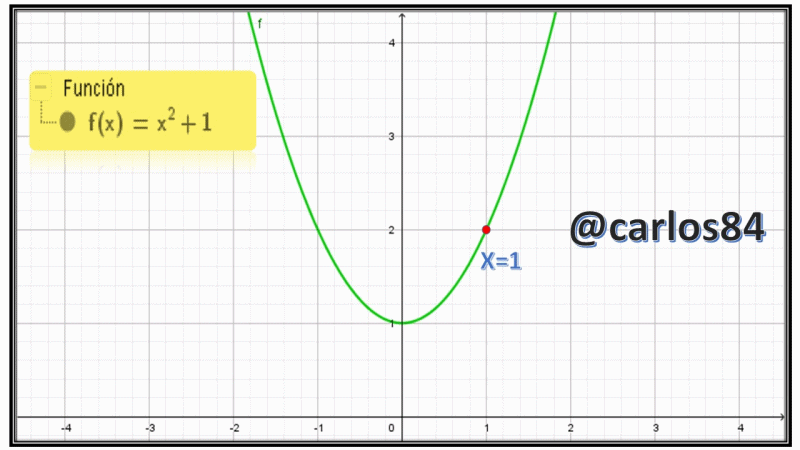
Como podemos observar en la imagen mostrada el punto rojo se desplaza con cierta velocidad, en el libro de Larson en la sección 2.6 del ejercicio # 5 se nos hace referencia que el punto viaja a una velocidad de 2cm/s sobre la parábola, ahora bien lo que vamos a encontrar es el dy/dt en x=-1, x= 0 y x= 1.
El desarrollo y explicación del ejercicio me gustaría que lo observaron en el siguiente vídeo de mi autoría:
Ver en Youtube
Referencia consultada y recomendad
Cálculo (completo) Vol 1 y 2 9na Edición Ron Larson & Bruce H. Edwards
Muy práctica la información, @carlos84. Me hace recordar la universidad.
Hola mi estimado amigo @eniolw.
Hoy repasando y viendo algunos ejercicios propuestos del Libro de Larson, ví este ejercicio propuesto en la sección 2.6 y me propuse a resolverlo y mostrar su resolución en este post, y que se que puede servir para muchos alumnos que están cursando cálculo en forma digital y a la distancia en la universidad.
Gracias por comentar amigo. Saludos
Su post ha sido valorado por @ramonycajal
Gracias por el apoyo a @ramonycajal y a @cervantes. Saludos