Effect of thixotropy in the drilling fluid

In this article referred to the thixotropic analysis of drilling fluid I will discuss two aspects that are of great relevance in well drilling, one is the effect of thixotropy in drilling fluids, whose analysis should be conclusive to know the impact of thixotropy in the drilling fluid, and the second aspect to be discussed is the description of pseudoplastic fluids as a fundamental part in the rheological study of drilling fluid.
Introduction
One of the problems commonly encountered in the drilling of oil wells is that while drilling there may be the eventuality of having to stop the circulation of drilling mud, when this happens and the well remains static it is necessary that the rock cuttings that were obtained during drilling are suspended, and thus do not remain above the drill bit, thus causing a sticking of pipe drill.
To keep the rock cuttings in suspension while there is no circulation (mud pumps off), it is necessary that the drilling mud has the ability to form a gelatinous structure, the mud acquires this gelatinous property the longer it is at rest, another factor that influences to reach the gel property is that certain additives are incorporated into the drilling mud such as bentonite (type of clay).
It should be noted that this ability of the fluid to create this gel property to keep the cuttings in suspension is studied through thixotropy.
This gelling capacity must maintain a balance as one of the most important properties in the drilling fluid, that is, when incorporating the relevant additives to incorporate this gelling property to the drilling fluid, it must be done taking into account that it is important to maintain the gelling capacity of the drilling fluid in the optimal operating values, it is necessary that the gel capacity is not so high as to create pistoning pressures at the bottom of the hole in which fractures can be induced to the formation.
Nor can this gel capacity be so low, as it would then not be possible to keep the riprap in suspension when the mud circulation in the hole is stopped.
It is important to mention that most drilling muds used to drill a hole have this gel capacity (thixotropy). However, a well prepared mud under a good thixotropic ratio must have the capacity to break this gel layer and return to its initial condition once the mud circulation can be restored.
Based on the above, we could say that drilling fluid thixotropy is a science that studies the ability of fluids to create a gel property when the well stops circulating (pumps off, static well), and at the same time recover its initial conditions once the drilling mud is circulated.
The counterpart of thixotropic fluids are pseudoplastic fluids, pseudoplastic fluids do not show a change in viscosity as time passes, which is why in this post, I will show a complete description of the two types of fluids and the marked differences between the two conditions, i.e. thixotropic and pseudoplastic fluids.
As we have seen in this brief introduction, thixotropy is the ability to control the gelation values so that you can operate in the drilling and construction of an oil well without any inconvenience, let's see what other factors are involved in the thixotropy of the drilling fluid (drilling mud).
Effect of thixotropy on drilling fluid

If we manage to measure the gel strength of a drilling fluid immediately after it has been agitated, after some time has passed since it was at rest and we measure it again, the values obtained will increase at a decreasing rate up to the point of reaching a maximum value.
This described behavior is known as the phenomenon of thixotropy.
What this means is that if we measure the thixotropy of the drilling mud in static conditions, its viscosity value must be such that it can keep the cuttings in suspension, but when the mud pumps are turned on and it is put into circulation, it must allow, through the effort that the mud pumps put on it, to break that gelation without generating higher pressures at the bottom of the well that may cause problems such as formation fracture pressures, or otherwise that there is too much demand from the mud pumps to be able to break that gelation.
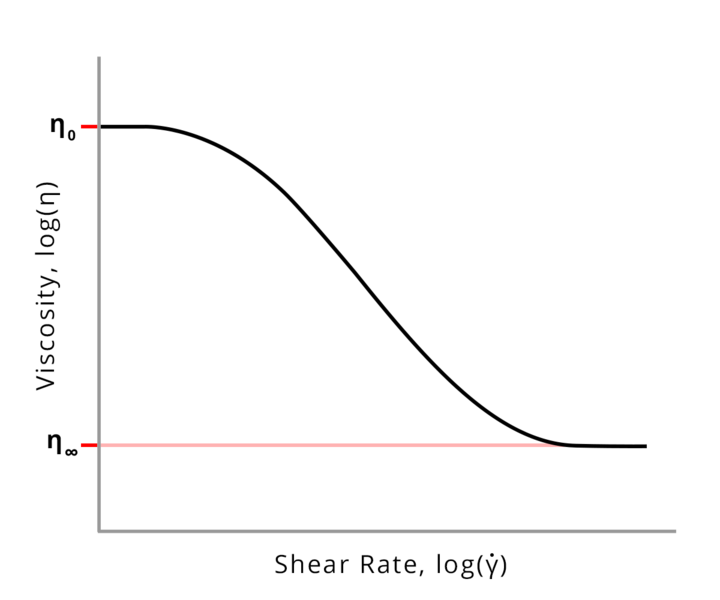
To understand the behavior of a drilling fluid that complies with this thixotropy value, it is necessary to interpret the graph shown previously, in which we will basically analyze what happens to the viscosity of the fluid when it is subjected to shear stress.
It is important to mention that to obtain a thixotropic capacity it is necessary to have a drilling fluid with an apparent viscosity that is in a range of operation where it has a minimum operating viscosity and a maximum operating viscosity as shown in the previous graph, where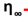 is the minimum viscosity and
is the minimum viscosity and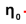 is the maximum apparent viscosity.
is the maximum apparent viscosity.
The important thing about this graph is that we can observe how as we apply a shear stress to the fluid it decreases its viscosity values until it reaches the minimum value of apparent viscosity, where it is very important that it is not less than this value so that it can keep the solids (rock cuttings cut by the drill bit) in suspension.
Thixotropy could be said to be a term where it was originally considered as a reversible isothermal transformation phenomenon from a colloidal solution to a gel, i.e. if a fluid was subjected to a constant temperature, it could have a behavior where it would change from an initial fluid to a gel fluid.
In the case of drilling fluids, the thixotropic phenomenon is caused by clays that arrange themselves in a position of minimum free energy in order to satisfy electrostatic charges.
If we are drilling an oil well with a drilling mud that is considered thixotropic, we have to consider that it is thixotropic if it does not flow, unless it is subjected to an applied stress greater than the gel strength of the mud itself.
In other words it can be interpreted that the gel strength will be transformed at the yield point (τ_0), if the fluid is subjected to a constant shear rate, so the clays contained in drilling mud are graduating and adjusting to the existing shear conditions, on the other hand while this occurs the effective viscosity decreases with time until a constant value is reached, at which point the structure building and structure breaking forces are in equilibrium.
If the shear rate is decreased to the first rate, the viscosity slowly increases until the equilibrium value for this shear rate is reached again. Because of this phenomenon, the original definition of thixotropy has been extended to cover a reversible isothermal change in viscosity with time at a constant shear rate.
As I mentioned in the introduction to the post, there are marked differences between thixotropic and pseudoplastic fluids, so it is important to understand that thixotropy should not be confused with the term plasticity.
What downhole and uphole conditions influence the viscosity of a thixotropic fluid?
[1] Agitation time: this agitation time can be estimated in the laboratory, however if we would like to give an explanation of how a drilling fluid with thixotropic characteristics behaves with respect to time it is necessary to emphasize that the gel properties are activated once the fluid stops circulating in the well and remains static for a considerable time, once circulation is resumed it is important to circulate the fluid again for a considerable time, for example, when I was supervising as operations engineer in the drills in which some wells were drilled in the fields of South Trujillo Lake, one of the qualities that we always kept when ordering the circulation of the fluid, is to circulate increasing the pump pressure gradually breaking gels, until the fluid is conditioned and reaches the initial conditions.
[2] Shear rate: while the drilling fluid is circulating and under constant stress, it can maintain a certain manageable viscosity for the mud pump, this shear rate (pump pressure) is necessary to be applied again at the time of starting the circulation, especially to be able to break gels and that the mud achieves the initial conditions before the well is without circulation.
These thixotropic fluid changes are mainly due to the fact that the structural component changes with time, according to the past shear history of the fluid.
For this reason, thixotropic fluids are said to be "fluids with memory", fluids that have Bingham plastic behavior may or may not be thixotropic, depending on the composition and electrochemical conditions.
A thixotropic test can be performed to the drilling mud in the laboratory, for this it is only necessary to apply a quick thixotropy test can be done with a viscometer containing a recorder X - Y, increasing and then decreasing the speed of the rotor. If a hysteresis ring is obtained in the recorder, then the drilling fluid has thixotropy.
The opposite of thixotropy is reopectance. The viscosity of a rheopectic fluid increases with time at a constant shear rate. In the case of the drilling process, drilling muds that exhibit rheopectic behavior are not used.
Pseudoplastic Fluids
One of the main characteristics of a fluid that is pseudoplastic is that it has no yield point, such behavior can be seen in a graph of shear stress versus strain rate, as shown below:

This figure expresses a curve in which non-linear behavior is seen, although they approach linear behavior when subjected to high shear rates.
For example, if readings taken at high shear rates are extrapolated up to their intersection with the shear stress axis, they may appear to move a yield point similar to that of Bingham plastic fluids, hence their name pseudoplastic fluids.
Suspensions of long-chain polymers are typical pseudoplastic fluids. At rest, the chains are randomly coiled, but they do not build up a structure, because the electrostatic forces are predominantly repulsive.
When the fluid is in motion, the chains tend to align themselves parallel to the direction of flow, this tendency increases as the strain rate increases so that the effective viscosity decreases.
Mathematical model defining the behavior of the consistency curve of a pseudoplastic fluid
The consistency curve of the pseudoplastic fluid flow model is defined by an empirical equation, known as the power law or exponential law, which is expressed as follows:
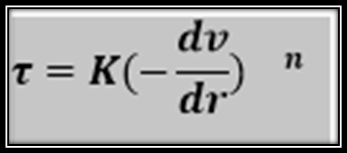
From this equation k and n are constants that characterize the flow behavior of the fluid. K, is the consistency index corresponding to the viscosity of a Newtonian fluid, n is the index of flow behavior, which indicates the degree of departure from flow behavior, which indicates the degree of departure from Newtonian behavior.
Actually the power law describes three flow models, depending on the value of n, among these are:
[1] Pseudoplastic fluid: when n<1, the effective viscosity decreases with strain rate.
[2] Newtonian fluid: when n=1, the viscosity does not change with strain rate.
[3] Dilatant fluid: when n>1, the effective viscosity increases with the strain rate.
Under this point I am going to show you a series of mathematical deductions from the first equation that models the consistency curve of the pseudoplastic fluid flow model, then if we manage to apply logarithm base 10 to both members of the equality of the equation, we are left with:
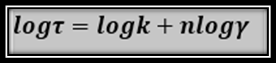
If a plot can be established that manages to model this logarithmic correlation, we could obtain a logarithmic plot of shear stress (τ) versus shear rate (γ), in which a straight line is plotted for fluids that are pseudoplastic.
The plot modeling the behavior of the logarithmic plot is shown below:

In the logarithmic graph of the consistency curve for a fluid based on the power law, we can see how the slope of the straight line defines the value of n, and the intersection on the axis of the shear stress defines the value of k (taking into account that log 1=0), already with the values of k and n, we can substitute the values of n and k in equation nº1 and thus calculate the shear stress to which the fluid is subjected.
The importance of being able to calculate the shear stress, is that from a certain value of shear stress is that the drilling fluid will begin to move to get into circulation after having been in static condition.
However, this value of shear stress that we must generate with the mud pumps on can not be so high, because it would cause mechanical problems in the pump, and can also cause high downhole pressures, thus increasing the chances of fracturing the formation.
Application of some equations for the calculation of n and k
To obtain the values of n and k it is necessary to obtain the viscosity readings in a viscometer called a Fann viscometer, below I show you a Fann viscometer in a laboratory with which these measurements are obtained:

If the intention is to perform the thixotropy design of the drilling fluid, a drilling mud must be prepared in the laboratory with the chemical additives with which the drilling fluid (drilling mud) will be prepared, for example: barite, bentonite, water, among others.
Then we obtain the readings at 600 and 300 RPM in the Fann rotational viscometer, and in this way we can apply the following equation:

Once the value of n is obtained, we can calculate k as follows:

Conclusions
1] Based on the behavior of the flow models, both of fluids that follow Newtonian and non-Newtonian behavior, it is important to highlight that in the graphs and correlations of shear stress versus strain rate there are certain characteristics in the sections of these curves in which they are similar and others in which they differ. For example, the velocity profile of a pseudoplastic fluid has a flattened central portion, it is something like the velocity profile of a fluid that follows the behavior of a plastic Bingham fluid.
2] This article highlights the importance of the study of thixotropy, since it is necessary to know if a drilling mud has the ability to have this gel-like property over time while the mud is at rest, but it must also have the ability to recover the initial conditions once the mud circulation is resumed.
However we can find a very particular behavior for pseudoplastic fluids, for example although pseudoplastic fluids do not have a finite yield point, and consequently no central core of material unaffected by the shear rate, we could conclude that the flattening occurs because, the local shear rate decreases towards the center of the pipe, and the local viscosity increases correspondingly to the flow continuity.
3] Operationally it is very important to take into account the thixotropic capacity of a drilling mud, because if the mud circulation has to be resumed it is very important to circulate it for a long time (until it takes the initial properties), for this it is important that the value of the gels is not very high, because there is danger that when applying very high pump pressure values the formation is fractured and an invasion of drilling fluid into the formation occurs.
4] The thixotropic properties of a drilling mud will depend on certain factors, one of these factors are specific to the structure with which the drilling mud is prepared, for example the amount of bentonite (type of clay) that is added to the mud to achieve the thixotropic property so necessary to keep cuttings (cuttings) in suspension once the drilling mud circulation stops.
Other factors that intervene and can influence for or against the thixotropy of the mud are: the temperature at the bottom of the hole, the capacity of the mud pump to obtain the required pump pressure to be able to break the initial yield point so that the mud can circulate again.
Contribution of this publication to petroleum engineering and the petroleum industry in general
Thixotropy plays a fundamental role in the preparation of drilling fluids, since without this thixotropic capacity it would be impossible to drill an oil well, it is important to mention that the study of thixotropy is closely related to fluids that follow a plastic behavior, i.e. those fluids that deform when a certain shear stress is applied to them.
In this article, some graphical deductions supported with mathematical correlations can be obtained that help in the understanding of certain calculations necessary to achieve the shear stress required for these plastic fluids to have a flow on par with a plastic fluid.
For anyone who wants to inquire about the importance of employing a drilling mud with thixotropic properties in the drilling activities of an oil well, you can start with reading this post, as you can find the combination of field application examples, while at the same time you can analyze the considerations that are made by reason of certain graphs and mathematical models, which help to predict the flow behavior of drilling muds with plastic characteristics and its counterpart which are pseudoplastic fluids.
This post may provide a creative idea in the readers to investigate about what other fluids follow pseudoplastic (thixotropic) behavior and maybe they can mention in the comments what is this fluid and what importance do they have in the field of application?
I hope I have addressed certain aspects of thixotropy that may be of interest to the scientific and academic community of the hive platform.
Observations
- The cover image has the following Image Source and was edited using Microsoft PowerPoint design tools.
References
!wine
Cheers, @ranathunga You Successfully Shared 0.100 WINE With @carlos84.
You Earned 0.100 WINE As Curation Reward.
You Utilized 2/3 Successful Calls.
WINE Current Market Price : 1.100 HIVE
Thank you for your support. Regards
It's refreshing to read an article like this. Thanks for sharing.
Thank you for your rating and for your positive comment. Regards