¿Cómo calcular la masa de una lámina plana simétrica de densidad variable con integrales dobles?

Hola amigos de la plataforma hive.
En esta oportunidad quiero explicarte cómo puedes calcular la masa de una lámina plana simétrica de densidad variable, para ello es importante que te ubiques en libro de cálculo con Geometría analítica de Larson Volumen II en la página 1243 y veamos el siguiente ejemplo:
Hallar la masa de la lámina correspondiente a la región parabólica: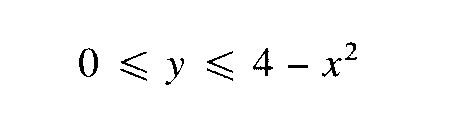 Si la densidad de la lámina es
Si la densidad de la lámina es
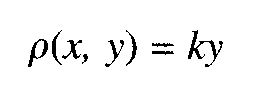
Calcular la masa de la lámina plana y simétrica de densidad variable.
Solución
Lo primero que debemos hacer es basarnos en la fórmula para calcular la masa de una lámina plana de densidad variable con integrales dobles:
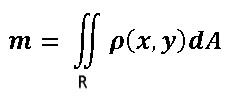
De donde de la expresión anterior:
m = es la masa del región de la lámina plana de densidad variable, que para el caso del ejercicio es una lámina plana simétrica que luego explicare porque es simétrica.
R = es la región del plano (x,y) que limita para este caso la región parabólica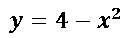
Para saber exactamente la región R que vamos a definir, voy a graficar la parábola 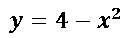 con el software geogebra y posteriormente lo voy a editar para mostrarlo a continuación:
con el software geogebra y posteriormente lo voy a editar para mostrarlo a continuación:
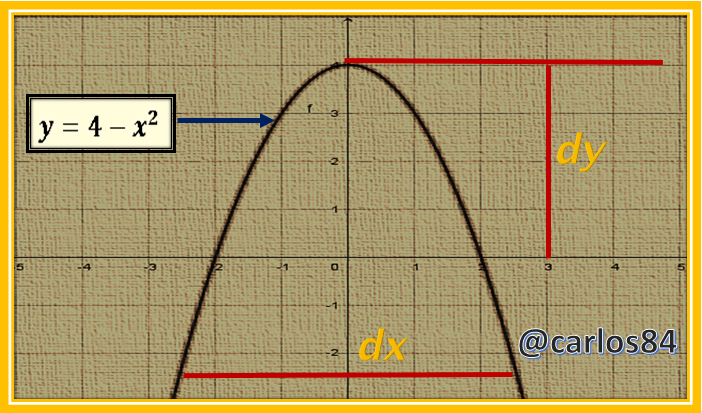
Como se puede observar el diferencial de y está limitado desde la distancia existente desde el eje x hasta la función parabólica, por lo que la región R está limitada por el eje y de la siguiente manera:
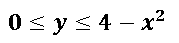
El diferencial de x está limitado por la distancia que existe desde -2 hasta 2, esto lo que quiere decir es que la gráfica es simétrica con respecto al eje y, razón por la cual podemos tomar la mitad de la región limitada y multiplicar por 2. La región R limitada por la función parabólica en el eje x queda de la siguiente manera:
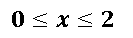
El planteamiento de la integral para calcular la masa de la lámina plana simétrica de densidad variable es:
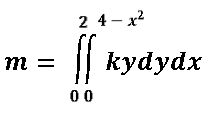
Lo importante y que tenemos que recordar en este ejercicio es que el resultado que nos de la masa la tenemos que multiplicar por 2, ya que como la gráfica es simétrica respecto a y estamos agarrando la mitad.
Como k es una constante la sacamos fuera de la integral tal y como sigue:
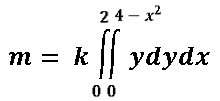
Luego integramos respecto a la variable y y posteriormente aplicamos el teorema fundamental del cálculo:
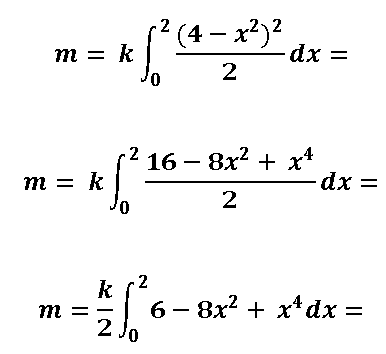
Cuando se aplicó el teorema fundamental del cálculo no se sustituyó el límite inferior ya que da 0, también el 1/2 se saca como una constante y queda k/2 multiplicando fuera de la integral, lo otro importante es que se resolvió el producto notable elevado al cuadrado.
Ahora solo queda realizar la integral respecto a la variable x y aplicamos el teorema fundamental del cálculo sólo sustituyendo el límite superior igual a 2, ya que el límite inferior es igual a 0, y cuando hagamos la sustitución nos dará 0. La resolución de esta integral queda como sigue:
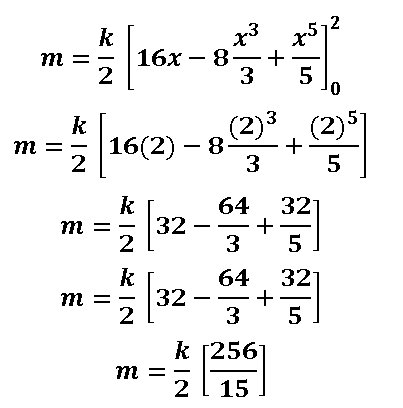
Pero como se dijo anteriormente, como la gráfica es simétrica respecto a y tomamos en cuenta la mitad de la región R, por lo que debemos multiplicar el resultado final por 2:
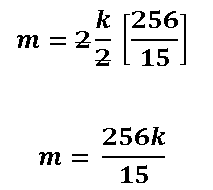
Finalmente nos queda que la masa de la lámina plana y simétrica de densidad variable es 256k/15, en donde el factor k el significado que tiene es que k va a ser mayor en los puntos en donde la región R de la parábola tenga mayor densidad, entonces la masa será mayor, pero siempre a una proporción de 256/15.
En esta primera parte aprendimos a calcular la masa de una lámina plana simétrica de densidad variable por medio de una integral doble, posteriormente en otros post siguiendo esta misma serie temática aprenderemos a calcular el momento de inercia y centro de masa (centroide) de una lámina plana de densidad variable.
Observaciones
- Todas las imágenes son de mi autoría, las ecuaciones fueron elaboradas utilizando las herramientas de diseño de Microsoft Word, las otras dos imágenes fueron realizadas apoyándome en el software geogebra 5.0 y las herramientas de diseño de Microsoft PowerPoint.
Referencia consultada y recomendada
Cálculo (completo) Vol 1 y 2 9na Edición Ron Larson & Bruce H. Edwards
https://twitter.com/CARLOSJB84/status/1366632479000567814
Su post ha sido valorado por @ramonycajal
Gracias por el apoyo @ramonycajal y a @cervantes. Saludos
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Gracias por el apoyo amigos de StemSocial. Saludos
Muy buen material amigo @carlos84, este tipo de recursos son muy adecuados como guía para los estudiantes, pudiendo observar así el uso que tienen las integrales. Saludos!
Hola @emiliomoron.
Gracias amigo, te cuento: ya hoy supe el sexo de mi bebe, y es niña según lo que arrojo el ecograma. Saludos amigo y gracias por tu comentario.