¿Cómo calcular el área de un triángulo con integrales?
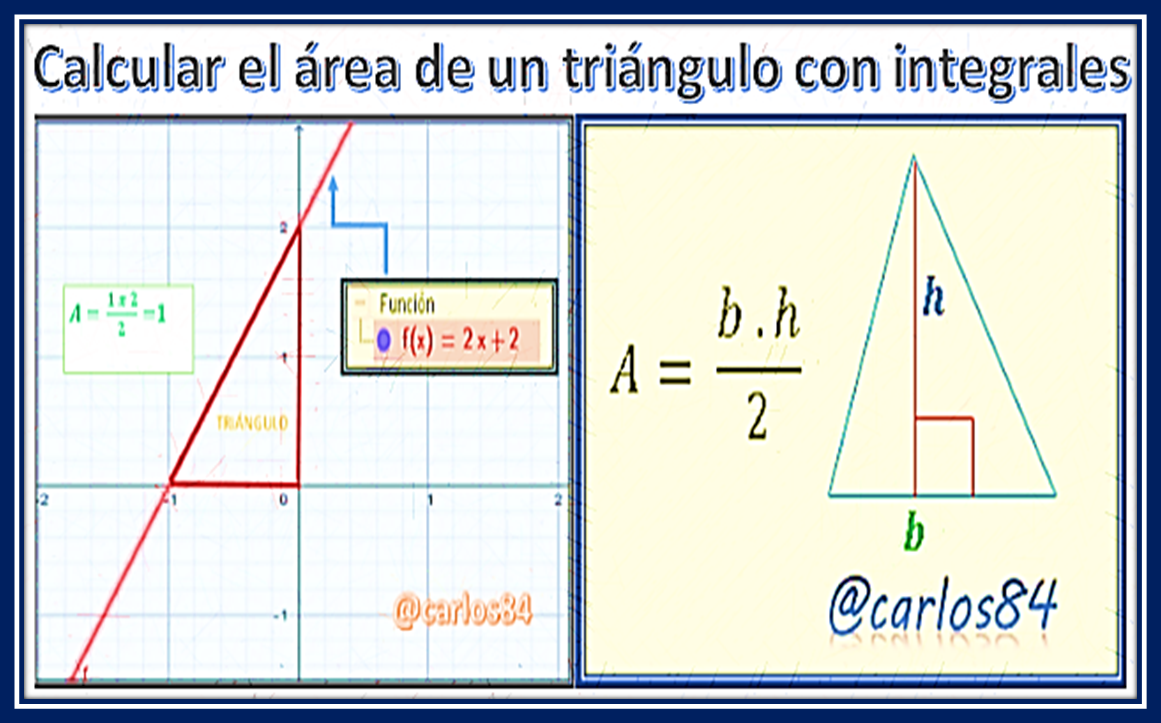
En esta oportunidad quiero compartir con todos ustedes una forma alternativa un poco más compleja para calcular el área de un triángulo, sin embargo a pesar de que es una forma compleja es muy importante conocerla ya que nos puede ayudar a desarrollar nuevas formas demostrativas y a la final conocer otras alternativas diferentes a las tradicionales.
Como todos sabemos el área de un triángulo se calcula de la siguiente forma:
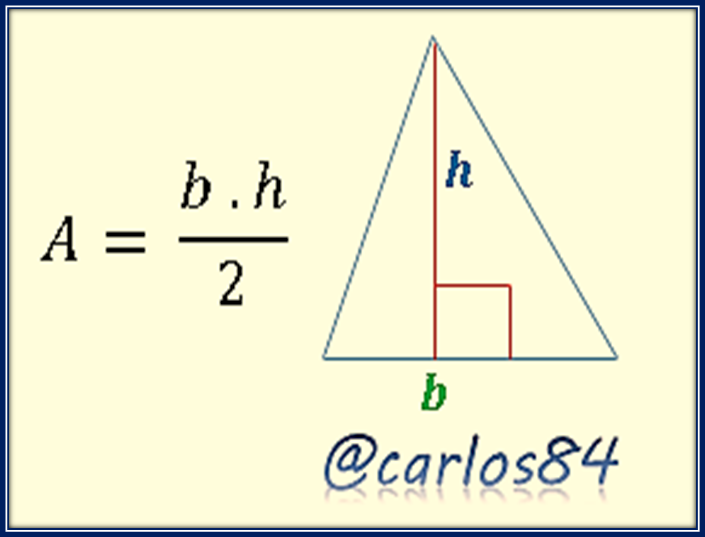
En donde b es la base del triángulo y h es la altura del mismo.
Ahora bien quizás te preguntes:
¿Cómo de una forma bastante sencilla puede existir una más compleja para calcular el área de un triángulo?
Esta es una respuesta muy sencilla, ya que los que de alguna manera han leído mis post se habrán podido dar cuenta que mediante las aplicaciones de la integral se puede calcular el área bajo la curva, es decir se puede calcular el área que forma una función con el eje x del sistema de coordenadas cartesiano.
Es por ello que el ejemplo que las traigo a continuación es el siguiente:
Calcular el área que está definida por la función lineal:
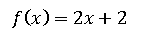 el eje x y el eje y.
el eje x y el eje y.
La región del plano cartesiano que representa esta zona se las presento a continuación:
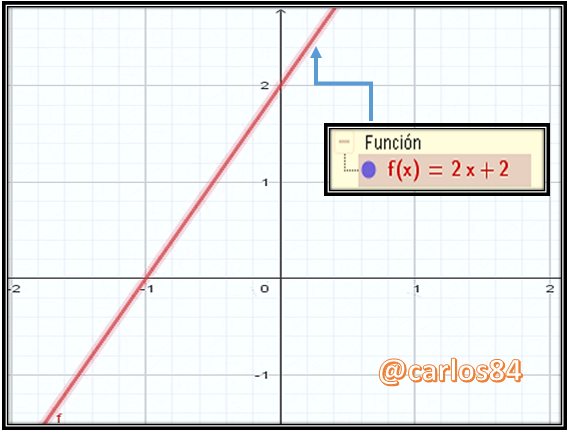
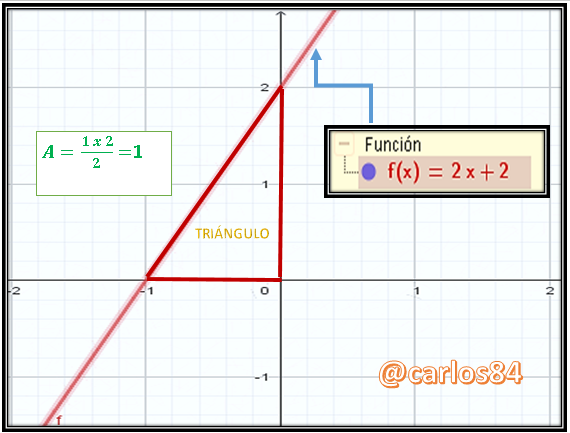
Si calculamos el área de forma tradicional, tal y como se nos ha enseñado según los conceptos de geometría analítica el área del triángulo es igual a 1.
La gran interrogante es:
¿Nos dará el mismo resultado si la calculamos mediante la aplicación de la integral?
Veamos para aplicar la aplicación de la integral para el cálculo de área procedemos de la siguiente manera:
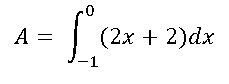
Para resolver la integral planteada primeramente resolvemos la integral indefinida y después aplicamos el teorema fundamental del cálculo:
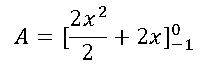
Cuando se aplica el teorema fundamental del cálculo es porque se sustituye el límite inferior menos la sustitución del límite superior, por lo tanto queda de la siguiente manera:
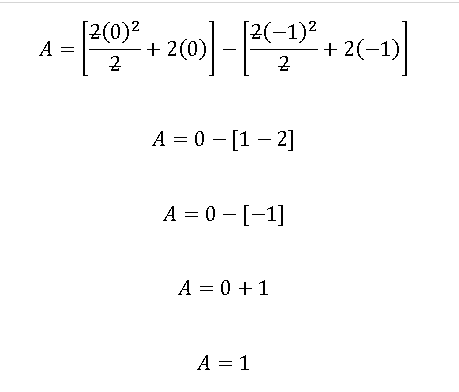
Como pudimos apreciar ciertamente el área de un triángulo se puede calcular empleando como herramienta las aplicaciones de la integral para calcular área, de esta forma podemos ampliar más nuestros conocimientos demostrativos y poder discernir sobre otras herramientas que nos ayudan a calcular áreas de diferentes figuras geométricas.
Referencias recomendadas para ampliar el conocimiento del cálculo
Observaciones
Todas las imágenes son de mi autoría y fueron elaboradas empleando las herramientas de diseño de Microsoft PowerPoint y el software geogebra 5.0
Su post ha sido valorado por @ramonycajal
Gracias por el continuo apoyo a @ramonycajal. Saludos y bendiciones para ti.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Gracias por el apoyo al equipo de Stemsocial. Saludos
Hola @carlos84, su post acerca lo complejo que pudiera ser una integral, ya definida como el área de una curva, y el cálculo del área de un triángulo, como demostración. Gracias