Saludos amigos de #STEM-espanol, en esta ocasión abordaremos una solicitación muy común en la ingeniería estructural: la fuerza cortante. Los diagramas de fuerza cortante se utilizan para representar gráficamente la manera en que se comporta esta solicitación a lo largo de un elemento.

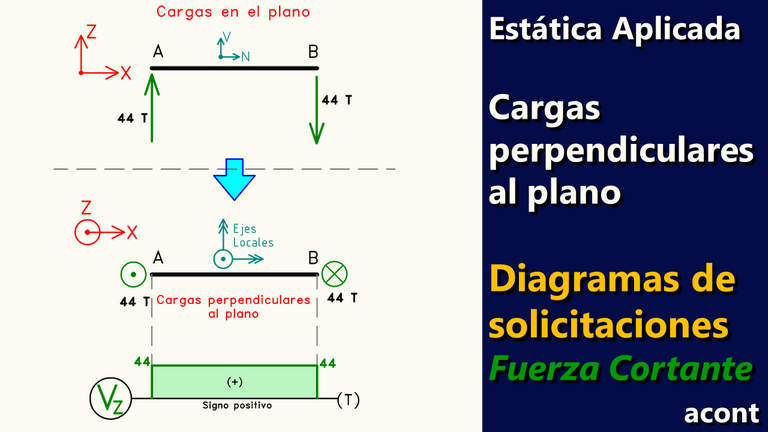
Ya abordamos en la anterior publicación el caso del diagrama de momento torsor. La fuerza cortante tratada en esta publicación se refiere a la misma fuerza de corte que actúa en sistemas tradicionales (con cargas en su plano). En el caso de cargas perpendiculares al plano, solo varía la manera en que se representa esta fuerza.

Normalmente se representa a la fuerza de corte como un vector, tal como cualquier fuerza. Pero cuando tratamos con cargas perpendiculares al plano, esta "flecha" o vector no se puede representar adecuadamente, ya que pasamos de observar este vector "de frente" a observarlo "desde arriba" (plano X-Y). Esta fuerza de corte actúa en dirección del eje "Z", por lo que se verá como un punto, por consiguiente, cambia su simbología.

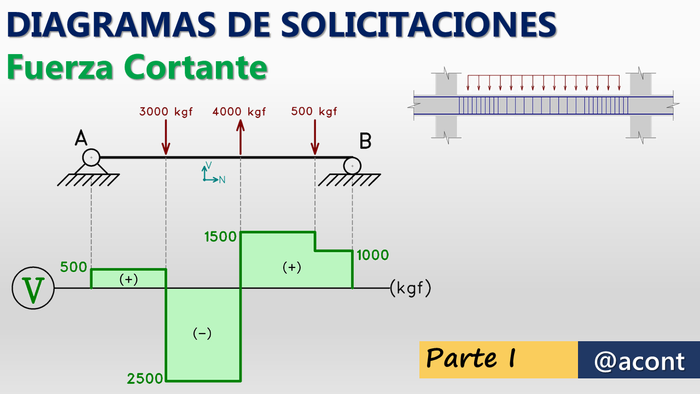
Los principios que rigen esta fuerza de corte son los mismos que ya abordamos en sistemas con cargas en su plano: Diagramas de Solicitaciones: Fuerza Cortante Parte I y Diagramas de Solicitaciones: Fuerza Cortante Parte II:

---

La única diferencia radica en la manera de representar las cargas puntuales y distribuidas, lo cual abordaremos en esta publicación con más detalle.

Abordaje cualitativo (gráfico)

Antes de abordar aspectos matemáticos, es adecuado mostrar como se puede determinar gráficamente el diagrama de fuerza cortante de acuerdo a la convención de signos que poseemos. Esto nos permite graficar este diagrama en la mayoría de los casos, en donde la complejidad de las cargas externas no es tan alta cmo para ameritar el empleo del cálculo.

Caso simple: sin cargas externas

De acuerdo a la convención de signos, es bastante evidente y simple el signo que tomará el diagrama de fuerza cortante:

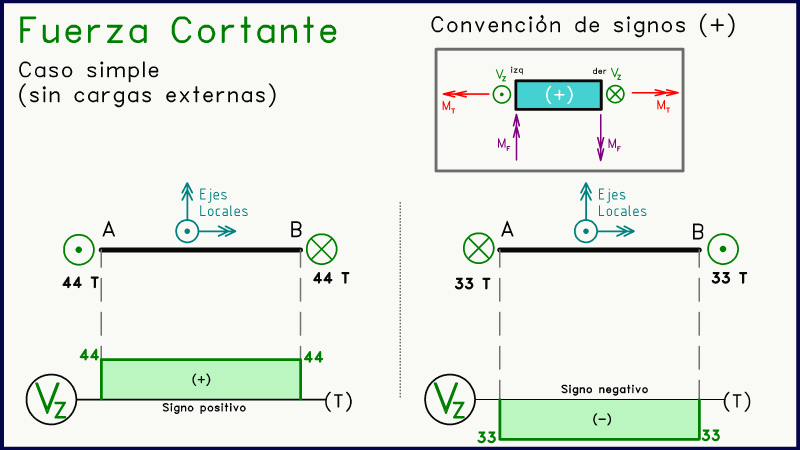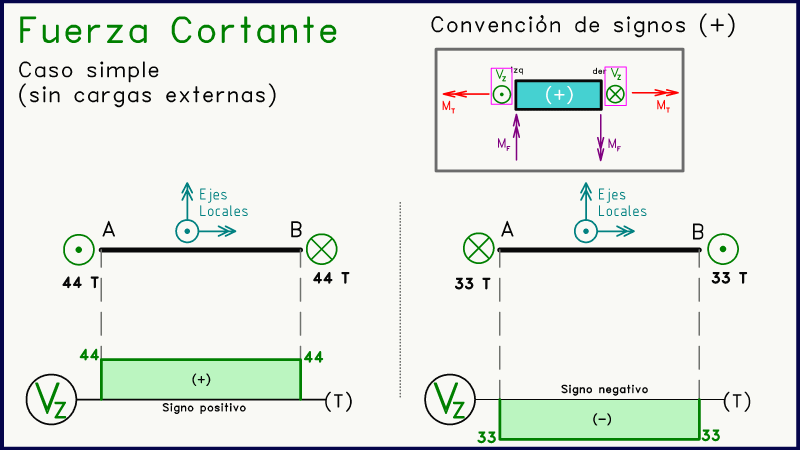
En este caso es bastante simple. Por equilibrio estático, la fuerza de corte debe ser igual en magnitud y en sentido contrario en ambos entremos del elemento. Solo hay dos opciones: una resultará en un diagrama rectangular positivo y otra en uno negativo, dependiendo del sentido de las fuerzas de corte ("punto"-"equis" ó "equis"-"punto").

Con carga externa puntual

Otro caso muy frecuente es cuando aparece una carga puntual externa en algún punto intermedio del elemento. La presencia de una fuerza puntal (en la misma dirección que las fuerzas de corte) generará en el diagrama de corte un salto vertical.

Este salto será hacia arriba en caso de que la fuerza puntual externa se dirija en sentido positivo (punto), y hacia abajo si la fuerza externa tiene dirección negativa (equis).

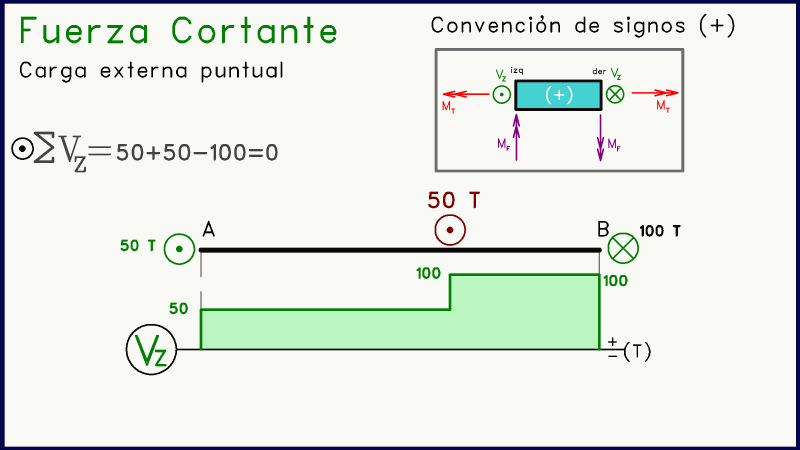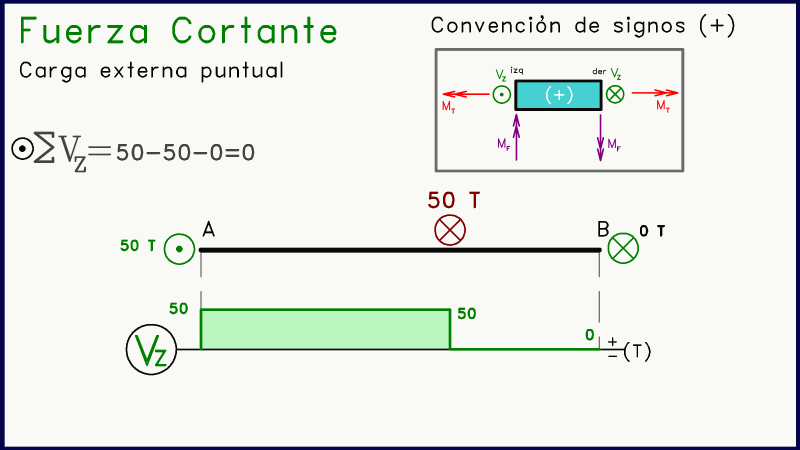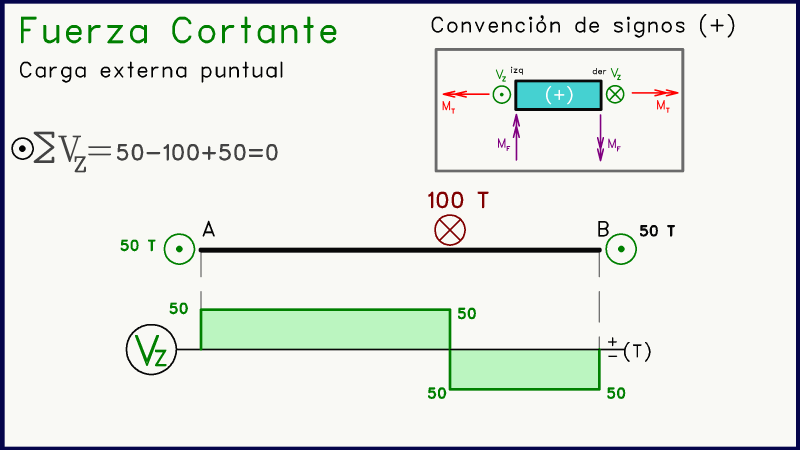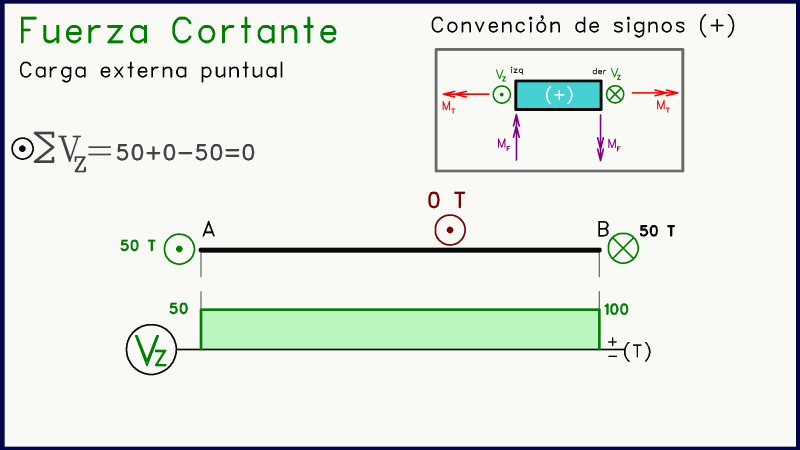
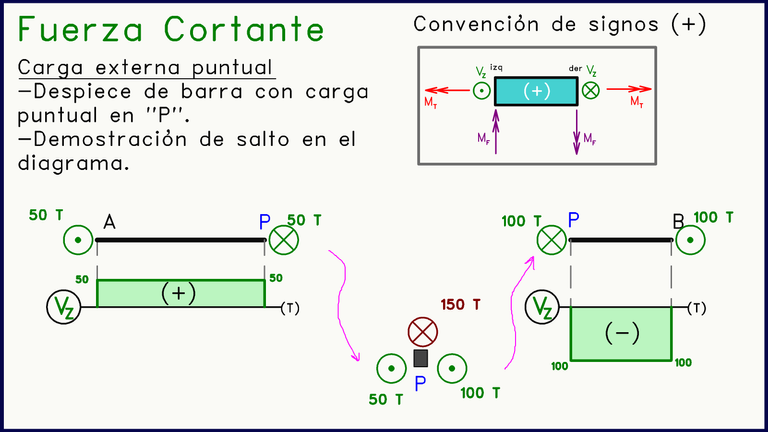
Tal como sucedía en la anterior publicación, donde se realizó un despiece que evidenciaba el equilibrio interno del momento torsor, es más fácil de demostrar o entender el porqué de este salto si realizamos un despiece del elemento, separando el punto infinitesimal donde se aplica la carga externa puntual:

Con carga externa distribuida

Este caso es también bastante común. Usualmente se encuentran las cargas distribuidas como un conjunto unido de flechas que actúan en grupo, señalando que la carga externa no es puntual sino que se aplica a lo largo de una longitud dada del elemento.

El caso más común es el de una carga distribuida de valor uniforme o constante, ya sea positiva o negativa. Su representación se da como se muestra en la siguiente animación.

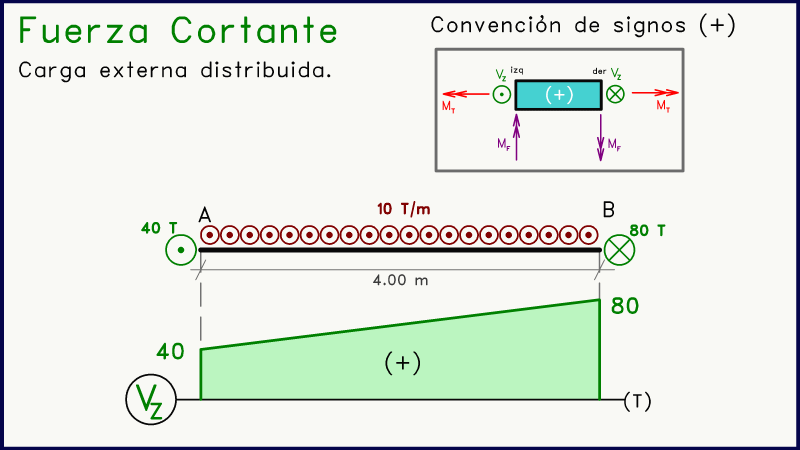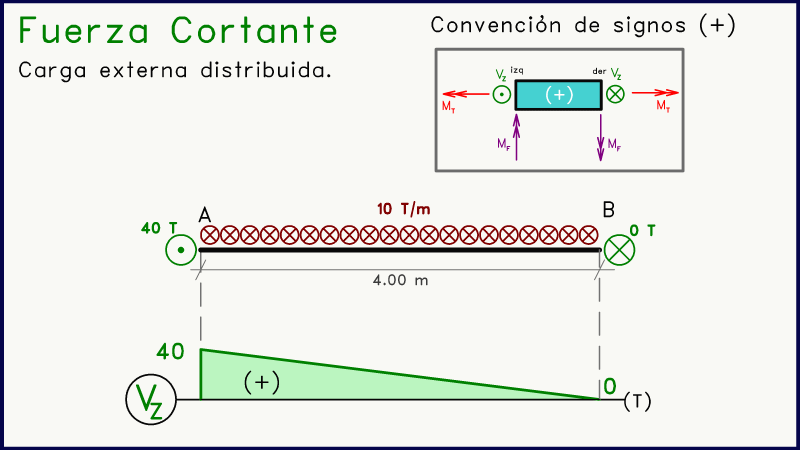
Su efecto es el de generar en el diagrama de corte una variación lineal de la magnitud de esta solicitación. Puede ser con pendiente positiva si la carga distribuida se orienta de manera positiva, o viceversa.

Usualmente es fácil de representar gráficamente, pero en ocasiones es mejor realizar el abordaje matemático a través del cálculo para una graficación más precisa.

Otro caso común es el de cargas distribuidas trapezoidales o triangulares. En este caso, la carga distribuida tiene un valor que no es constante. Suele ser necesario el empleo del cálculo, ya que así se puede determinar de manera precisa cómo se comporta el diagrama de corte, el cual tendrá un comportamiento parabólico.

Método cuantitativo (analítico)

Para el abordaje matemático solo necesitaremos una ecuación:

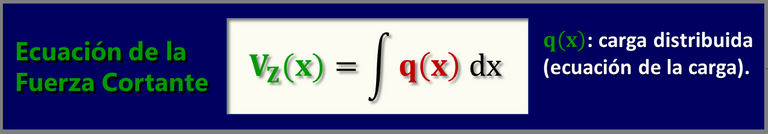
Esta ecuación implica de antemano conocer cuál es la ecuación que define a la carga externa: q(x). Hay ocasiones en las que es fácil de determinar, ya sea porque no hay carga externa o es de valor constante, tal como veremos a continuación:

Caso simple

Si no existen cargas externas (q(x)=0), entonces el resultado de la integral es una constante (similar al caso simple de arriba). Y dicha constante es igual al valor de la fuerza cortante en los extremos, la cual es ya conocida del despiece de la estructura.

Cargas puntuales externas

Si existen fuerzas puntuales externas, se realiza la división en intervalos, y en cada uno de ellos se da el caso simple (ya abordado arriba). En el lugar de cada fuerza puntual se produce un salto en el diagrama.

Carga distribuida constante

El valor de la ecuación de la carga será q(x)=±q, es decir, será un valor constante positivo si la carga distribuida se dirige en dirección positiva (puntos) o un valor constante negativo si se dirige en dirección "Z" negativa.

El resultado de la integral será la ecuación de una recta, donde el valor inicial es ya conocido (valor de la fuerza cortante en el extremo izquierdo).

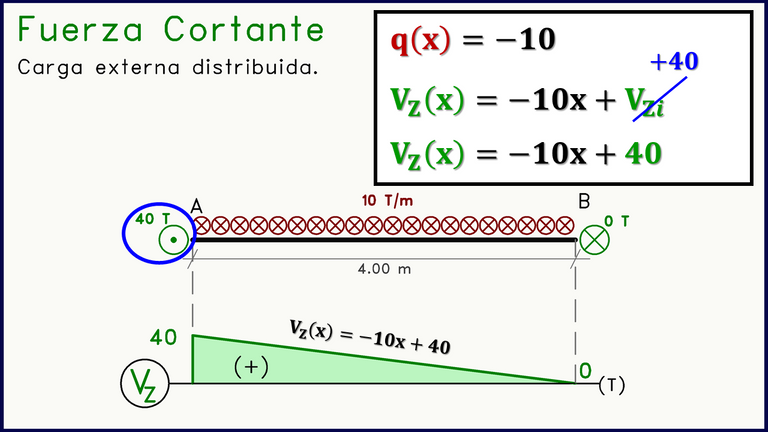
Carga distribuida variable o trapezoidal

Este es el caso de carga externa más complejo, y tal como en el caso del momento torsor, es necesario primero construir la ecuación que define a la carga distribuida externa.

En la publicación mencionada arriba (Parte II de los diagramas de fuerza cortante en sistemas con cargas en el plano), se describió con mucho mayor detalle como construir la ecuación de la carga q(x)=ax+b.

En la siguiente imagen, se describe de manera general cómo realizar este procedimiento, puesto que los principios son los mismos, solo que las cargas distribuidas presentan una simbología diferente, producto de su orientación perpendicular a plano.

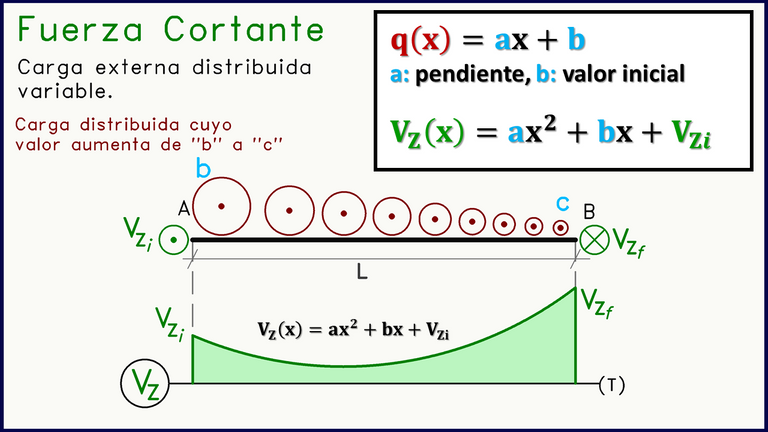
Se deben hallar los valores "a" y "b" de la ecuación de la carga q(x)=ax+b para luego integrarla y hallar la ecuación que define al diagrama de fuerza cortante.

"a" representa a la pendiente de la carga distribuida trapezoidal (o triangular), y suele ser un poco difícil de asimilar esto en el dibujo ya que las cargas se ven desde "arriba" y no de frente. Sin embargo, los círculos que se utilizan de símbolo, suelen incrementarse simbólicamente en tamaño cuando se presenta una carga de este tipo, por lo que esta "pendiente" es más fácil de ver. El signo de este factor dependerá de lo que se obtenga en el procedimiento dado.

"b" representa al valor inicial de la carga distribuida en el extremo izquierdo o inicial del intervalo (puede que la carga distribuida no empiece en el extremo izquierdo de la barra sino más a la derecha). Si signo es positivo si la carga distribuida tienen orientación positiva (punto).

---

La solicitación de fuerza cortante es muy importante en el ámbito de la ingeniería estructural, y puede darse su análisis tanto en el ámbito usual como en otra proyección, como es el caso de estructuras con cargas perpendiculares al plano.

A continuación, abordaremos un ejemplo para la elaboración de los diagramas de fuerza cortante en el siguiente caso de cargas:

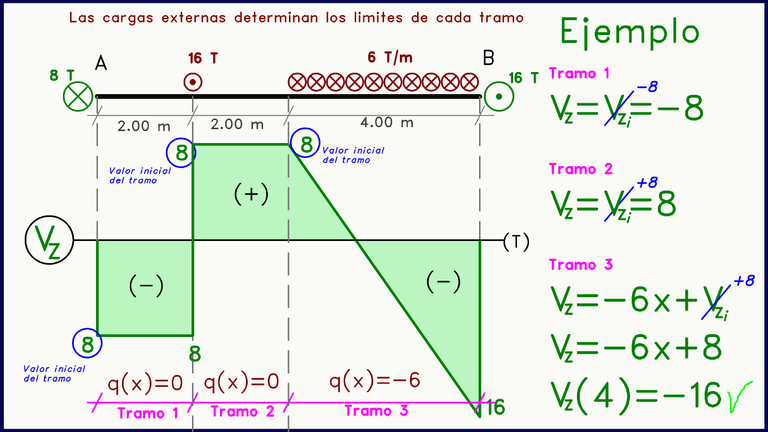
En el ejemplo observamos que cada carga externa determina los límites de cada tramo, por lo que cada uno de los tramos posee una ecuación matemática distinta para el diagrama de fuerza cortante. La ecuación es el resultado de integrar la ecuación de la carga distribuida externa, la cual puede ser nula o tener cierto valor.

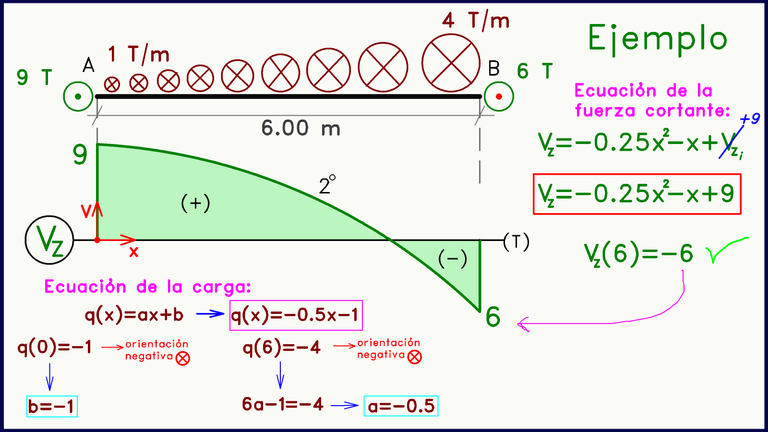
En el siguiente ejemplo, abordamos el caso de una carga distribuida trapezoidal, el cual representa mayor complejidad, al tener que hallar la ecuación que define a la carga distribuida.

Aportes de esta publicación

Se introduce al desarrollo de los diagramas de fuerza cortante en el caso de estructuras con cargas perpendiculares al plano, mostrando cómo intervienen las cargas externas en el comportamiento de esta fuerza interna dentro de un elemento. De esta manera, se adquiere un buen manejo de esta herramienta, no solo en sistemas con cargas en el plano sino también en otra proyección, donde se requiere de una perspectiva distinta, aunque los principios sean los mismos.

Referencias

•Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 202-208)._Fuente

---

Publicaciones anteriores

•Introducción a las estructuras con cargas perpendiculares al plano | Estática Aplicada

•Equilibrio de estructuras con cargas perpendiculares al plano — Parte I (Introducción)

•Equilibrio de estructuras con cargas perpendiculares al plano — Parte II (Cálculo de reacciones externas)

•Equilibrio de estructuras con cargas perpendiculares al plano — Parte III (Cálculo de reacciones externas)

•Equilibrio de estructuras con cargas perpendiculares al plano — Parte IV (Despiece)

•Estructuras con cargas perpendiculares al plano — Barras inclinadas y proyección de reacciones

•Estructuras con cargas perpendiculares al plano — Diagramas de Solicitaciones (Introducción)

•Estructuras con cargas perpendiculares al plano — Diagramas de Momento Torsor

---

Imágenes de autoría propia realizadas mediante LibreCAD y PowerPoint. GIFs elaborados mediante Photoscape.

Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.

---

¡Gracias por visitar! — ¡Thanks for visiting! @acont