Estática Aplicada. Diagramas de Solicitaciones: Momento flector Parte I
En cualquier ámbito relacionado a la física, especialmente en el estudio del equilibrio (estática), la palabra “momento” o “par” tiene buenas probabilidades de aparecer.
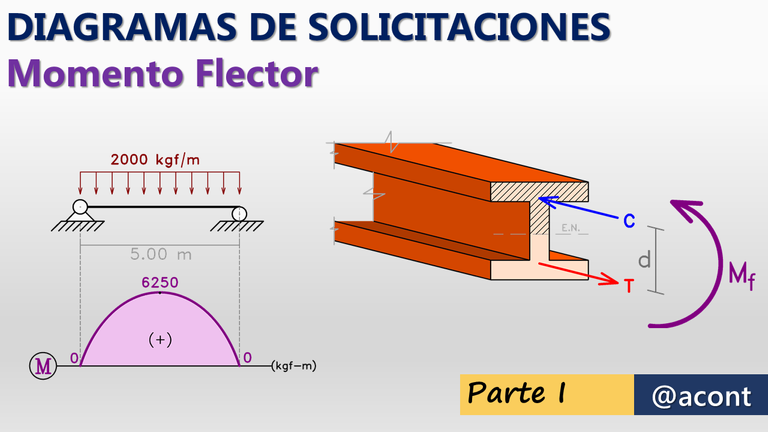
En Ingeniería Civil, sin embargo, el momento se suele relacionar con frecuencia a la solicitación o carga interna que se desarrolla dentro de los elementos estructurales (momento flector). Ya veremos a que se debe esta denominación.
En esta serie de publicaciones dedicada a los diagramas de solicitaciones, nos encontramos abordando la última de las tres solicitaciones más importantes en el plano:
•Diagramas de fuerza axial (N).
•Diagramas de fuerza cortante (V).
•Diagramas de momento flector (Mf).
•Aplicaciones prácticas de los Diagramas de Solicitaciones.
•Metodología para elaborar los diagramas de solicitación ante cualquier sistema de cargas.
Todo el material sobre Estática Aplicada se ha recopilado en la siguiente publicación:
Material de Estática Aplicada
Introducción |
El momento flector es probablemente la solicitación de mayor importancia en el análisis y diseño estructural. Dejando por fuera algunos otros parámetros y condiciones, es dicha solicitación la que dicta cuanto acero longitudinal tendrá una viga de concreto armado o cuál será el tamaño de una viga de acero estructural.
Si nos referimos al momento de una fuerza genérico, tal como en Física básica, tendremos simplemente el producto vectorial de dos vectores.
El caso más común en la vida diaria, se da al momento de empujar una puerta para abrirla o utilizar una llave para apretar una tuerca. Nuestra fuerza es un vector que tiene magnitud y dirección. También tenemos un radio vector o “brazo” que representa a la puerta o a la llave y tiene su origen en el pivote o punto de giro.
Ambos vectores conforman un plano, y el producto vectorial entre ellos es un vector que es perpendicular a ambos o al plano que forman. Este vector es el momento de una fuerza. A pesar de ser un vector con dirección dada, su efecto es el de causar un giro. Es por ello que en la Fig. N°1 observamos su representación como una “flecha que gira”:
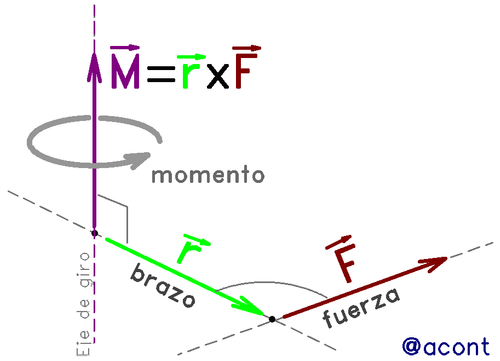
La representación usual del momento en Estática Aplicada es la de una “flecha que gira”. Esto significa que se indica como una carga que “gira”, y no estamos tomando en cuenta u obviando la fuerza y el “brazo” que la genera.
El momento y el momento flector en Estática Aplicada |
Ya que esta publicación se enfoca en la Estática y no en la Física o en el análisis estructural, es necesario aprender ciertos conceptos básicos. Debemos diferenciar el momento (carga externa aplicada a sistemas isostáticos) del momento flector (solicitación).
El momento en sistemas isostáticos es una carga que forma parte del sistema de cargas externo. Se representa, como ya sabemos, mediante una flecha curva con un sentido de giro específico. Se aplica, al igual que una fuerza puntual, en un punto determinado (Fig. N°2).
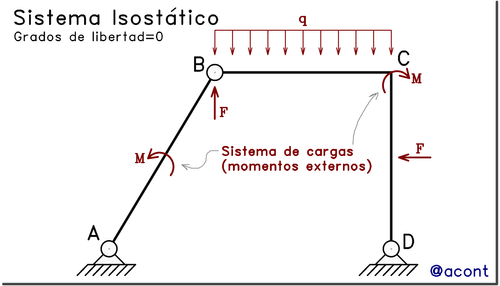
Al mismo tiempo, suelen surgir algunas dudas prácticas sobre su representación ¿Alguna vez usted ha visto una especie de “fuerza giratoria” en estructuras de la vida real?
En realidad, es poco común que alguna carga externa se presente como un momento o fuerza que tiende a hacer girar un elemento estructural en determinado punto. No obstante, estudiar el momento como carga externa no está demás en el ámbito académico.
Por otra parte, tenemos cargas internas o solicitaciones que si pueden generar este efecto de “giro” en un elemento. Aquí es donde entra en juego el momento flector. Para entender mejor esto, analizaremos un sistema isostático sencillo: una viga simplemente apoyada sometida a dos casos de carga (Fig. N°3):

Vamos a analizar este sistema de dos maneras: primero, realizaremos un enfoque desde el punto de vista académico, donde tenemos un sistema isostático y realizaremos un corte en determinado punto para analizar sus fuerzas internas (solicitaciones) mediante las ecuaciones de equilibrio estático; luego, analizaremos esta viga tal como si formara parte de un sistema estructural real, donde podremos apreciar su deformación.
Realizando un corte en el sistema isostático: carga puntual
En primer lugar, debemos recordar que en la Estática, se estudia el equilibrio de los cuerpos, asumiendo que los mismos son rígidos (chapas). No se admite deformación en los sistemas isostáticos.
Realizaremos un corte en un punto arbitrario, situado a una distancia “x” del extremo izquierdo de la viga. Producto del corte, podemos apreciar las reacciones internas que aparecen allí, las cuales deben existir para garantizar el equilibrio de fuerzas del subsistema o porción de la viga (Fig. N°4).
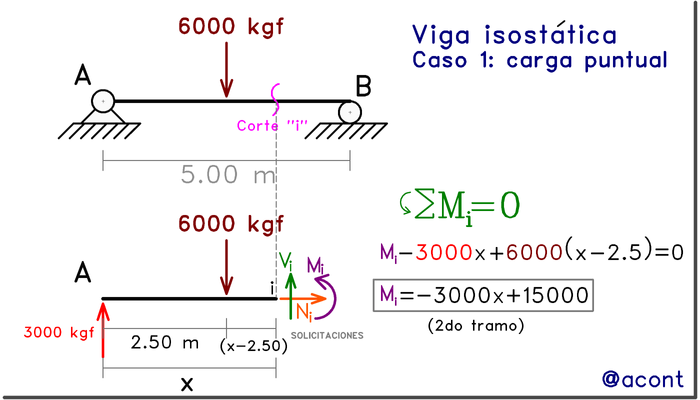
Una de estas reacciones internas es un momento, el cual pasa a denominarse momento flector al ser una solicitación o fuerza interna. Este momento debe existir para que la porción de la viga a ambos lados del corte esté en equilibrio de momentos (sumatoria de momentos igual a cero).
Un análisis de la ecuación obtenida, nos muestra que el momento flector alcanza su valor máximo cuando x=2.50 m. Es decir, el momento es máximo en el punto donde la fuerza puntual es aplicada. También podemos observar que M=Mf(x) es una función lineal.
La ecuación del momento flector cambiará siempre que existan fuerzas puntuales o cambios en la carga distribuida, haciendo que sea necesario realizar un corte en cada tramo o intervalo. Si realizamos otro corte antes de la carga puntual, obtendremos una ecuación distinta. El diagrama de momentos flectores se muestra en la siguiente figura.
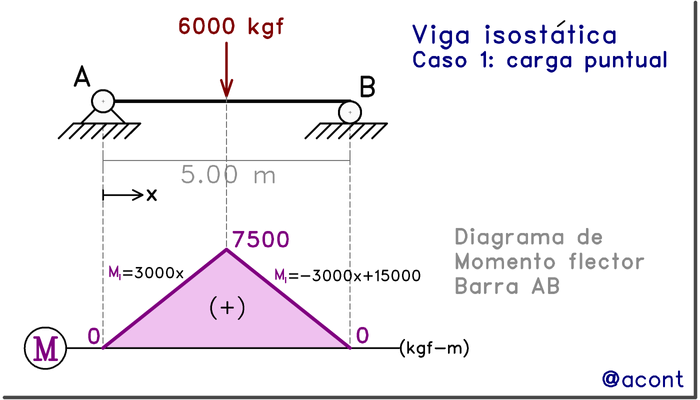
Es por ello que el Diagrama de momentos flectores nos facilitará la tarea de visualizar la magnitud de esta solicitación a lo largo de todo el elemento cuando empleemos un método similar al utilizado en las publicaciones sobre las fuerzas axial y cortante.
Realizando un corte en el sistema isostático: carga distribuida
Para el caso de la carga distribuida, no tendremos dos tramos con ecuaciones distintas, ya que no existen discontinuidades en todo el dominio. Simplemente realizaremos un corte en cualquier punto, alejado una distancia x del extremo izquierdo.
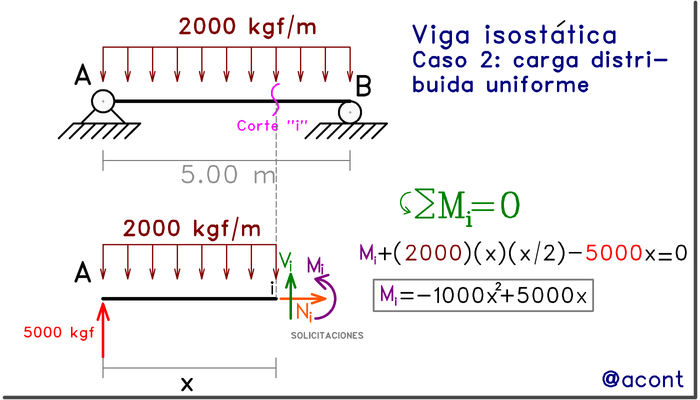
La ecuación obtenida nos dice que el momento presenta un comportamiento cuadrático de 2° grado, es decir, posee forma parabólica.
También cabe destacar que las condiciones de vinculación (articulación fija y apoyo simple) nos brindan puntos en los que la restricción de rotación no existe. Esto significa que el momento debe ser nulo en dichos puntos. Esto lo podemos comprobar evaluando la ecuación M(x) para x=0.00 m y para x=5.00 m.
Finalmente, el diagrama de momentos flectores se grafica de la siguiente manera:
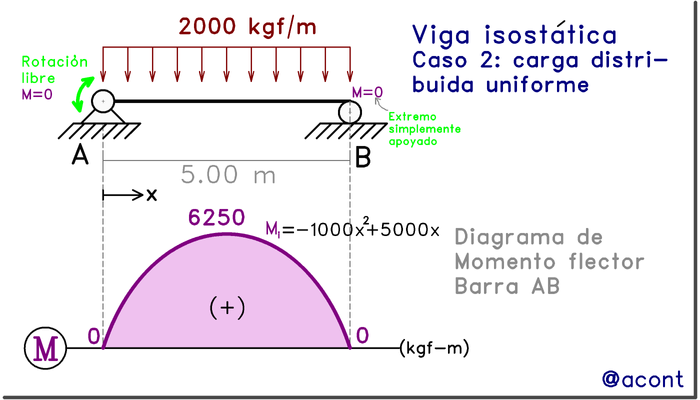
Esta manera de graficar el momento flector se basa en la aplicación de las ecuaciones de equilibrio estático en cada punto de corte, por lo que en posteriores publicaciones abordaremos una manera más efectiva de abordar el momento flector.
Viga real: estructuras deformables. Origen del término “flector”
Saliéndonos del ámbito de la Estática y entrando un poco en deformaciones y esfuerzos, temas un poco más avanzados en el estudio de Ingeniería Civil, podremos visualizar el origen del término flector. Visualicemos la deformación de la viga ante la carga puntual (Fig. N°8).
Ya sabemos que el momento flector máximo se encuentra justo en el punto donde la carga puntual se aplica. Analicemos dicho punto más de cerca:
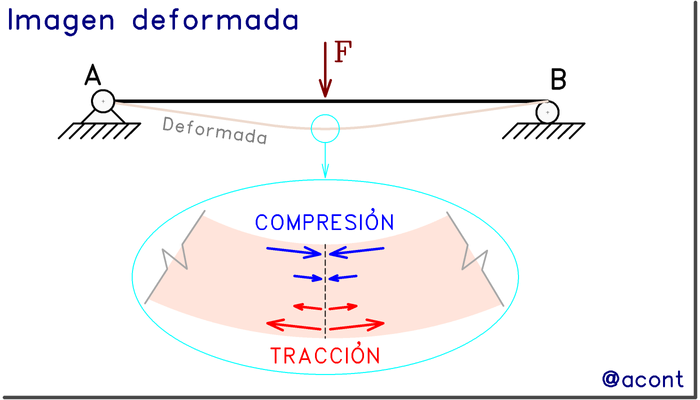
Producto de la carga puntual, la viga se deforma o flexiona hacia abajo. En dicho punto, podemos observar que en la parte inferior de la viga se genera estiramiento (tracción), mientras que en la parte superior se genera compresión.
Podríamos asumir que dicha viga es parte de una estructura de acero con un perfil típico en forma de “I” o doble “T”. Si realizamos un corte al perfil, observando su sección transversal, internamente podemos observar lo siguiente:
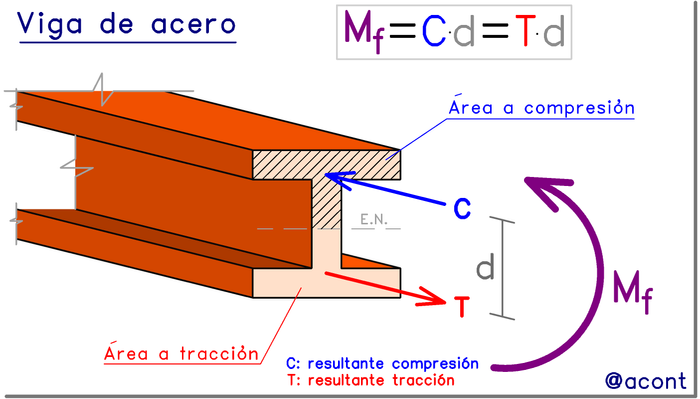
Existe un área de la sección transversal sometida a esfuerzos de compresión y otra sometida a esfuerzos de tracción. La separación entre ambas áreas es una línea recta denominada eje neutro. Ambas áreas poseen una fuerza resultante separadas a una distancia determinada “d”.
La distancia “d” entre ambas fuerzas representa el “brazo”. El momento flector es el resultado de ambas fuerzas actuando, intentando generar un giro en la sección transversal.
Debemos tener en cuenta que no siempre la tracción se presentará en la zona inferior y la zona superior se comprimirá. Esto es lo que suele suceder en el tramo central de una viga. Por otro lado, en los extremos de las vigas suele suceder lo contrario, es decir, el momento flector tiene sentido opuesto.
Convención de signos para el momento flector
Hasta ahora no he mencionado la convención de signos para esta solicitación. A diferencia de la fuerza cortante, esta convención es más fácil de visualizar. En la Fig. N°10 podemos visualizar la convención de signos.
Recordemos definir previamente los ejes locales para así saber cuál extremo es el derecho y cual el izquierdo, sobre todo en barras inclinadas.
Básicamente, el momento flector se considera positivo si tiende a generar flexión hacia abajo, es decir, si su aplicación genera una figura deformada en forma de “U”. Esto era lo que sucedía en la viga del ejemplo anterior. Si bien en Estática no se estudian las deformaciones, es una forma de visualizar efectivamente el signo de esta solicitación.
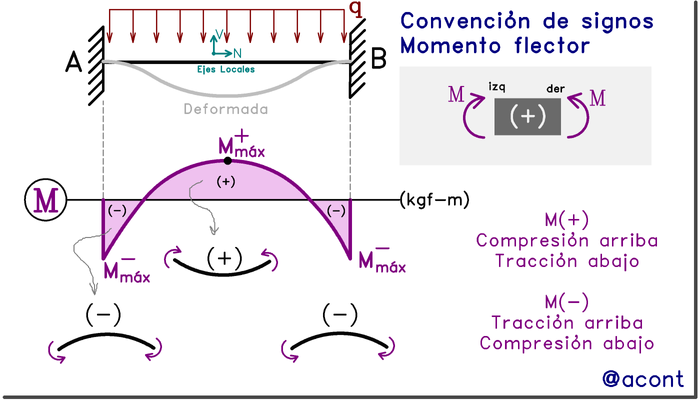
El sentido del momento es horario en el extremo izquierdo y anti horario en el extremo derecho, para el caso positivo. Tenemos una barra empotrada en ambos extremos, esto no es un sistema isostático sino hiperestático y su resolución se escapa de la Estática, pero nos sirve para representar ambos signos en el diagrama de momentos flectores.
Podemos notar que este diagrama es una imagen desplazada verticalmente del diagrama en la Fig. N°7. La presencia de restricción rotativa en los extremos de la barra genera momentos que trasladan el diagrama hacia abajo.
Aportes de esta publicación
| Se logra entender el momento flector como una solicitación cuyo efecto es el de generar flexión o curvatura en un elemento, donde existen esfuerzos internos de tracción y compresión cuyas resultantes son un par de fuerzas. Esta publicación aborda el cálculo del momento flector mediante las ecuaciones de equilibrio estático, llevando a su vez la posibilidad de graficarlo en un diagrama. Se abordaron dos de los casos de carga básicos como lo son la carga puntual y la distribuida uniforme, logrando obtener un gráfico del diagrama de momento flector en cada caso, siendo lineal y parabólico respectivamente. |
Referencias Bibliográficas
[1]Norris, C. H. y Wilbur, J. B. (1973). Análisis Elemental de Estructuras. Segunda Edición. Libros McGraw-Hill de México. (p. 97-98).Fuente
[2]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 112).Fuente
Material recomendado
•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil
•Estática Aplicada: transformación de reacciones al sistema local en barras inclinadas
•Estática Aplicada | Proyección de cargas externas al sistema local de solicitaciones
•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Cortante Parte I
•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Cortante Parte II
Imágenes de autoría propia realizadas mediante LibreCAD y Microsoft PowerPoint.
Publicado mediante la dApp STEMsocial |
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP | Registro en Hive |
Te invito también a unirte a nuestra comunidad aquí. Un grupo que se dedica a estudiar las palabras de Dios a través de las enseñanzas del hermano Eli Soriano.
¡Pregúntele al hermano Eli, la Biblia responderá!Consulte el siguiente enlace👇👇👇
https://peakd.com/c/hive-182074/created
Muchas gracias por visitar y valorar el contenido. Gracias también por la invitación.
Congratulations @acont! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Thanks for the info! 👍
You are very welcome @acont 👍🙂
Support us back and vote for our witness.
You will get one more badge and more powerful upvotes from us on your posts with your next notifications.
#POSH
Compartido en Twitter:
https://twitter.com/AngelCont96/status/1290775822295605248?s=20
Excelente artículo amigo @acont. Interesante la diferencia que haces entre momento y momento flector, esfuerzo representativo de un elemento estructural sometido a flexión pura, como lo son las vigas. A partir del conocimiento de la sección transversal de una viga de concreto armado (disposición del acero inferior, acero superior, f'c del concreto) podemos desarrollar diagramas momento-curvatura para evaluar la sección; donde tener estos conceptos claros es muy importante.
Excelente la explicación didáctica que haces de la flexión, donde para un sentido de momento en particular, unas fibras van a traccionarse y otras van a comprimirse.
Felicidades @acont, éxitos y bendiciones!
Aunque no tiene mucha importancia, quería dejar claro la diferencia, porque en realidad no es lo mismo un momento cualquiera que un momento flector.
Ese es un diagrama que debo repasar un poco, aunque creo que tienes material sobre eso en tu blog, más que todo lo he manejado en estructuras de acero. Así se comprueba la ductilidad de la viga.
Gracias por visitar @eliaschess333 éxitos para ti también!
Muchas gracias @mayvileros por el apoyo a mi blog 👍. Un saludo!
Siempre a su orden 😉 saludos.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support. Using the STEMsocial app could yield even more supporti next time.
Thanks! 👍💪
Mu importante el concepto de momento tanto para las condiciones estáticas y dinámicas que se dan dentro de la ingeniería, en el caso de la ingeniería de petróleo para nosotros es de mucho interés el cálculo de momento, pero para el caso de nosotros el tipo de momento que calculamos lo determinamos torque y lo medimos en el sistema de medidas inglesas en lbsf x pie. Incluso cuando la tubería de perforación se llego a pegar en el fondo del hoyo, teníamos que estar muy pendiente para darle el valor exacto en lbf-pie a los perforadores porque muchos perforadores miraban la aguja que esta mide en el sistema internacional en N-m y terminaban metiendole un torque mayor a la tubería hasta que la partían, y luego bueno a aguantar la pela en los regaños por la mala acción.
Saludos mi estimado amigo por compartir estos post muy importantes no solo en la ingeniería civil sino en la ingeniería en general.
Muy interesante lo que comentas, en este caso sería el momento dinámico o torque en un perforación petrolera. Me imagino la complicación de medirlo en otras unidades, ya que conlleva doble conversión. Muy importante el momento en muchas aplicaciones de la ingeniería. Saludos compañero.
Muy buen contenido amigo @acont. Siempre resulta interesante leer tus artículos aunque no es mi área. Muy buen explicación de la flexión, en ingeniería son múltiples las aplicaciones que tiene el concepto momento, y en el caso de los elementos estructurales me imagino la importancia que tiene. Saludos!
Efectivamente tiene muchas aplicaciones importantes estimado @emiliomoron, tal como comentaba el amigo carlos84. Gracias por pasar, saludos!