Equilibrio de estructuras con cargas perpendiculares al plano — Parte IV (Despiece)
En las estructuras con cargas perpendiculares al plano, se puede realizar un estudio del equilibrio interno a través del cálculo de las reacciones que existen internamente, las cuales se transmiten de un elemento a otro por equilibrio de fuerzas.
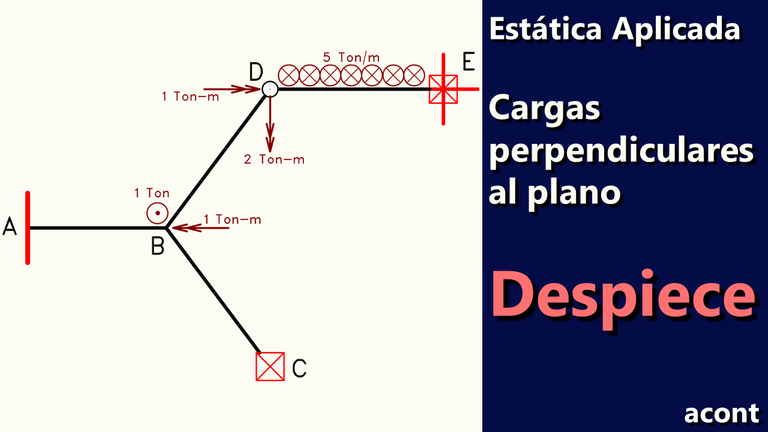
Anteriormente, abordamos aspectos generales de las estructuras con cargas perpendiculares al plano y el cálculo de reacciones externas en las siguientes publicaciones:
•Equilibrio de estructuras con cargas perpendiculares al plano — Parte I (Introducción)
En esta ocasión, se abordará la realización del despiece del siguiente sistema isostático, enfocándonos en el cálculo de reacciones externas, siendo las reacciones externas incógnitas ya conocidas como condición inicial, para así no alargar esta publicación.
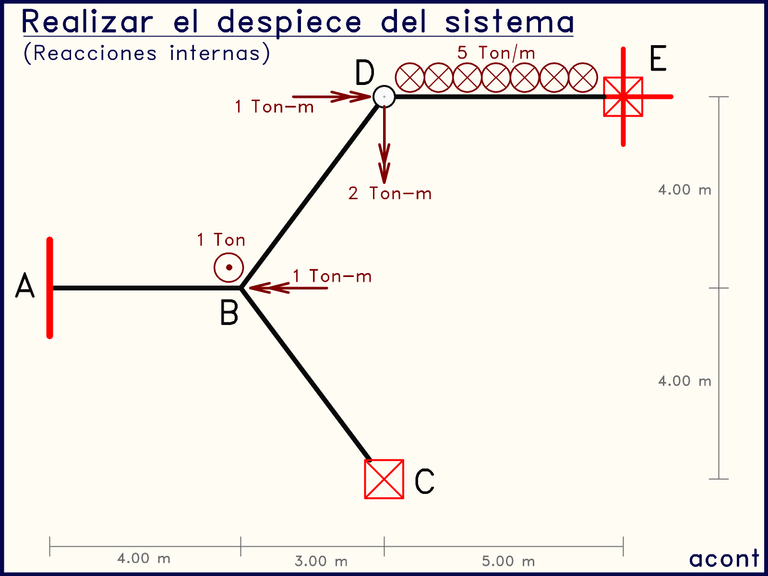
Para el cálculo de las reacciones externas (en caso de que se quiera practicar esto) puedo recomendar la siguiente serie de pasos, tomando en cuenta siempre que primero es recomendable plantear una serie de pasos, y una vez establecido el camino, realizar el cálculo numérico:
ΣMDX=0. Sumatoria de momento en "X" sobre rótula "D" (subsistema "ABCD"). Se calcula CZ.
ΣMDY=0. Sumatoria de momento en "Y" sobre rótula "D" (subsistema "ABCD"). Se calcula MAY.
ΣFZ=0. Sumatoria de fuerzas en "Z" sobre todo el sistema. Se calcula EZ.
ΣMDX=0. Sumatoria de momento en "X" sobre rótula "D" (subsistema "DE"). Se calcula MEX.
ΣMDY=0. Sumatoria de momento en "Y" sobre rótula "D" (subsistema "DE"). Se calcula MEY.
Este es un posible camino a seguir para el cálculo de las reacciones externas. Se debe recordar que los momentos sobre la rótula se deben colocal hacia el subsistema más rígido (consultar partes anteriores).
Los resultados de las reacciones se reflejan en la siguiente imagen:
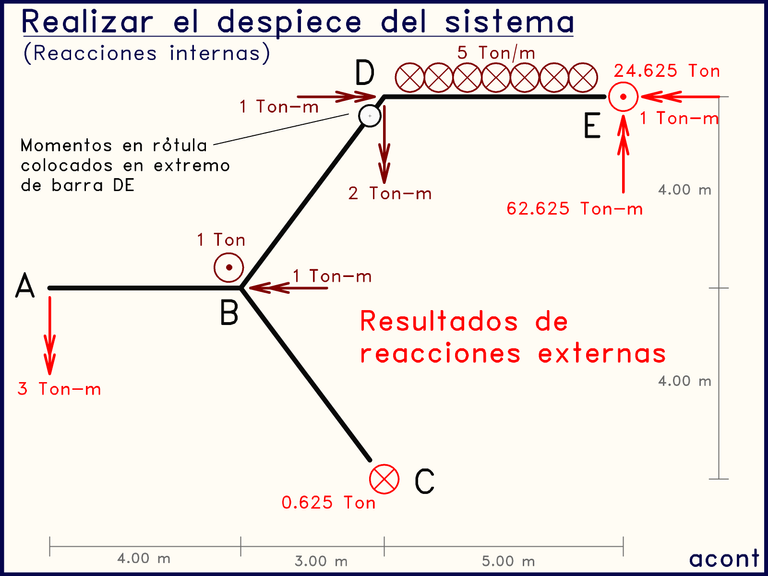
Conocidas las reacciones externas, podemos proceder con el despiece o cálculo de las internas. Para ello, debemos empezar por algún extremo del sistema.
-Escogeremos empezar por la barra "AB". Lo que debemos realizar es calcular mediante las tres ecuaciones básicas de equilibrio estático, las reacciones internas en el extremo "B" (en azul) que le dan equilibrio a la barra por si sola, siendo ya conocida la reacción externa de "A" (en rojo).
Debemos tener en cuenta si en el sistema el punto "B" representa una junta rígida o si representa una rótula. Si se trata de una rótula, los momentos en el extremo de la barra deben ser nulos, de lo contrario serán generalmente diferentes de cero.
-Ya que el punto "B" es una junta triple que une a tres "ramas", debemos escoger otra "rama" y llegar a al punto "B" a través de esta otra rama.
-Por lo anterior, procedemos ahora a a calcular las reacciones internas del extremo "B" de la barra "BC" (en azul), siendo ya conocida la reacción externa de "C" (en rojo).
Hemos obtenido dos grupos de fuerzas en el extremo "B" de ambas barras, las cuales se transmiten en sentido contrario a la junta "B" (dibujada a parte).
Todo lo anterior se observa en la siguiente imagen animada:
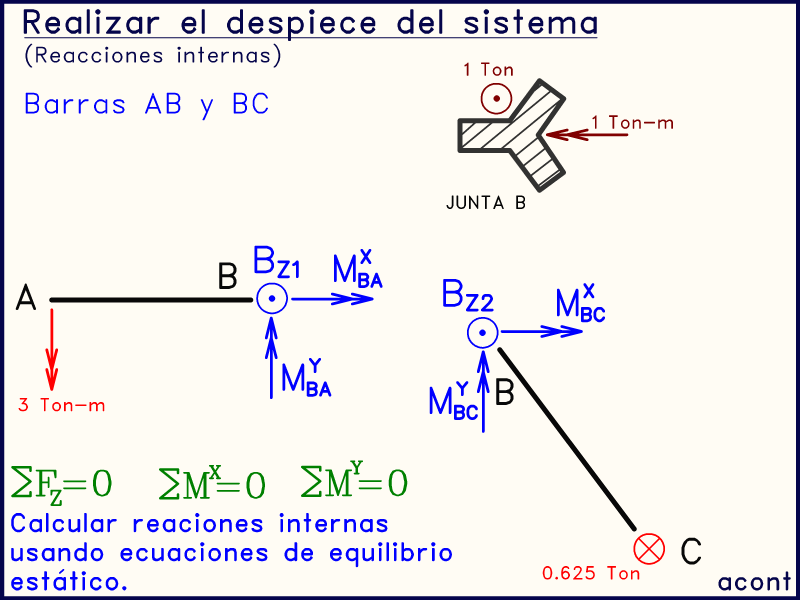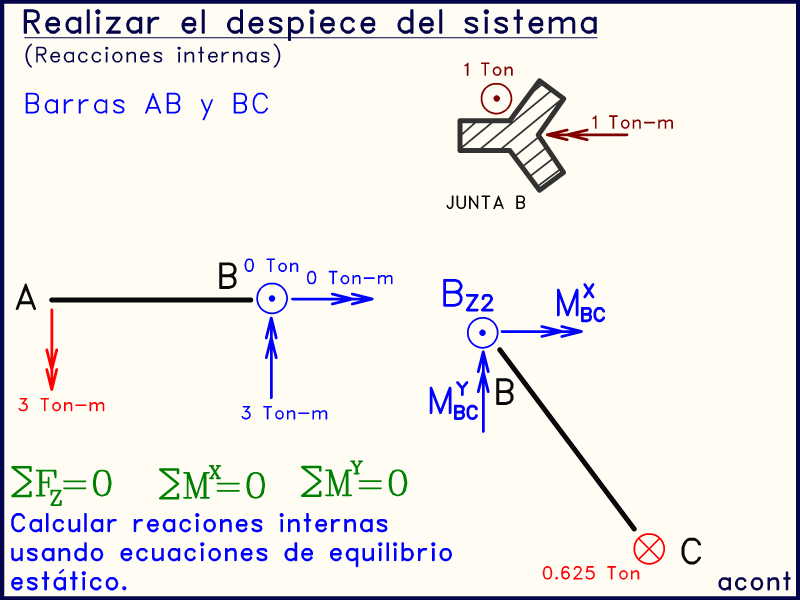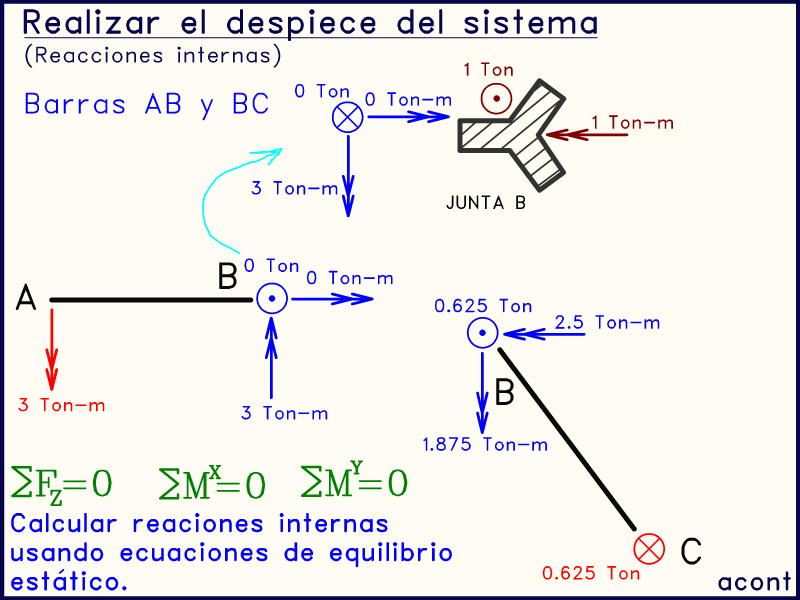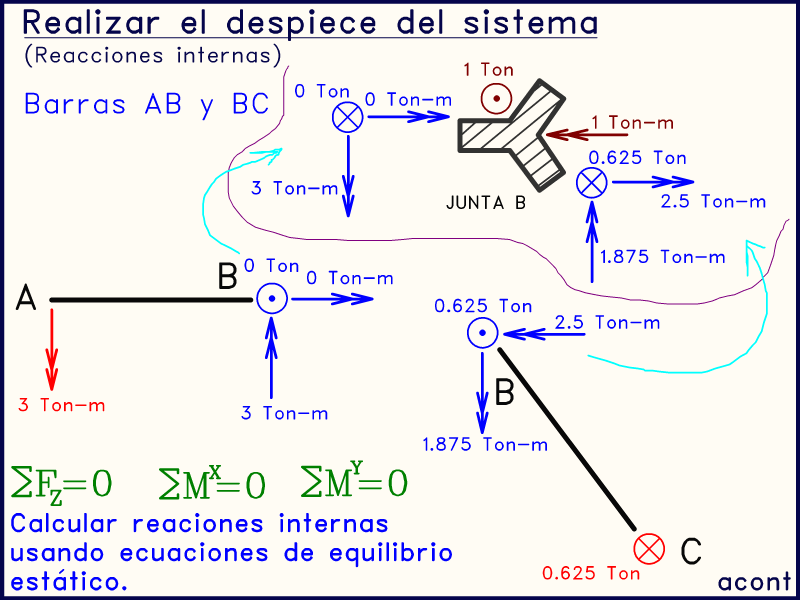
Las cargas externas que se aplican puntualmente en la junta rígida "B" se deben dibujar sobre la misma junta, y no en el extremo de alguna de las barras, para así estudiar a parte el equilibrio de la junta.
La junta "B" une a tres barras, y conocemos ya 2 grupos de fuerzas provenientes de dos de estas barras. Debemos calcular el tercer grupo de fuerzas, el cual se transmitirá a la barra "BD".
Para ello, utilizamos las tres ecuaciones de equilibrio para calcular las fuerzas necesarias para garantizar el equilibrio de la junta:
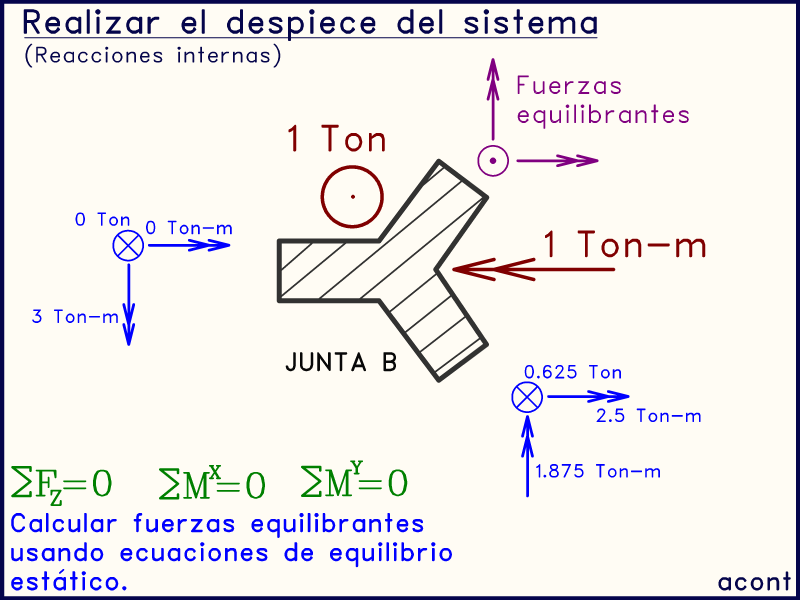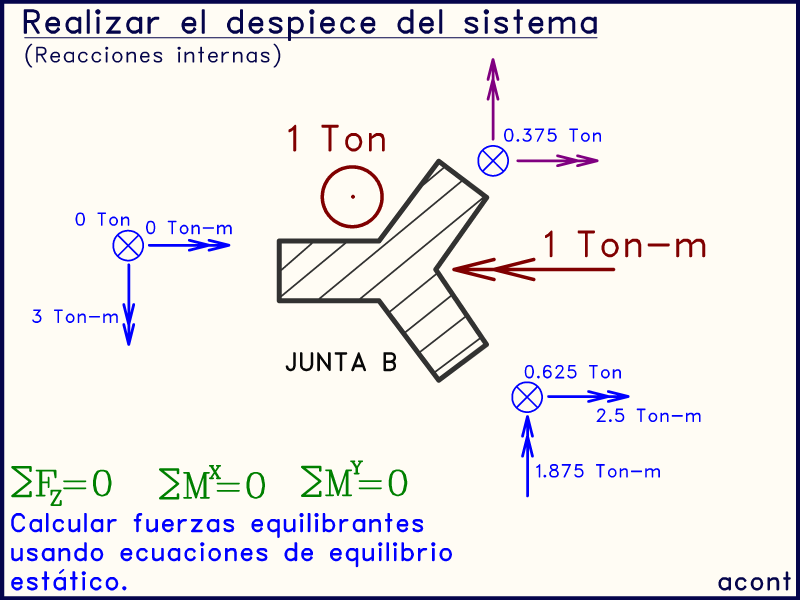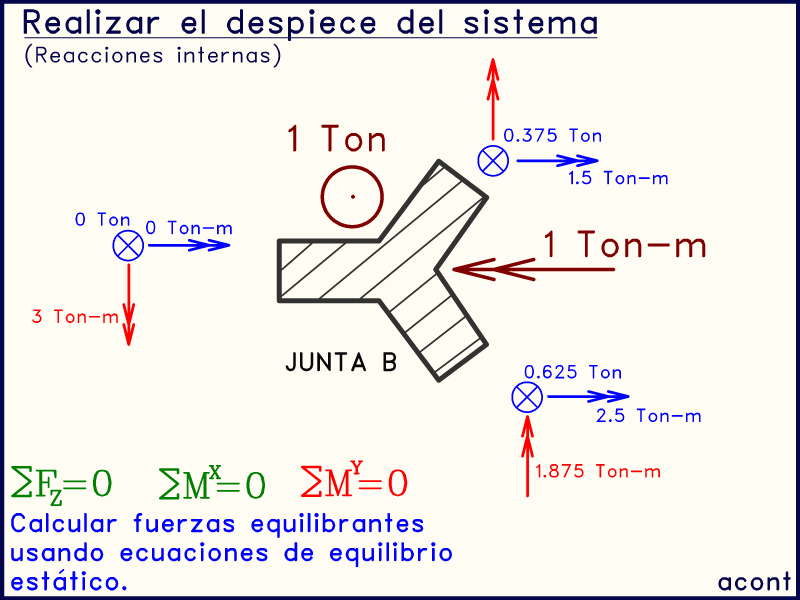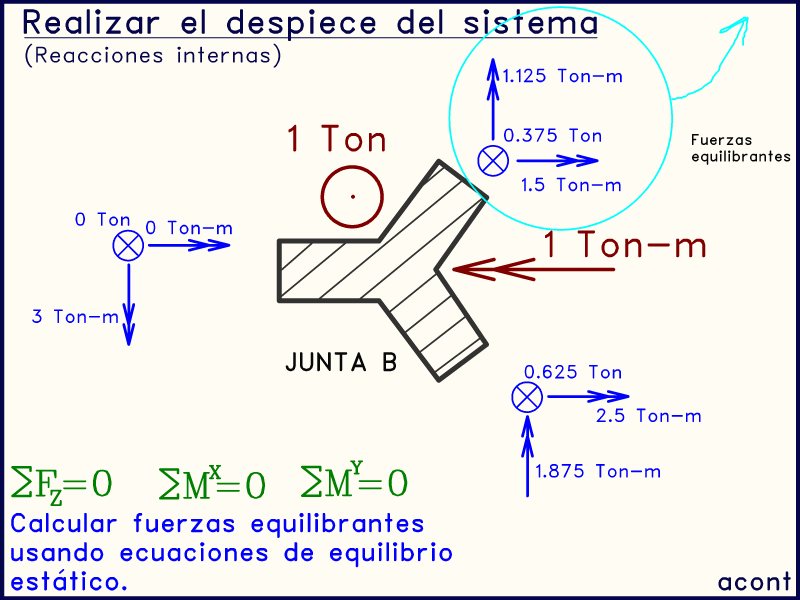
Este último grupo de fuerzas sobre la junta, las que hacen falta para alcanzar el equilibrio de fuerzas y momentos en ella, son llamadas "fuerzas equilibrantes", y son nuestro tercer grupo de fuerzas, las cuales se transmiten a la siguiente barra ("BD").
En la imagen animada anterior, se muestra en rojo las fuerzas o momentos que estamos sumando para calcular las fuerzas equilibrantes.
En la siguiente imagen animada, se muestran las últimas dos barras ("BD" y "DE"). Las fuerzas equilibrantes de la triple junta "B" se transmiten en sentido contrario a la barra "BD".
Posteriormente, se calculan las reacciones internas en el extremo "D" de la barra "BD". Utilizando las ecuaciones de equilibrio estático, llegamos a que los momentos en el extremo "D" son nulos. Esto debe ser así ya que en la imagen original del sistema allí se encuentra una rótula:
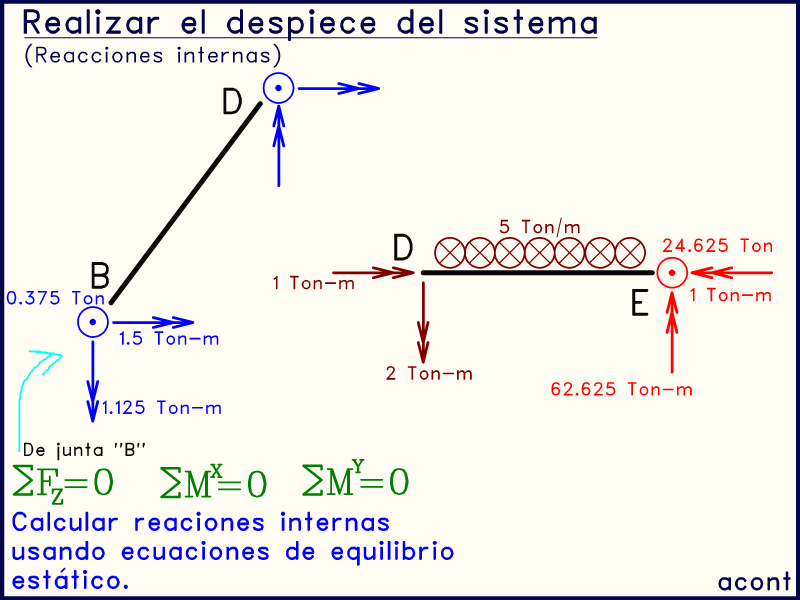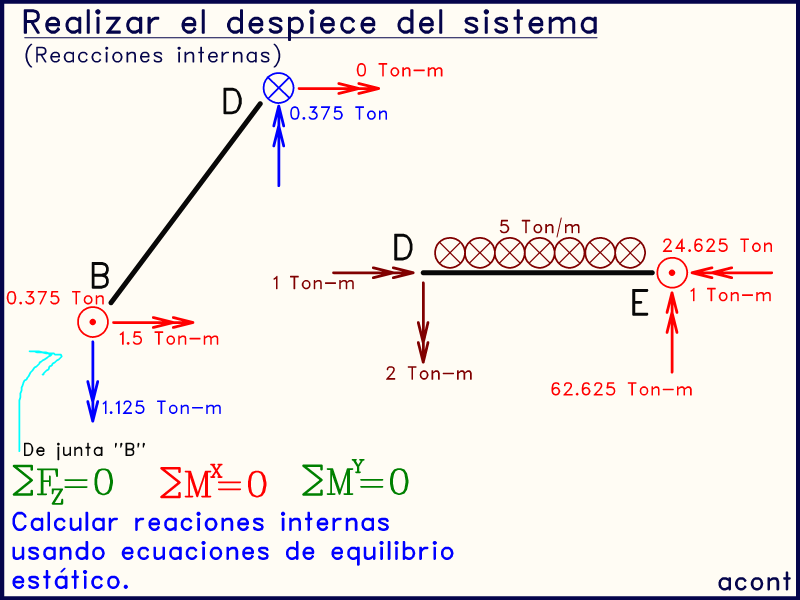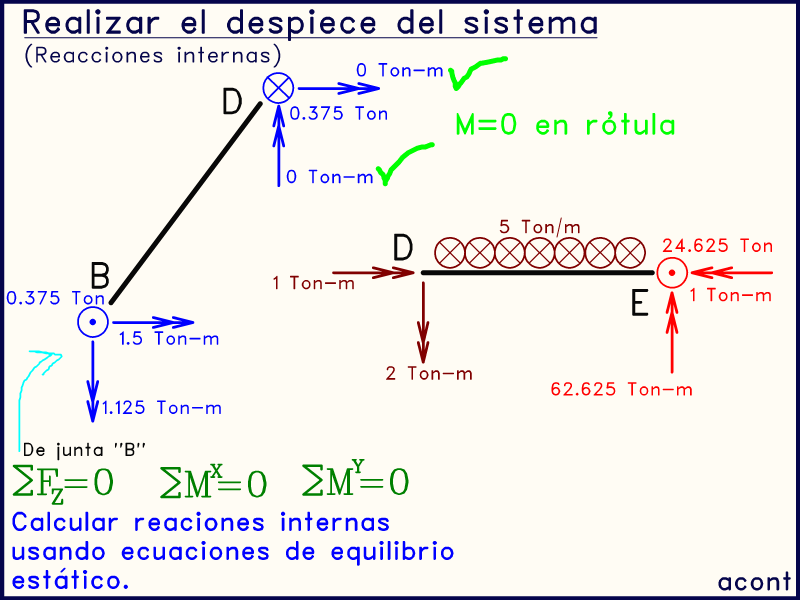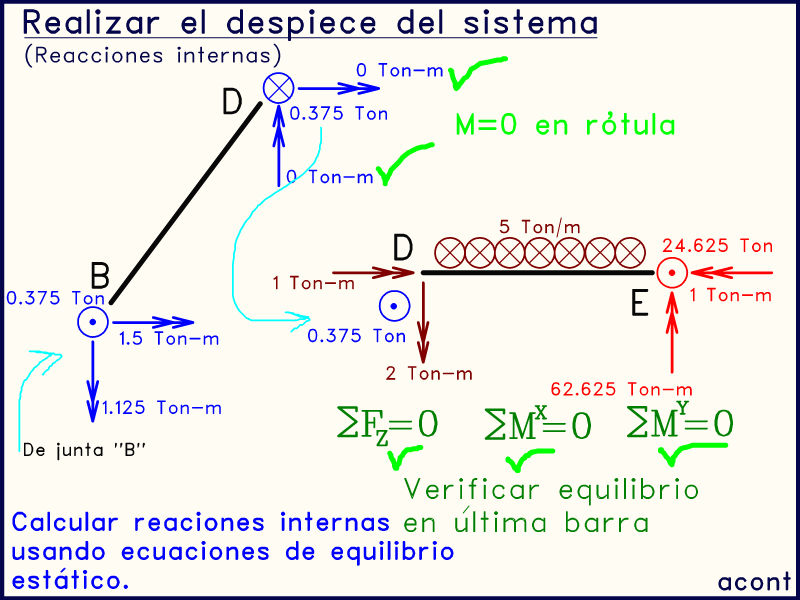
Debemos tener siempre presente que vínculos internos existen en el sistema original, para comprobar que las reacciones internas concuerden con estas condiciones de vinculación. En este caso, la rótula indica que los momentos internos en "D" (azul) deben ser nulos.
Por último, transmitimos la fuerza puntual interna de 0.375 Ton en sentido contrario al extremo de la barra "DE". En esta última barra, en su extremo, deben aparecer los momentos externos (rojo oscuro) que hemos decidido colocar allí en la parte inicial del problema.
En esta última barra, al no existir más incógnitas internas (ya se conocen las reacciones externas en "E"), se debe verificar que existe equilibrio estático a través de las ecuaciones de equilibrio. Si no se cumple, se debe revisar cálculos previos. De esta manera, se ha realizado el estudio del equilibrio interno del sistema, a través de las reacciones internas que se transmiten de barra a barra.
En las siguientes publicaciones se dará paso a diagramas de solicitaciones de estructuras con cargas perpendiculares al plano. Esto incluye solicitaciones como fuerza cortante en "Z", momento flector y momento torsor, esta última siendo una solicitación que no habíamos abordado previamente.
Aportes de esta publicación
Esta publicación brinda material explicativo respecto al despiece y cálculo de reacciones internas en sistemas con cargas perpendiculares al plano. Representa un aporte al material disponible en la web sobre el tema, ya que es poco abordado en las fuentes disponibles, siendo útil para estudiantes que necesiten estudiar el tema a mayor profundidad.
Referencias
•Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 202-204, 221-223).Fuente
Imágenes de autoría propia realizadas mediante LibreCAD y PowerPoint. GIFs elaborados mediante Photoscape.
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| ¡Gracias por visitar! — ¡Thanks for visiting!  |
Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a usar nuestra etiqueta ENLACE y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
¿QUIERES AUTOMATIZAR TUS GANANCIAS DE CURACIÓN? SE PARTE DEL PROYECTO ENLACE APOYANDO A NUESTRO TRAIL EN HIVE.VOTE INGRESA AQUÍ PARA CONCOCER LOS DETALLES.
¿QUIERES INVERTIR ENLACE? DESCUBRE COMO HACERLO Y GENERAR INGRESOS DE FORMA SEMANAL MEDIANTE TU DELEGACIÓN DE HP AQUÍ TE EXPLICAMOS COMO.
Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS
Atentamente
EQUIPO ENLACE 2021
Gracias por el apoyo del equipo Enlace!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
https://twitter.com/EspanolStem/status/1371986690961772550