Equilibrio de estructuras con cargas perpendiculares al plano — Parte II
Esta publicación aborda el cálculo de reacciones externas en sistemas isostáticos en el plano X-Y, con cargas perpendiculares a él. Viene como complemente a la anterior publicación en donde se aborda aspectos generales teóricos.
Anteriormente, se realizaron las siguiente publicaciones relacionadas a este tema:
•Introducción a las estructuras con cargas perpendiculares al plano | Estática Aplicada
•Equilibrio de estructuras con cargas perpendiculares al plano | Estática Aplicada
En la presente entrega, se abordará de manera práctica la resolución de un sistema con cargas perpendiculares al plano. Es común entre los estudiantes que sea difícil dominar el abordaje de estos sistemas, ya que se debe pensar en una proyección distinta a la usual, donde las cargas están en el plano.
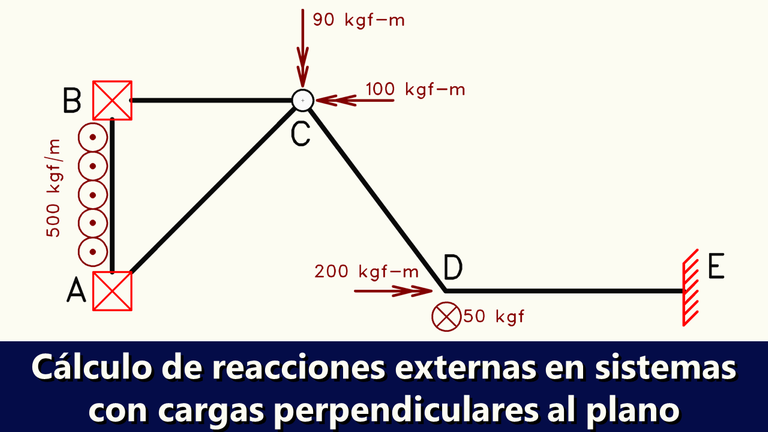
El sistema a resolver es el siguiente:
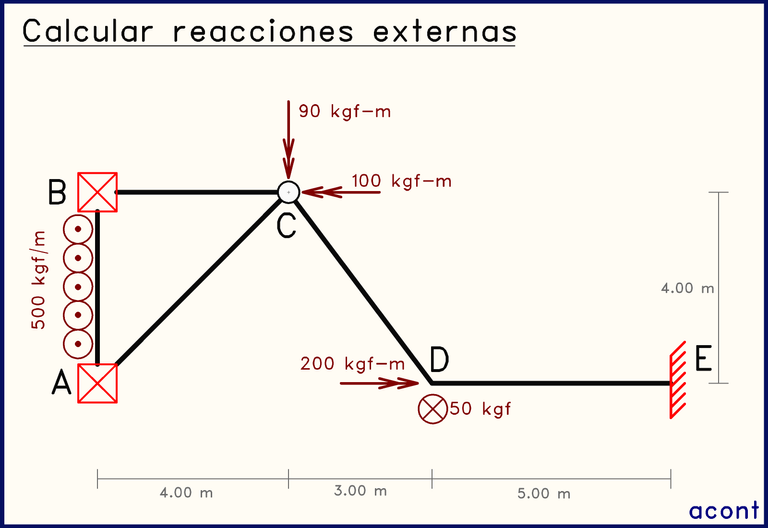
Podemos observar que el sistema posee las siguientes vinculaciones externas: apoyos simples en "A" y "B", y un empotramiento en "E". Esta representación del empotramiento es la misma que se había usado en temas anteriores a este, y es equivalente a la respresentación dada en esta publicación previa (Introducción al tema), por lo que se pueden usar indistintamente.
Tenemos distintas cargas externas, compuestas por 3 momentos, 2 aplicados sobre la rótula "C" y uno sobre la junta rígida "D". Existe una fuerza puntual de 50 Kgf orientada en sentido negativo en "D" y una carga distribuida en sentido negativo de 500 Kgf/m aplicada sobre la barra AB. Ya abordamos la convención de signos para estas cargas en la introducción a este tema.
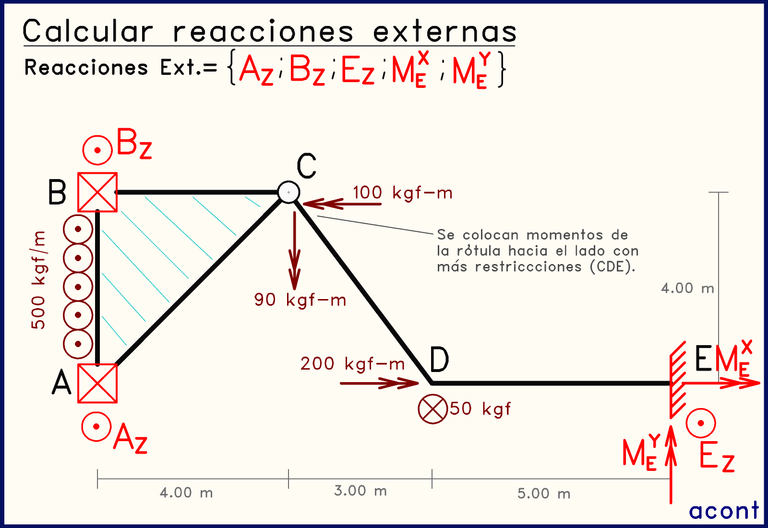
En la publicación anterior, donde damos inicio al estudio del equilibrio de estos sistemas, se habló del caso de momentos aplicados en rótulas, algo particular de este tema. Es por esta razón, que los momentos aplicados en la rótula se asumirán estar aplicados sobre el extremo "C" de la barra "CD", ya que el subsistema "CDE" presenta mayor cantidad de restricciones (reacciones en "D").
Otro aspecto a tomar en cuenta, es que la triangulación "ABC" puede tomarse como un solo cuerpo rígido o chapa. Es decir, se puede decir que el sistema está compuesto por 2 chapas.
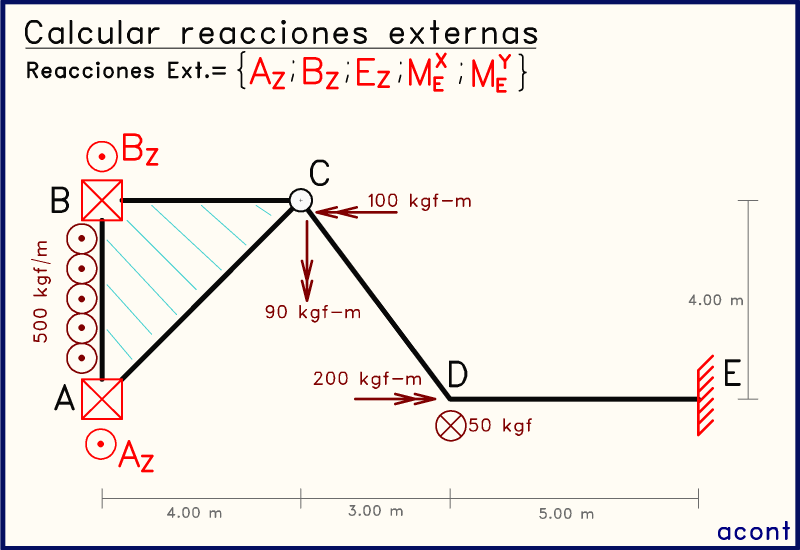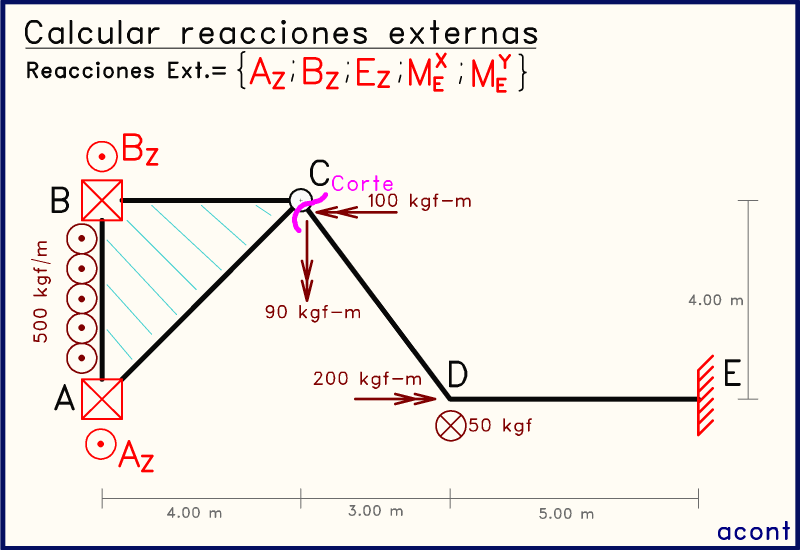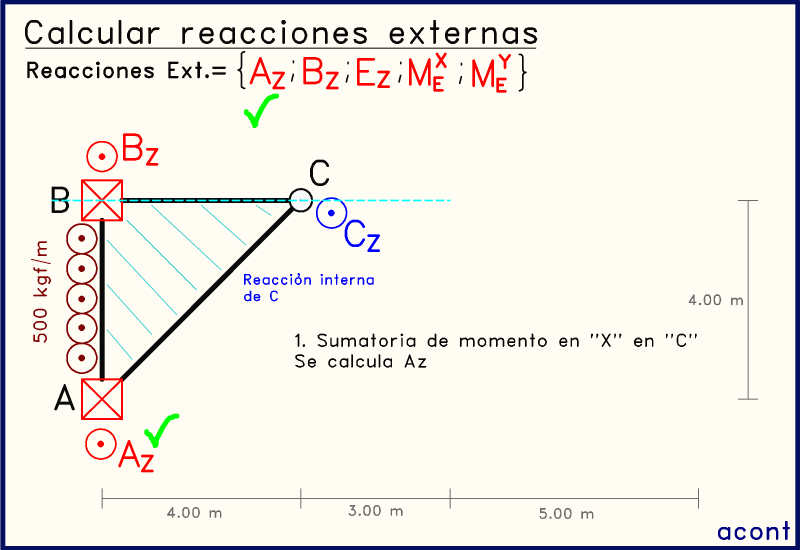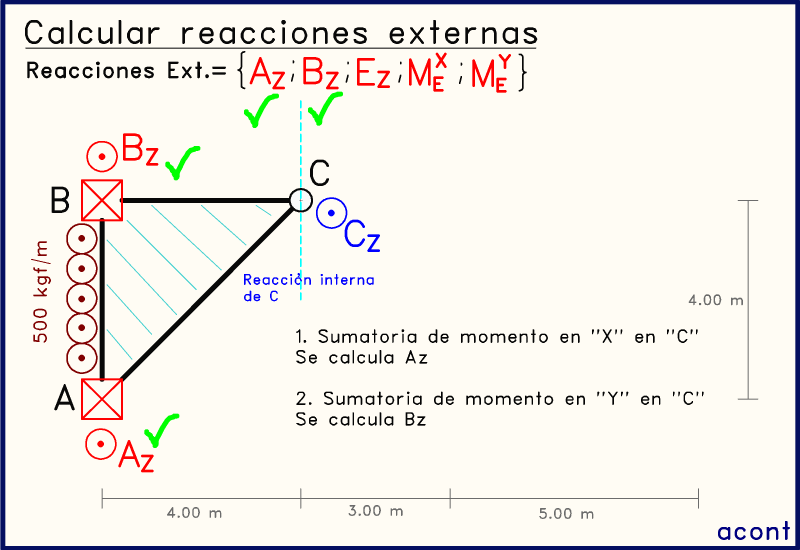
Los apoyos simples presentan dos restricciones puntuales (incógnitas de fuerza AZ y BZ). Mientras que el empotramiento brinda todas las restricciones al impedir todo movimiento (EZ, MEX y MEY).
Como ya sabemos, las rótulas nos brindan la posibilidad de realizar un corte y separar el sistema en subsistemas. Es por este motivo que en la animación anterior se realiza un corte y nos quedamos con el subsistema de la izquierda (ABC), ya que este presenta menor cantidad de incógnitas. Lo ideal es buscar siempre despejar una incógnita con una sola ecuación y a mayor cantidad de incógnitas esto se dificulta o se hace imposible.
Producto del corte va a aparecer una reacción interna de fuerza en la rótula (CZ), la cual no nos interesa ya que solo estamos calculando las reacciones externas.
Para utilizar las ecuaciones de equilibrio estático con efectividad, debemos observar la geometría del sistema tratando de buscar maneras de anular algunas incógnitas presentes.
Al realizar una sumatoria de momentos alrededor del eje "X" en el punto "C", se ve que la fuerza BZ no posee brazo de momento, y la reacción interna de la rótula tampoco. Esto nos da la posibilidad de obtener una ecuación que solo contiene a AZ:
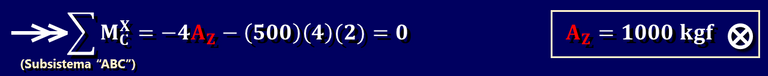
Al hacer esto, teóricamente estamos utilizando una ecuación de condición (dada por la rótula), sin embargo, no nos preocuparemos por el entramado teórico de esto sino por tener siempre en mente la utilidad de las rótulas.
Seguidamente, podemos realizar una sumatoria de momentos alrededor del eje "Y" en el punto "C", para así anular la incógnita interna de "C" y poder calcular BZ:
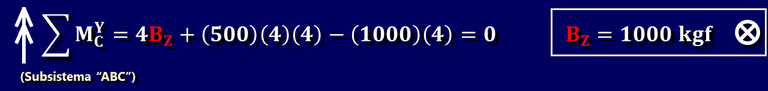
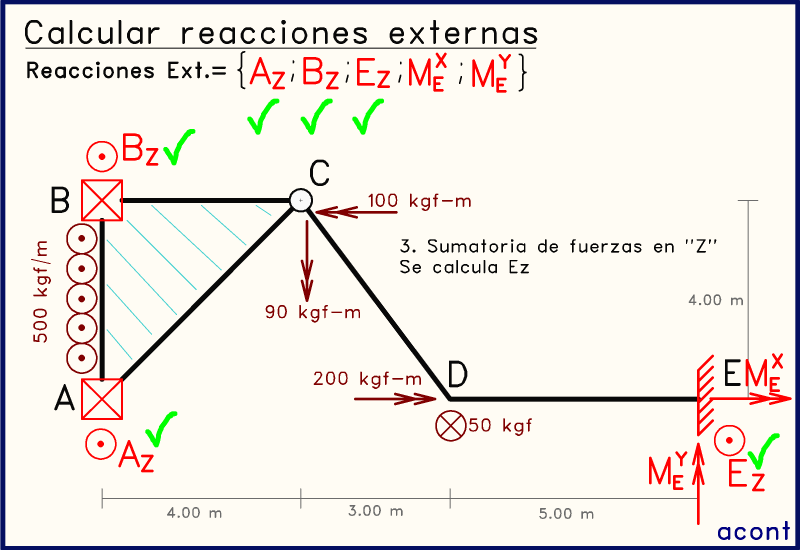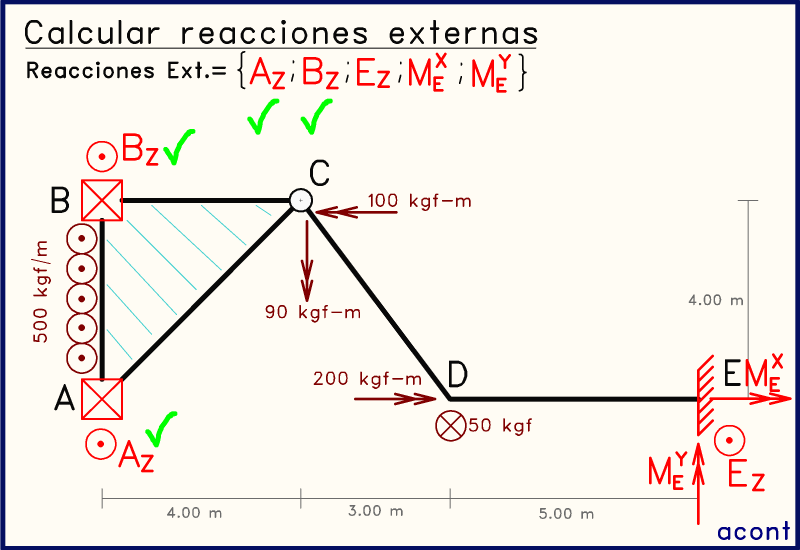
Observando la animación, tenemos solo tres fuerzas incógnitas en dirección del eje "Z", de las cuales ya conocemos dos. Por esta razón, mediante una simple sumatoria de fuerzas en dirección del eje "Z", tendremos una ecuación que solo tiene una incógnita: EZ.

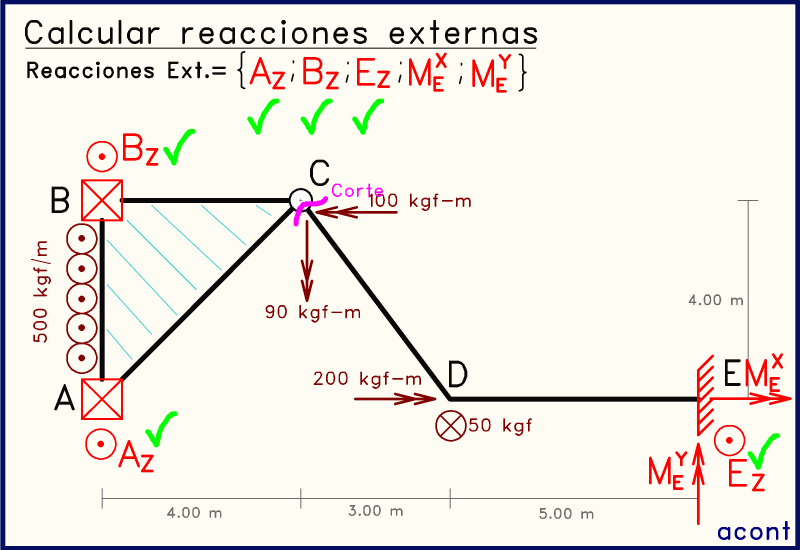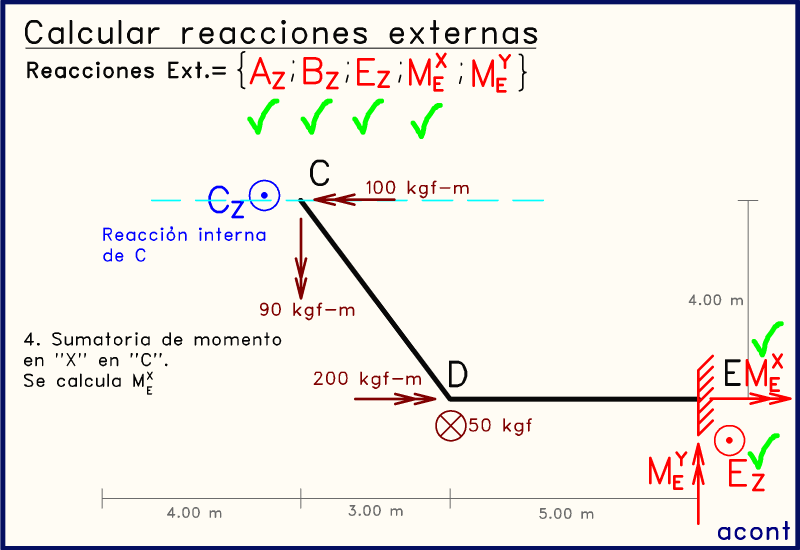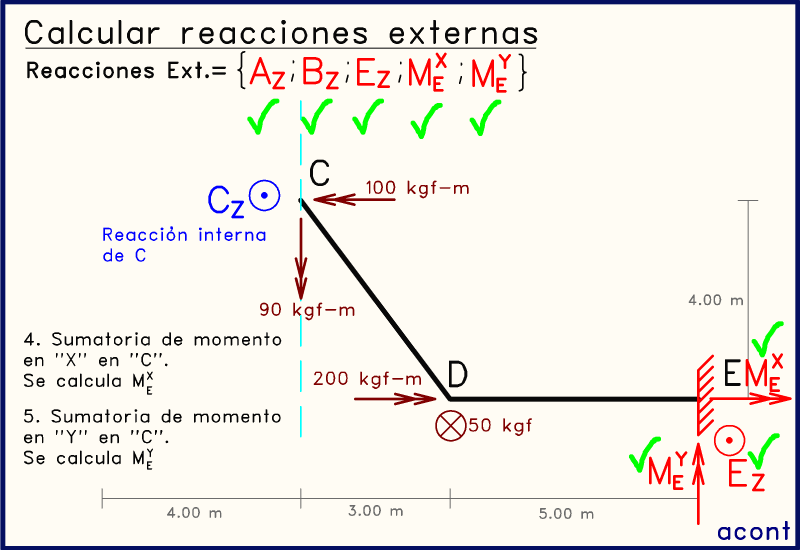
Ahora nos enfocaremos en el subsistema de la derecha. Va a suceder lo mismo que en el subsistema anterior. Al realizar una sumatoria de momentos, ya sea en el eje "X" o en el eje "Y", tendremos una sola incógnita en ambos casos, ya que EZ ya es conocido.
Podemos plantear entonces una sumatoria de momentos alrededor del eje "X" en cualquier punto para así obtener una ecuación que solo contiene a MEX:
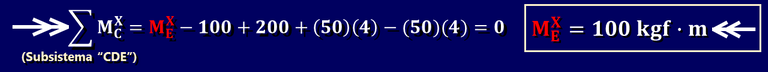
Ahora, solo nos queda plantear una sumatoria de momentos alrededor del eje "Y" en cualquier punto para hallar MEY:
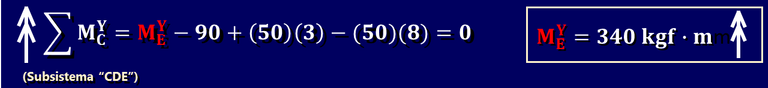
De esta manera, ya hemos hallado todas las reacciones o incógnitas externas. En próximas publicaciones abordaré casos más complejos en el cálculo de reacciones así como despieces (cálculo de reacciones internas) del sistema.
Aportes de esta publicación
Se brinda un enfoque más profundo en la resolución de estos sistemas, abordando en detalle el análisis previo a la aplicación de las ecuaciones de equilibrio, para así aplicar estas de la manera más efectiva posible. La clave para resolver estos ejercicios es dominar el análisis previo de la geometría del sistema y de como podemos aprovechar las rótulas (ecuaciones de condición) para calcular las primeras incógnitas.
Referencias
•Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 202-204, 214).Fuente
Imágenes de autoría propia realizadas mediante LibreCAD y PowerPoint. GIFs elaborados mediante Photoscape.
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| ¡Gracias por visitar! — ¡Thanks for visiting!  |
Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a usar nuestra etiqueta ENLACE y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
¿QUIERES AUTOMATIZAR TUS GANANCIAS DE CURACIÓN? SE PARTE DEL PROYECTO ENLACE APOYANDO A NUESTRO TRAIL EN HIVE.VOTE INGRESA AQUÍ PARA CONCOCER LOS DETALLES.
¿QUIERES INVERTIR ENLACE? DESCUBRE COMO HACERLO Y GENERAR INGRESOS DE FORMA SEMANAL MEDIANTE TU DELEGACIÓN DE HP AQUÍ TE EXPLICAMOS COMO.
Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS
Atentamente
EQUIPO ENLACE 2021
Gracias al equipo de #Enlace.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support. Using the STEMsocial app could yield even more supporti next time.
Thanks for the support!
Your post has been voted as a part of Encouragement program. Keep up the good work!
Try https://ecency.com and Earn Points in every action (being online, posting, commenting, reblog, vote and more).
Boost your earnings, double reward, double fun! 😉
Support Ecency, in our mission:
Ecency: https://ecency.com/proposals/141
Hivesigner: Vote for Proposal
Thank you @ecency I will give a try to Ecency.com
https://twitter.com/EspanolStem/status/1360417160561127425