Greetings fellow Hive community, welcome back to my blog, where you can find content from the broad universe of science, mathematics, biology, physics, chemistry, philosophy and general knowledge accompanied by scientific outreach, a special hello to the communities Spanish-speaking communities that stimulate science content.

Introduction

Continuing in the moment of inertia dynamics, where in a previous publication I addressed the following, a moment of rotation is referred to, where this implies both the force carried out and the distance to the point of rotation, which links both, to now well friend reader the most unique of all this take into account in a simple way to have reference about dynamic moment, for this opportunity at the moment of inertia in parallel axis, where moment of inertia of any object on an axis through of its center of mass is the minimum moment of inertia on an axis in that direction of space. The moment of inertia on an axis parallel to that axis that passes through the center of mass is given by:

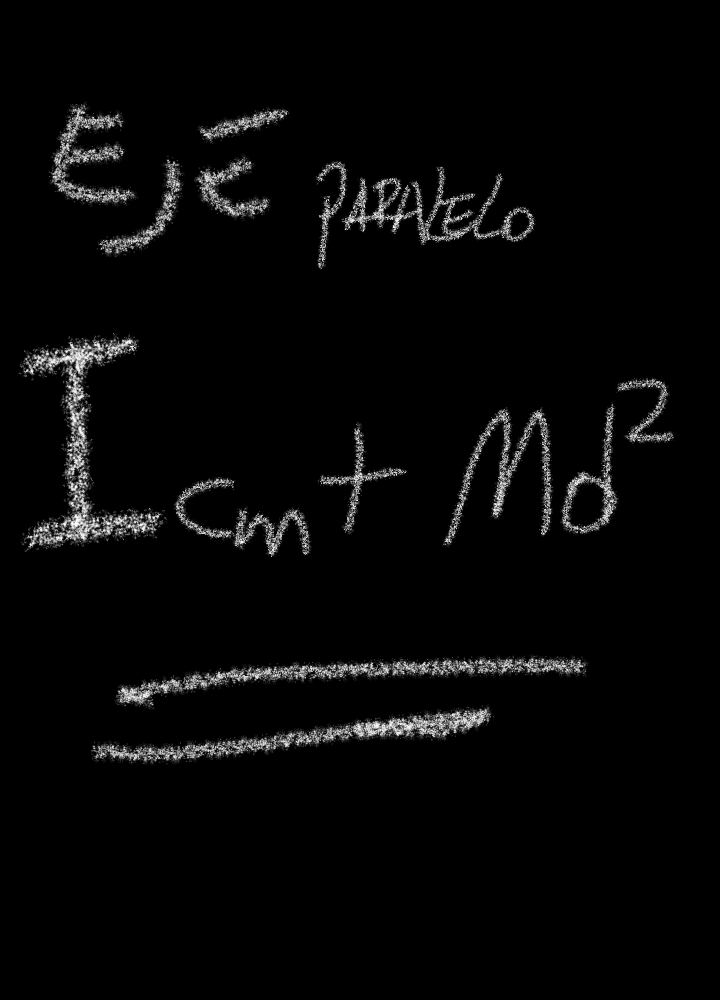
Thanks to this equation it allows us to differentiate the indirect calculation of moment of inertia thanks to that moment of inertia around a parallel axis, this is defined by is the sum of the moment of inertia of the object on its center of mass, more the moment of inertia of the entire object or body, as a point mass at the center of mass on that parallel axis.

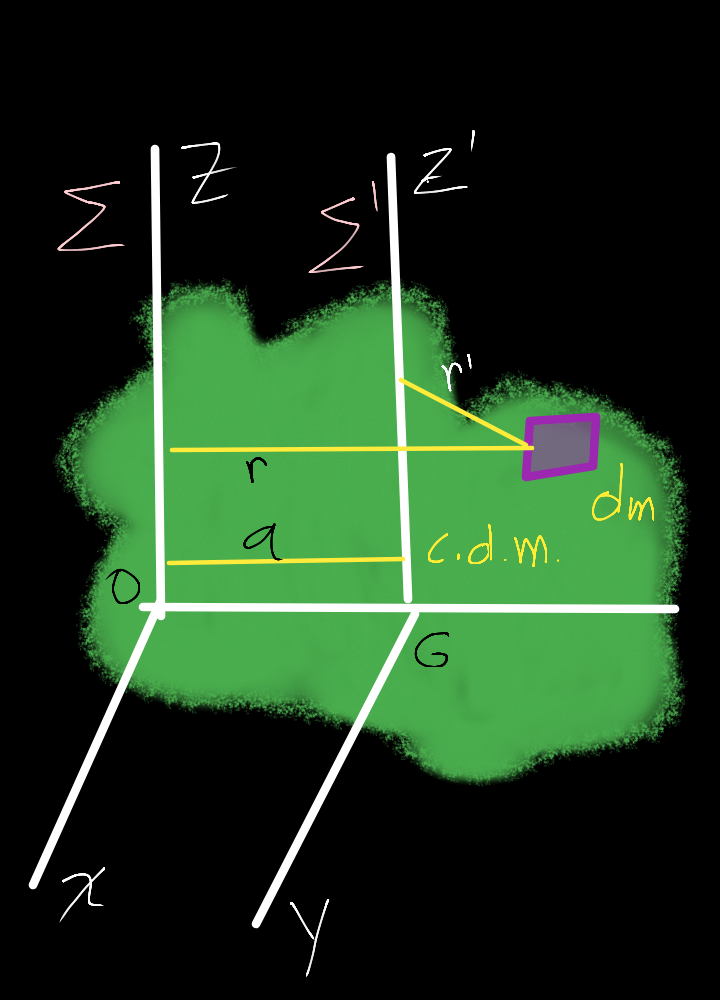
Thanks to the graph it shows us as: Io the moment of inertia with respect to an axis in Z ', which passes through the center of mass G, if "a" is the separation between both axes.

For a case like this, Steiner's Parallel Axis Theorem is usually used, where the moment of inertia around a parallel axis is considered, defined by the sum of the moment of inertia of the object, flat body or having characteristics of flat bodies of geometric shape, on its center of mass, through the same intersection between the object and its perpendicular plane.

Starting from the theorem's approach, the Cartesian coordinate system establishes, where the distance along is perpendicular between x, y; since the center of mass is at the origin.

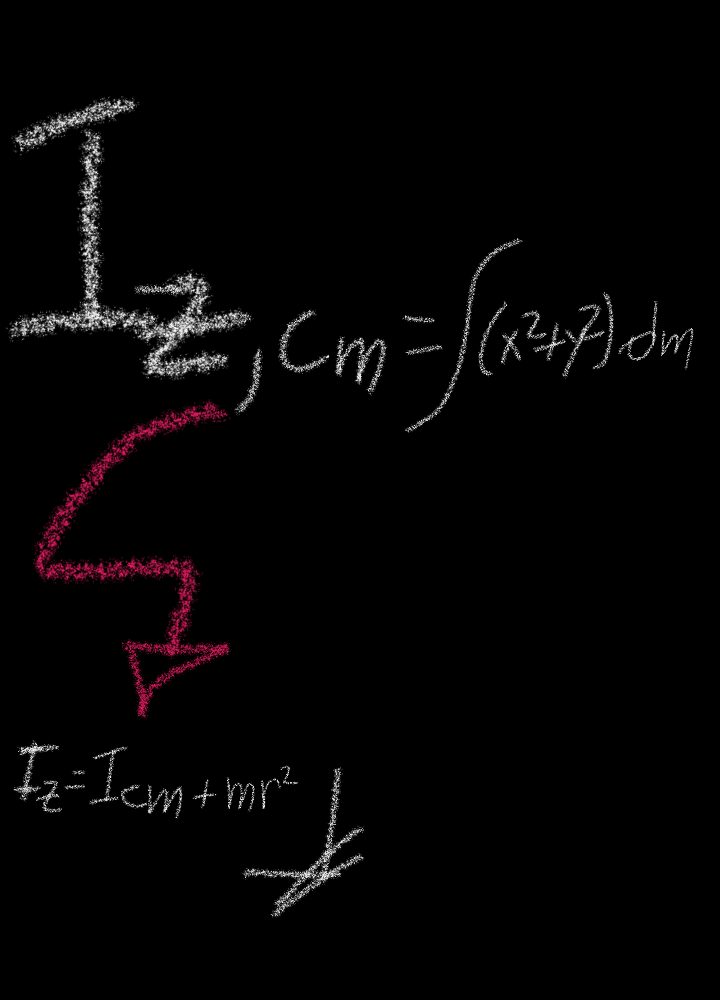
Depending on the location of the axes, the dm coordinates must be met:

x = x ', y = y' + a, z = z 'where:

r '^ 2 = x'^ 2 + y

r ^ 2 = ×^ 2 + y^ 2

In the case of Z, the moment of inertia Io:

Io= ∫r^2.dm= ∫(x^2+y^2).dm=

∫(x'^2 + y'^2 +2 .a.y'a^2).dm=

∫(x'^2 + y'^2).dm + 2.a.∫y'.dm+a^2.∫dm

∫(x'^2 + y'^2).dm.

[1]-Physics for science and technology. I by Paul Allen Tipler, Gene Mosca, 2004.