Understanding Big O Notation

Algorithms are specific sets of tasks a computer performs to solve a problem. An algorithm can be as simple as adding two numbers together, or as complex as calculating a rocket’s trajectory.
Be it complex or simple, one major factor that is always considered when choosing an algorithm to use for any operation is the efficiency. The efficiency of an algorithm is determined by how fast the algorithm can perform a given task.
When measuring how fast an algorithm is, we do not take real time into account. Rather, what is considered is the amount of “steps” that will be required by the algorithm to complete its task in a worst-case scenario.
The reason why this is done is due to the difference in the hardware capabilities of computers. Some computers are better than others in terms of speed and processing. What this means is that a computer X equipped with an 8GB RAM chip for example, might run an algorithm for 2 seconds, while another computer Y with lesser specifications might take 10 seconds to run the same algorithm.
This shows that measuring the speed of algorithms in real time will create a very big problem, because there would be no definitive way to determine how efficient an algorithm is.
In order to solve this problem, computer scientists created what is known as the Big O Notation.
The Big O notation is just the formalized way of expressing how efficient an algorithm is.
For reasons stated earlier, Big O notation focuses on the number of steps (a constant) an algorithm takes to complete its task rather than the time.
The Big O Notation helps establish the proportionality between the number of steps an algorithm requires and how much the data increases.
To understand the concept better, I’ll be explaining Big O notation using an unordered array (a data structure) and the four (4) basic operations that can be performed on it; Read, Insert, Search, and Delete.
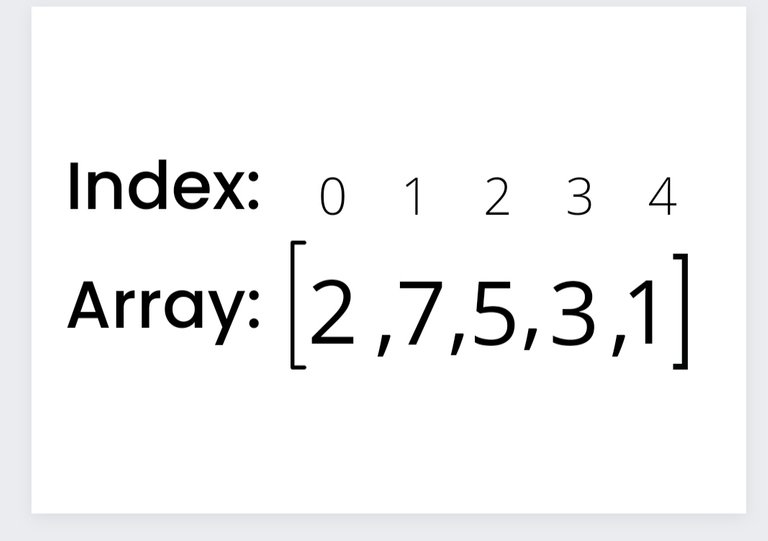
Example of an unordered array
To start off, what is an array?
An array is simply a collection of similar elements. Each of these elements has its own unique index number with the first element having a starting index of 0.

READING

Reading from an array requires just one step no matter the amount of data we have present in the array.
This is because the computer has the index of the required element that needs to be read, and all it needs to do is just go straight to the location where the element is stored and bring it.
This can be expressed in Big O notation as 0(1).
O(1) is used to represent the time complexity of an algorithm that will always need to take a constant amount of steps to carry out an operation.
So, an algorithm that always performs any given task in 10 steps can also be said to have a time complexity of O(1).
Algorithms with O(1) time complexities are generally considered to be more efficient than all other types of algorithm.

SEARCHING

To search for a value in an array takes “N” number of steps. Where “N” is a variable that represents the number of elements that are present in that particular array.
What this means is that, in a worst-case scenario, the computer will have to search through every available data in the array one after the other, before it finds the element it is looking for.
This type of search is known as the Linear search.
Another example of a search algorithm is the Binary search. It is more efficient than the Linear search, but this algorithm can only be applied to an ordered array.
In Big O, Binary search is described as having a time complexity of O(Log N).
Even though the Binary search is more powerful than Linear search algorithm, it isn’t advisable to use it on ordered arrays of small sizes.
A Linear search algorithm is much suited for ordered arrays that are of less sizes.

DELETION

Deleting a data from an unordered array will require the computer to perform “N” number of steps. Removing an element from an array will create an empty space in the array, and arrays don’t allow empty spaces.
To rectify this, the computer will have to adjust the remaining data elements by one step so as to fill up the empty space that was created by what just got deleted.
For example, if we were to delete an element from the beginning of an array containing 10 values, it would take the computer 1 step to delete the item, and 9 more steps to shift the remaining elements in order to eliminate the empty space.
In mathematical terms, it will take;
1 + (N – 1) = N steps.
(where “N” is the number of elements in the array, which in this case is equal to 10)
This means that the Big O notation for deleting from an unordered array can be represented as O(N).

INSERTION

Another operation that can be performed on an array is insertion. Just like the other operations, the number of steps required to insert a new piece of data in an array is dependent on where you want to put it, but we’re only considering the worst-case scenario to measure time complexities.
Using the same example of an unordered array of 10 elements. To insert a new element will require the computer to perform one step, but before inserting, the computer has to create a space for the new item by moving all existing elements by a step to the right.
In mathematical terms, this means that the computer will take:
1 + N = (N + 1) steps
In a worst-case scenario, inserting a new data into an array will require “N + 1” number of steps. Again, “N” is the number of elements that are in the array.
Algorithms are very important in programming and it is always advisable to try to determine how fast your code will run using a particular algorithm before implementing it.
I hope this post helped shed some light on how to determine the efficiency of algorithms using the Big O Notation.
If you have any questions, additions or corrections, do well to put them in the comment section. I’ll be glad to reply.
Thank you for reading.
Man, this is really nice! Guy this thing no enter my head for Altschool but I understood the array part sha.. I go give time digest this your post. Thanks for sharing mate!
Altschool didn't really delve deep into it.
I had to do some extra research on my own before I could understand it.
It's still deeper than this though, but if you can understand everything that is here, comprehending more advanced stuffs won't be too difficult.
Thanks for reading through boss. 🙌🙌
THanks for bringing it! THis is a important concept for basics algorithms!
!1UP
Click this banner to join "The Cartel" discord server to know more.
Thanks for going through it.
And I'll definitely check out The Cartel
you can for example delegate POB tokens to @pob-curator and receive daily passive POB tokens. there are also other tokens that you can delegate for other curators, such as cent, leo, spt, stem
You have received a 1UP from @gwajnberg!
@stem-curator, @vyb-curator, @pob-curator
And they will bring !PIZZA 🍕.
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.
Quite informative. Next time consider adding sources for the reader to check out the content and learn more :)
Oh. I'll definitely do that.
Thanks for stopping by.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @monioluwa! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 4250 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPSupport the HiveBuzz project. Vote for our proposal!
Happy to see you back on here, brother!
And... I have no idea what the heck any of this means 😂
I'll have to wait 'til you write something about psychology or human beings to understand again 😉
Hope you've been well!! 😁
Thank you. It's so good to be back. 😊
I know the feeling. Was once in those shoes. 😂😂. Just felt intrigued and decided to learn what it's all about.
I'll be soon. Working on technical articles like this can be a bit tasking sometimes.
Yeah, I've been very fine. Just taking it all one step at a time.
And what about you?
Trust everything's going well over there too?
And thank you for always looking out for me. I appreciate. It means a lot. 😊😊
Nice one man❤
You really gave a detailed view of the big O Notation. I love the way you broke down each of them with explicit examples.
Tech Odogwu👌
Thanks for stopping by chief.
I still dey learn work from you bosses. 🙌🙌