An XLSref Investigation: Testing Excel's VAR()
How can 5 numbers less than 100 lead to a sample variance over 1000? Is Excel 2003's VAR() bugged? XLSref investigates.
Images are edited screen captures from either Excel 2003 or LeoThreads. Edits made using MS Paint.
Background
In a different life I took a course in statistics. It wasn't a difficult course, but it's a subject whose knowledge escapes if it's not practiced regularly.
It helped having Lotus 1-2-3, the leading spreadsheet app of the day. I used it to produce "work" for each step in solving a problem. It was how I was able to master concepts such as, among other things, standard deviation and sample variance.
Recently at XLSRef (powered by LeoThreads)
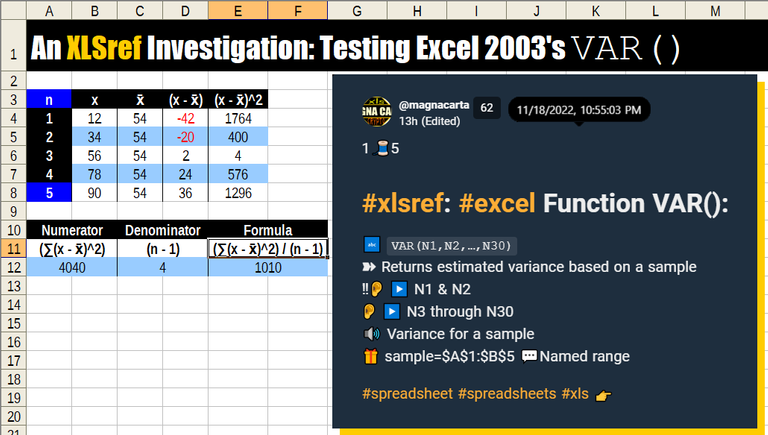
The other day I was preparing the XLSref entry at LeoThreads for function VAR(). Rather than go with the example found in the Excel 2003 Help page for VAR(), I wanted to use a dopey sample-- 12, 34, 56, 78, and 90-- as the XLSref example. To my surprise, VAR() returned 1010 as the sample variance.
Repeatedly I entered that set into the function, and repeatedly 1010 was returned. I used the actual numbers, individual cell address, the range of cells, even a named range. No matter what I did, I kept seeing 1010.
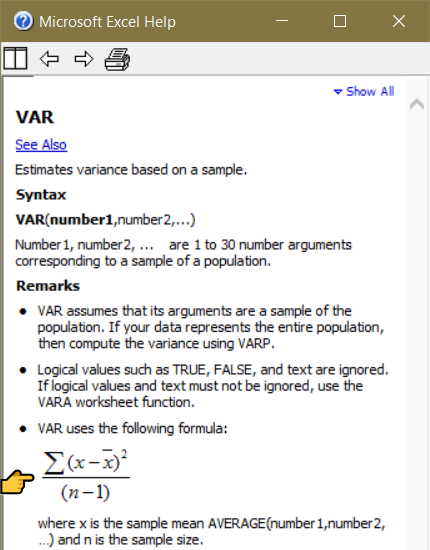
This is how it appeared in Help:
Click to view full-size image
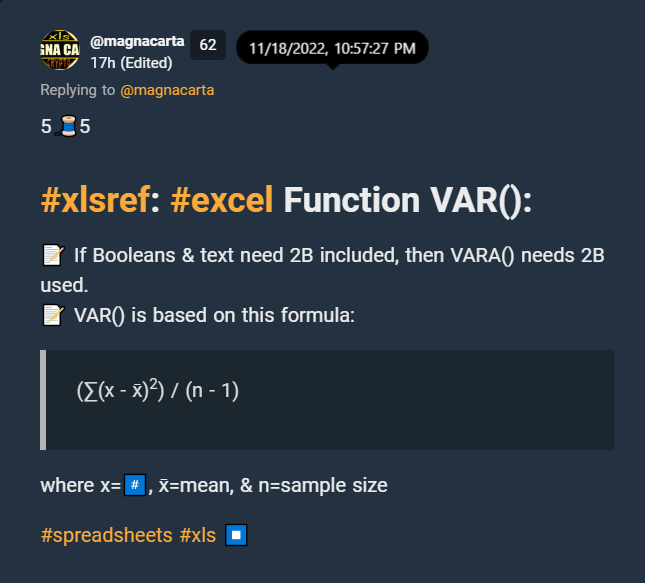
Here is how the formula was translated for XLSref:
Click to view Thread
Something didn't seem right to me, so I needed to see for myself how VAR() came up with such a huge number for my dopey sample.
So I went "back to school" and used Excel 2003 to show myself the work involved in producing the final result.
About Sample Variance
The formula used to calculate sample variance seemed straightforward:
(∑(x - x̄)2) / (n - 1) -- or-- (∑((x - x̄)^2)) / (n - 1)
xis any number in a sample. In this case, any of 12, 34, 56, 78, or 90;x̄is the average (or mean) of all numbers in a sample.nis the size of the sample. For my dopey sample, n=5.
Even the manipulations were straightforward:
(x - x̄)is the difference between a number and the average of the dopey sample. This is where things start getting interesting.- This difference gets squared.
∑(Greek letter Sigma) indicates that squared differences are repeated for each number in the dopey sample, then they are added. Think "for loop" if you code or program.- For the denominator in the formula, it needs to be 1 less than whatever
nis.
With the variables and formula explained, let's see how the "back to school" exercise to test VAR() went for me.
Back to School (Spreadsheet Style)
The cover image shows the 2 tables I set up for my stepwise walthrough of the formula for sample variance.
Here are the same 2 tables in text form:
n | x | x̄ | (x - x̄) | (x - x̄)^2 |
|---|---|---|---|---|
| 1 | 12 | 54 | -42 | 1764 |
| 2 | 34 | 54 | -20 | 400 |
| 3 | 56 | 54 | 2 | 4 |
| 4 | 78 | 54 | 24 | 576 |
| 5 | 90 | 54 | 36 | 1296 |
and
| Numerator | Denominator | Formula |
|---|---|---|
(∑(x - x̄)^2) | (n - 1) | (∑(x - x̄)^2) / (n - 1) |
| 4040 | 4 | 1010 |
In Column A of the first table, several numbers appear for n. The only value which matters is the last value (n=5).
Things To Note:
1️⃣(x - x̄) can be negative.
Sometimes the difference between any number in a sample and the average of all the numbers in a sample. That's OK. Which leads to...
2️⃣Negative numbers squared end up positive.
Remember when teachers cover the use of negatives or double negatives in language? It's the same with math. -2 times -3 = +6.
This is also the explanation for the 1010 result VAR() kept giving me earlier.
3️⃣VAR() needs at least 2 numbers to work properly
If n=1, then denominator (n - 1) ends up as ZERO. Even people who are bad a math remember this detail. (If they didn't, they get reminded by whatever spreadsheet app they use.)
Mystery Solved!
Although I don't claim to know more than the programmers of Excel 2003, I found myself scratching my head at why I saw a result that didn't seem to make sense for the dopey sample of numbers I was using.
I want to trust the app. However, I have no problem taking time to verify how things work. If "Trust, but verify" was good enough for nuclear arms control treaties, it's more than good enough for testing Excel and other apps.
Just My Two Sats
The subject of Statistics seems mystifying, but it makes sense when we step through the math involved at arriving at a result. While the formula for Sample Variance is one of the easier ones in Statistics, the match doesn't make sense until numbers are used.
When I first used VAR() to set up an easy example for XLSref, I was thrown off by the result I kept getting. Just as I did long ago in school, I stepped through each step required of the formula. My stepwise walkthrough of the formula matched what VAR() produced using my numbers.
A large portion of the hundreds of spreadsheet functions are for finance and statistics. Given that these are based on formulas and equations too complex for a microblogging context, I will publish recurring posts featuring my tests and validation ofor some of those formulas and equations.


| Links in image | URLs |
|---|---|
| Hive Business Center | https://ecency.com/created/hive-123507 |
| Hivelist Classifieds | https://ecency.com/created/hive-150840 |
| Hive Hustlers | https://www.hivehustlers.com/ |
| #LeoThreads | https://leofinance.io/threads |
| Hive Projects | https://hiveprojects.io |
| Dust Sweeper | @dustsweeper |
| Dust Bunny | @dustbunny |

| Links in image | URLs |
|---|---|
| "...to make up for..." | https://leofinance.io/hive-167922/@magnacarta/who-is-magnacarta-and-why-is-he-sending-me-pizza |
| LeoFinance | https://leofinance.io/@magnacarta |
| Proof of Brain | https://proofofbrain.blog/@magnacarta |
| ♦ D.Buzz-only ♦ D.Buzz: ♦ at-magnacarta.buzz | https://blog.d.buzz/#/@magnacarta.buzz |
| Festivus | https://festivusweb.com/index.php |
Posted Using LeoFinance Beta
It turned out you needed to visit the old school way to decipher if the Excel was returning the right result or not. It's a good thing to "trust but verify". Well done, Manga.
Interesting! Why did you try with Excel 2003 btw?
It was cheap.
I had been using LibreOffice Calc at home, but I needed to translate menus between Calc at home and Excel at work. Many elements werent where I expected them to be.
I wasn't going to pay full price for the latest version of Excel, but I wasn't going to copy some version, either. So I went old-school and bought Excel 2000 at eBay. Eventually I "upgraded" to Excel 2003.
For most of what I do, Excel 2003 is enough. However, at some point I will need to "upgrade" to Excel 2007 since there are a few things Excel 2003 just can't do.
I still use LibreCalc occasionally, but most people I know or have encountered are familiar with Excel. So I went back to Excel.
Posted Using LeoFinance Beta
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.