Result of the Day 7 Challenge of my May 2021 Math trigonometry mini-contest for D.Buzz 😎
Day 7 Problem
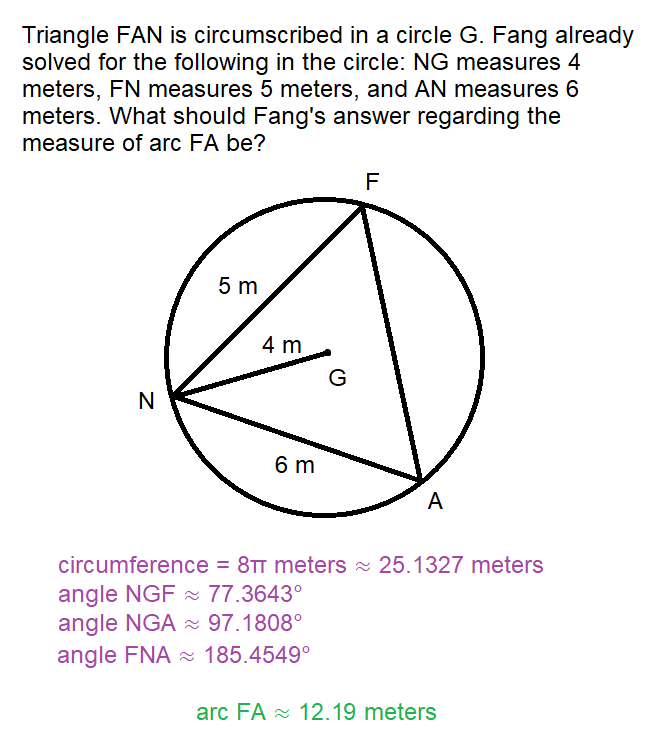
Triangle FAN is circumscribed in a circle G. Fang already solved for the following in the circle: NG measures 4 meters, FN measures 5 meters, and AN measures 6 meters. What should Fang's answer regarding the measure of arc FA be?
This problem was originally posted at https://stemgeeks.net/@savvyplayer/mayday7math.
Answer
12.19 meters 🎯
Equivalent answers in terms of π (which will give an answer of approximately 3.88π) will also be considered correct.
Solution
In this approach, we get the measures of the two other intercepted arcs FN and NA and deduct them from the circumference to get the measure of arc FA.
The circumference of the circle is very easy to get, since we already have the circle's radius which is 4 meters. The circumference is 8π meters or approximately 25.1327 meters.
Triangle NGF has sides NG, FG, and NF, which are 4 meters, 4 meters, and 5 meters, respectively. We can get the measure of arc FN by using the Arc Cosine function together with the Law of Cosines formula. The Law of Cosines is c² = a² + b² - 2 * a * b * cos (C) where cos (C) = (a² + b² - c²) / (2 * a * b), which when inserted to the arccos function gives C = arccos [(a² + b² - c²) / (2 * a * b)] = arccos [(4² + 4² - 5²) / (2 * 4 * 4) ≈ 77.3643°.
Likewise as the last paragraph, triangle NGA has sides NG, FA, and NA, which are 4 meters, 4 meters, and 6 meters, respectively. Using the arccos function together with the Law of Cosines, we get C = arccos [(a² + b² - c²) / (2 * a * b)] = arccos [(4² + 4² - 6²) / (2 * 4 * 4) ≈ 97.1808°
To get the percentage of arc FA to be able to get its actual measure, we need to get the percentage of the circumference occupied by the other two arcs. The two other arcs occupy `(77.3643° + 97.1808°) / 360° ≈ 48.485%. Therefore, arc FA is approximately 51.515% of the circumference of the circle, which has a result of approximately 12.1855 meters.

Winner: @minus-pi 🏅
1 HIVE has been sent to @minus-pi's Hive account. 💰
Despite my Math challenge problems for Day 6 and Day 7 more difficult than usual, @minus-pi was able to solve them correctly!
Mentions: @jfang003, @holovision, @eturnerx (@eturnerx-dbuzz), and @ahmadmanga (@ahmadmangazap) 🤓
Special mentions: @dbuzz, @chrisrice, @jancharlest, and @mehmetfix 🤯
Posted with STEMGeeks
the solution making me dizzyy.. I am out of here! xD
Having a !PIZZA with !LUV would make you less dizzy! 😁
Thanks for stopping by! 😅
@remenzer! I sent you a slice of $PIZZA on behalf of @savvyplayer.
Learn more about $PIZZA Token at hive.pizza (1/10)
my engine is happy with new pizza and luv added! thank you!
You should make your LUV tokens on your Hive Engine wallet reach 10 to be able to give away 3 !LUV per day for free. 😀
Have another !PIZZA too! 🍕😁
@remenzer! I sent you a slice of $PIZZA on behalf of @savvyplayer.
Learn more about $PIZZA Token at hive.pizza (7/10)
I will! Thanks bro!
@remenzer, you were given LUV from @savvyplayer. Info: https://peakd.com/@luvshares or check wallet: https://hive-engine.com
@savvyplayer wants you to have your 10th LUV token, so that you can start sending LUV 3 times daily! 😎
Here is a !LUV for you, with !PIZZA included! ❤️🍕😁
Congratulations on reaching your 10th LUV token! 🎉🎊❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️🎊🎉
@remenzer! I sent you a slice of $PIZZA on behalf of @savvytester.
Learn more about $PIZZA Token at hive.pizza (1/10)
oh my.. thank you so much.. gonna try this later!
@remenzer, you were given LUV from @savvytester. Info: https://peakd.com/@luvshares or check wallet: https://hive-engine.com
@remenzer, you were given LUV from @savvyplayer. Info: https://peakd.com/@luvshares or check wallet: https://hive-engine.com
thanks a lot savvyplayer!! :)