Result of the Day 6 Challenge of my May 2021 Math trigonometry mini-contest for D.Buzz 😎
Day 6 Problem
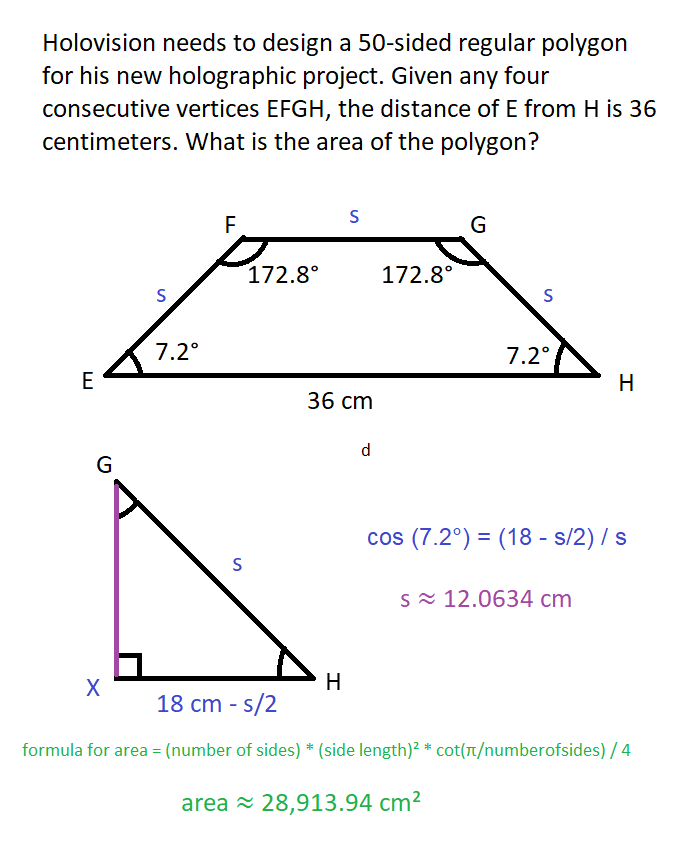
Holovision needs to design a 50-sided regular polygon for his new holographic project. Given any four consecutive vertices EFGH, the distance of E from H is 36 centimeters. What is the area of the polygon?
The problem was originally published at https://stemgeeks.net/@savvyplayer/mayday6math.
Answer
28,914 cm² 🎯
Due to possible rounding off errors, answers very close to that value will be considered correct.
Solution
There are multiple possible solutions to this problem which will give the same answer. This solution is just one of them.
These are the given facts on the original problem:
- The polygon has 50 equal sides.
- The distance between E and H is 36 centimeters.
From those facts, we can obtain the following:
- An interior angle of the polygon measures 172.8°. Angles EFG and FGH have that measure.
- Angles FEG and GHE measure 7.2°, which is the supplementary angle of 172.8°.
From that point, here is the solution:
- Let variable
sbe the measure of any side of the polygon. - Assume there is a line segment GX perpendicular to EH, forming a triangle GXH were X is the right angle and
GH = s. Side HX measures one-half of the difference of the measures of EH ands(you may refer to the image), which is18 cm - s/2. Since we have the measures of GH and XH relative to(valid but unnecessary)s, we can use the Pythagorean theorem to get the measure of GH, also relative tos, which results to√(3s²/4 - 324).- To get the value of
s, we can use the trigonometric ratiocos (x) = (adjacent side) / (hypotenuse), which in our problem iscos (7.2°) = (18 - s/2) / s, which when solved forsgivess ≈ 12.0634 cm.
The formula for the area of a regular polygon given the number of sides and the length of a side, which is the following:
A = n * s² * cot (π/n) / 4
where
- A = area of the regular polygon
- n = number of sides
- s = length of a side
Since we already have the number of sides of the polygon and its side length, we can use the formula above to get the area of the polygon. Note that since there was rounding off in this solution before the final answer was obtained, there are noticeable tiny errors in rounding off.
- A ≈ 50 * 12.0634² * (cot (π/50) / 4
- A ≈ 50 * 145.5256 * 15.8945 / 4
- A ≈ 28913.2897
The more accurate value of the area of the polygon when the equation is directly entered onto a scientific calculator is 28,913.94 (square centimeters). 🤓
Winner: @minus-pi 🏅
1 HIVE has been sent to @minus-pi's Hive account. 💰
This problem was indeed a tough one, but @minus-pi still managed to get the correct answer! 😅
Mentions: @jfang003, @holovision, @eturnerx (@eturnerx-dbuzz), and @ahmadmanga (@ahmadmangazap) 🤓
Special mentions: @dbuzz, @chrisrice, @jancharlest, and @mehmetfix 🤯
Posted with STEMGeeks
thanks, @savvyplayer!
This was a very interesting challenge for me. I'm sorry to see hardly any other participants this time. I think there were quite a couple of participants in April. Maybe people don't like trigonometry?
I won't know what prevented those people from participating my contest until they comment on my posts regarding my Math mini-contest for D.Buzz. 🤔 I think the requirement of "having posted or commented on D.Buzz for the past 72 hours" is too much for potential participants. 😐