Result of the Day 5 Challenge of my May 2021 Math trigonometry mini-contest for D.Buzz 😎
Day 5 Problem
For a triangle DEF whose height is FG and G is on side DE, Manga got
arctan (FG/DG) ≈ 1.176, while Minos gotarctan (FG/GE) ≈ 0.330. What is the minimum possible area of the triangle if FG is an integer?
The problem was originally published at https://stemgeeks.net/@savvyplayer/mayday5math.
Answer
8.6863 square units 🎯
Solution
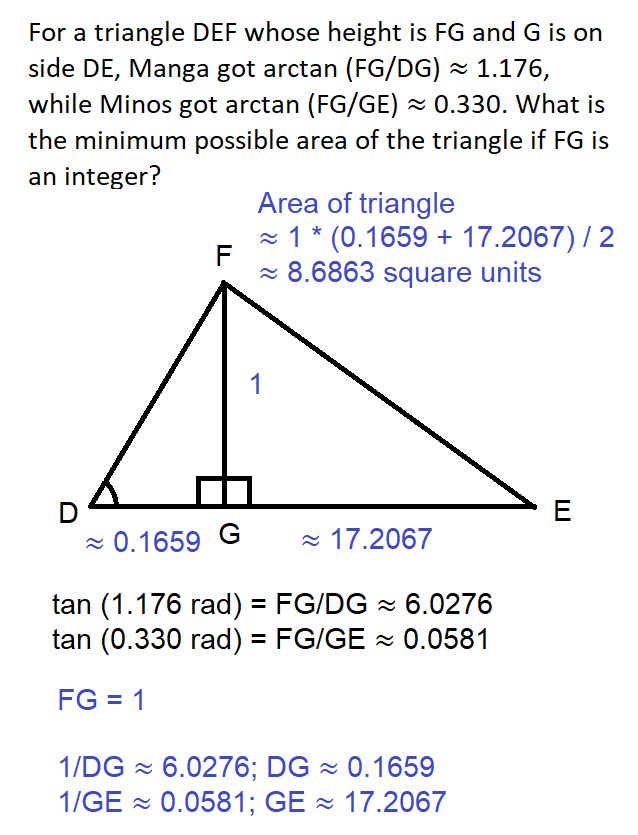
The given states the following:
- arctan (FG/DG) ≈ 1.176 radians
- arctan (FG/GE) ≈ 0.330 radians
- FG is integer
- DE = DG + GE
Based on the given facts above, we can derive the following facts:
- FG/DG = tan (1.176) ≈ 6.0276, so FG ≈ 6.0276 * DG, which gives us DG ≈ 0.1659
- FG/GE = tan (0.330) ≈ 0.0581, so FG ≈ 0.0581 * GE, which gives us GE ≈ 17.2067
- The smaller FG is, the smaller the area of the triangle will be, regardless of the measure of the other sides of the triangle. Therefore, we should set it to 1.
- Since we have assumed FG to be 1, DG * 6.0276 ≈ 1 and GE * 0.0581 ≈ 1, which gives us DG ≈ 0.1659 and GE ≈ 17.2067
- Since DE = DG + GE, DE = 0.1659 + 17.2067 ≈ 17.3727
To get the area of the triangle, we just need its base length and height which are DE and FG, respectively, which we already derived. area = (DE + FG) / 2 ≈ (17.3727 + 1) / 2 ≈ 8.6863 square units.
Winner: none 🤯
Today's prize of 1 HIVE has been split depending on the number of winners in the previous days for this month's contest and sent to the only winning participant so far for this month's Math mini-contest for D.Buzz, which is still @minus-pi! 💰😅
- @minus-pi forgot to add the "square units" again on his answer! 🤯😅
Mentions: @jfang003, @holovision, @ahmadmanga (@ahmadmangazap), and @eturnerx (@eturnerx-dbuzz) 🤓
Special mentions: @dbuzz, @chrisrice, @jancharlest, and @mehmetfix 🤯
Posted with STEMGeeks
lol, again, same mistake 😅
thanks anyway!
Maybe if I was able to show that day's solution quickly after the 24-hour answering period for the Day 4 Math problem, you would have changed your answer for the Day 5 Problem! 🤔😁
Congratulations @savvyplayer! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Check out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!