Result of the Day 4 Challenge of my May 2021 Math trigonometry mini-contest for D.Buzz 😎
Day 4 Problem
Vision knew that the value of tan (2A), where A is one of the acute angles of a right triangle with integer sides, has a value of approximately 1.0084. What is the minimum possible area of the triangle?
This problem was originally published at https://stemgeeks.net/@savvyplayer/mayday4math.
Answer
30 square units 🎯
Solution
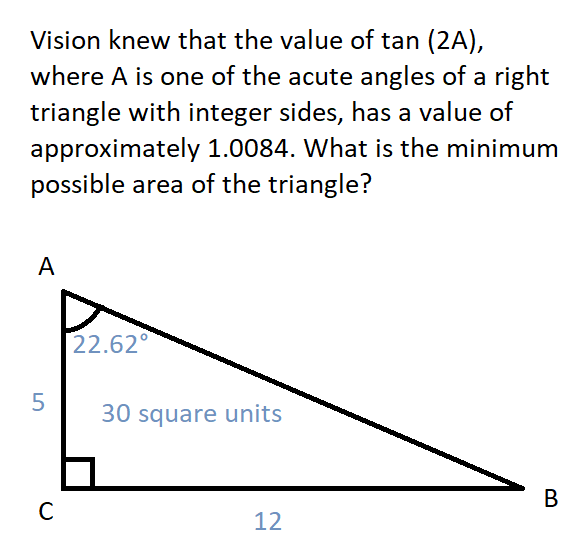
- Sorry for the gritty graphics, because I used MS Paint to draw the image above!* 😅
The given says the following facts:
- tan (2A) ≈ 1.0084
- A is an acute angle
- The triangle has integer sides
Based on the facts above, we can derive the following:
- A ≈ arctan (1.0084) / 2 ≈ 22.6198
- tan (A) ≈ tan (22.6198) ≈ 0.4167
- using geometric series to attempt to convert 0.4167 to fraction, we get 4167/9999 ≈ 5/12
- tan (A) ≈ 5/12
Based on the last derived fact above, the opposite side of the angle is 5 units, and the adjacent side measures 12 units. Since we have the measures of both the legs of the right triangle, we can now use the formula for the area of the triangle, which will give us an area of 30 square units.
Winner: none 🤯
Today's prize of 1 HIVE has been split depending on the number of winners in the previous days for this month's contest and sent to the only winning participant so far for this month's Math mini-contest for D.Buzz, which is no other than @minus-pi! 💰😅
- @minus-pi forgot to add the "square units" on his answer! 🤯 Regardless, he has still received the full prize of 1 HIVE for today because nobody has tried to compete with him so far! 😅
Mentions: @jfang003, @holovision, @ahmadmanga (@ahmadmangazap), and @eturnerx (@eturnerx-dbuzz) 🤓
Special mentions: @dbuzz, @chrisrice, @jancharlest, and @mehmetfix 🤯
Posted with STEMGeeks
lol, true, no value without the according unit - it almost feels like in school 😅
thanks!!
If someone else saw your answer, copied it and just inserted the "square units", they would have won! 🤔😅