Result of the Day 3 [Problem B] Challenge of my July 2021 Math mini-contest for D.Buzz
Day 3 Problem B
Math mini-contest for D.Buzz for July 2021
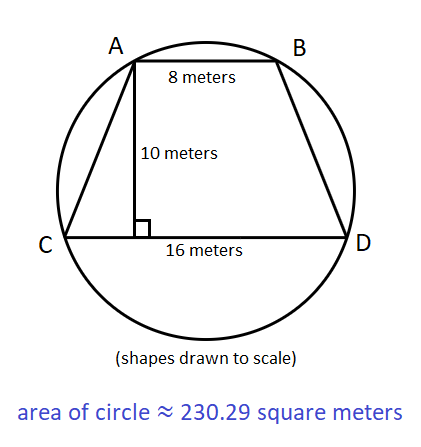
A trapezoid with parallel bases whose lengths are 16 meters and 8 meters has a height of 10 meters. What is the area of the smallest circle that is guaranteed to enclose the trapezoid?
The problem was originally posted at https://stemgeeks.net/@savvyplayer/julymathday3b.
Answer
230.29 square meters
Solution
The smallest circle that can enclose the trapezoid is the circle whose circumference intercept all the vertices of the trapezoid, and that means that the trapezoid's diagonals must be congruent to each other.
Let's start with assigning variables.
- Let the four vertices of the trapezoid be ABCD, where AB measures 8 meters and CD measures 16 meters, and BC and AD are the diagonals of the trapezoid. Since we want the length of each side of the trapezoid to be as close to each other, we should make BC and AD congruent to each other.
- Let O be the center of the circle that encloses the trapezoid.
We can now have the following:
- Triangle ABO is formed by connecting O with A and B. Line segments OA and OB (which are also the radii of the circle) are congruent with each other.
- Triangle CDO is formed by connecting O with C and D. Line segments OC and OD (which are also the radii of the circle) are congruent with each other.
- M is the midpoint of line segment AB. N is the midpoint of line segment CD. Connecting M to N, the length of line segment MN is 10 meters, AM and MB are 4 meters each, and CM and MD are 8 meters each. Since line segment MN passes through circle's center O, the sum of the lengths of line segments MO and ON is 10 meters. We will then represent the measure of line segment MO as
x, and line segment ON as10 - x. - We now have a triangle AMO, where AM is 5 meters, MO is
xmeters, and OA is the radius of the circle. We can use triangle BMO for this, since the two triangles are congruent. - We also have the triangle CMO, where CM is 8 meters, MO is
10 - xmeters, and OC is the radius of the circle. We can use triangle DMO for this. - Since the triangles AMO and CMO have congruent hypotenuses which correspond to the radii of the circle, we can combine them into one equation.
- Let
rbe the radius of the circle, which can be OA, OB, OC, or OD.
For triangle AMO, AO² = AM² + MO²or r² = 5² + x². For triangle CMO, CO² = CM² + MO² or r² = 8² + (10 - x)². Since one side of either equation equals r², we can combine them into one equation.
- 5² + x² = 8² + (10 - x)²
- x² + 25 = x² - 20x + 164
- 20x = 139
- x = 6.95
We now have the distance of each base of the trapezoid from the center of the circle. However, we still need to get the radius of the circle. To get the value of the radius, we should substitute 6.95 for x on either equation of triangle AMO or CMO. In this case, we choose AMO because its equation is more simple.
- r² = 5² + x²
- r² = 5² + (6.95)²
- r² = 73.3025
- r ≈ ±8.5617
Since there is no such thing as negative distances, we get only the positive value of the radius, which is approximately 8.5617 meters. Nevertheless, we can insert the value of r² directly to the formula for the area of the circle.
Since we now have the radius of the circle, we just need to insert it to the formula for the area of the circle.
- area = π * radius²
- area = π * 73.3025
- area ≈ 230.2866
The area of the smallest circle that can enclose the trapezoid is approximately 230.29 square meters.
Winner: none
1 HIVE has been transferred to the prize pool, which will be awarded to the participant with the highest number of correctly-answered problems after all the challenge problems in this Math mini-contest for July 2021 have been concluded.
I still need to prepare a non-programming solution for my Day 1B Problem on this post, which is the last challenge problem I need to conclude to give away the prize pool. If I could not prepare a purely mathematical solution soon, I would just show the programming solution for the problem, and everyone who tried to answer that problem will receive 1 HIVE as compensation for their efforts in trying to solve the problem conventionally.
Mentions: @jfang003, @holovision, @eturnerx (@eturnerx-dbuzz), @ahmadmanga (@ahmadmangazap), @appukuttan66, @paultactico2, @dkmathstats, @lolxsbudoy, and @minus-pi
Special mentions: @dbuzz, @chrisrice, @jancharlest, and @mehmetfix
Posted with STEMGeeks
I upvoted you, thank you for posting!
Have a !PIZZA with !LUV for all your Math work.
Posted via D.Buzz
<><
@savvyplayer, you've been given LUV from @ahmadmangazap.
Check the LUV in your H-E wallet. (5/10)
@savvyplayer! I sent you a slice of $PIZZA on behalf of @ahmadmangazap.
Learn more about $PIZZA Token at hive.pizza (5/10)
Thanks for your appreciation.
Because the lack of participants happened a second time, I have decided not to host Math contests anymore (at least for this year) until there is a large increase in Hive users interested in Math.
I won't say that's a bad idea, but the only reason I don't take part is that they cost me a lot of time and brain power. Otherwise I love trying my hand on math.
Good Luck!
!LUV !PIZZA
Posted via D.Buzz
<><
@savvyplayer, you've been given LUV from @ahmadmangazap.
Check the LUV in your H-E wallet. (1/10)
@savvyplayer! I sent you a slice of $PIZZA on behalf of @ahmadmangazap.
Learn more about $PIZZA Token at hive.pizza (2/10)
Maybe hosting online Math contests should be done somewhere else, not here on Hive where it looks like people are much more focused on creating content rather than reading content.
The sad thing is that I totally agree...
Posted via D.Buzz