The curve xy = k and its significance
Recently I have been looking at automatic market makers (AMMs), and have opened the hood into the maths and algorithms behind these. In the future I plan on doing a post on how these work, but I thought as a precursor I would do a post explaining the key formula behind AMMs, and that is
xy=k
Formula structure
Normally, people are comfortbale with functiosn and grapsh when they are expressed as a function of x. For example
y = f(x)
However in this case we have x and y on the same side. If you prefer that form, its easy to convert, just divide by x on both sides, the formula becomes
y = k/x
But why express it as xy=k if that's more complicated to intuitively understand. Well in my view its the application. the AMMs ensure the multiplication of the reserves form both coins always stays the same, so its much easier to think formula the formula like this.
What does the graph look like
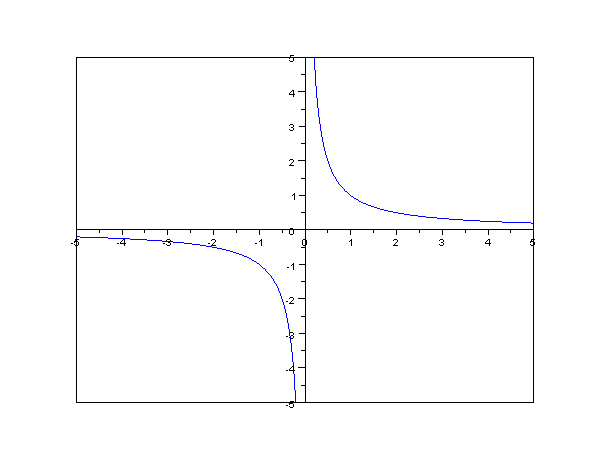
Source: Wikipedia https://en.wikipedia.org/wiki/Proportionality_(mathematics)
Why are there two separate lines?
You might see that the graph fills two quadrants, the top left and the bottom right. At first this might seem a bit confusing but lets take an example
if xy = 10, then one point on the curve is (5,2) , because 5*2 = 10
however =(-5,-2) is also on the curve because (-5) * (-2) also equals 10.
It's interesting to note, that often in real world problems we only need to look at the top quadrant, because in the example of an AMM, we don't have negative reserves to multiply out.
What are some other applications of xy=k
There are numerous examples, but one that comes to mind, is where you have a fixed area for a rectangle, but you can adjust the width and height as desired. using the formula xy=k, where the k is the area and x and y are the width and heights respectively.
There would be countless problems that require this maybe you are creating a garden but only have a certain amount of soil to cover an area, so you can use the formula to work out the options for the dimensions. there are countless more examples.
Comment below if you have any good applications of this formula
Yay! 🤗
Your content has been boosted with Ecency Points, by @notak.
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for Proposal
Delegate HP and earn more
I was hoping someone would through a graph in front of me before I even have coffee today. 😆
Thanks a lot, !BRO
maths isn't everyone's cup of tea... but glad it was the appetizer to your coffee!
It was ok, but I think it goes better with !BEER and !PIZZA
PIZZA Holders sent $PIZZA tips in this post's comments:
@sinistry(3/10) tipped @notak (x1)
Learn more at https://hive.pizza.