KNOWING SINE RULE
Hello math bugs(🐞) & hivers(🐝)
I hope you are strong and stout and doing good in life.
Well come back to another intersting problem.We gonna find the solution using sine rule.If you have less knowledge about cir-cum-centre or cir-cum-circle of a triangle, must check details here. Because without it we can't go further.
We need to find out BO and what we have been given is AB= 4 cm and opposite angle of AB i.e ∠c= 30°.You can check it in the figure below.I hope now you are well familiar to cir-cum-circle or It's centre.Other than knowledge of this what we need to know is Sine rule. So I am gonna proof sine rule first then the solution will become lucid.

In the following figure angle BOC is two times of angle A.The perpendicular on the mid point of side BD divide angle BOC into two equal half and each of them is equal to angle A.Now from ∆BOD , we can find sinA. Check what we got in the following figure.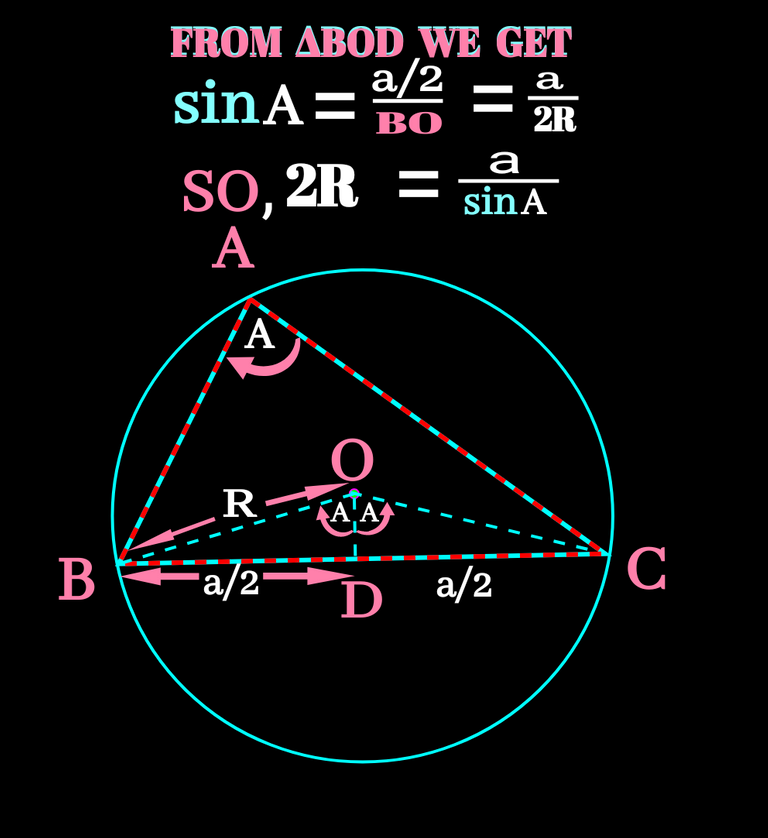
Must know all BO, AO & CO are equal to Cur-cum-radius(R).
Again angle AOC is twice the angle B. The same as previous case here also angle AOC got divided into two equal half and each equals to angle B. Now from ∆ADO we get sinB. Check it in the following figure.
We can draw cir-cum-circle in every figure but for simplicity I have done it for the first one only.
Again angle AOB is twice the angle C And perpendicular EO on AB touches centre and thus the isosceles ∆ABO gets divided into equal half.Thus angle AOB gets divided into two half again as previous case and each equals to angle C. Check below how can we get sinC again from ∆AEO
In all cases the two cir-cum-radius and a side of the triangle will make an isocelles triangle
The result from the final three figure above we can reach the conclusion that double of cir-cum-radius is always equal to the ratio of a side of a triangle and the sin-ratio of it's opposite angle.check the final result below.
Finally the solution has become very easy as we got and equation where variables are R , a side of triangle and sin-ratio of opposite angle of the side.In the problem we are provided by two of them and so we reach the solution. Check it in the figure below.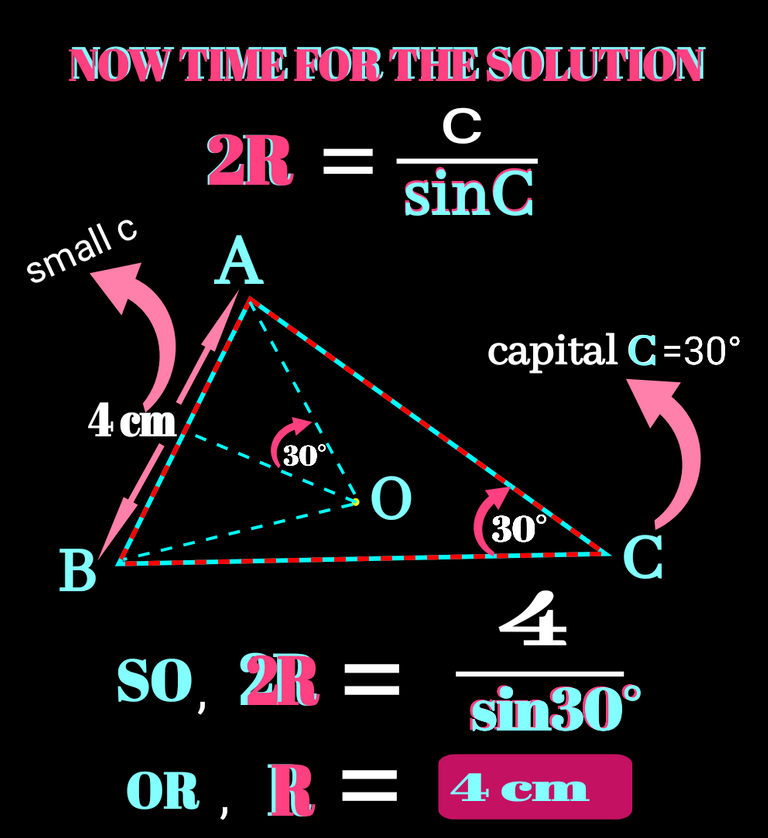 BO is equals to R and so the solution is 4 cm.
BO is equals to R and so the solution is 4 cm.
I am planning to write about cosine rule also in my next post.Hehe till then bye bye.
I hope you enjoyed it.
Thanks for the visit.
All is well.
Regards: @meta007
Congratulations @meta007! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 7000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Well described. It seems like that somebody teaching me a lesson of math instead of having knowledge about this topic 😂.
😃😃 I am flattered.I try to explain things in lucid way. Thanks man for your kind words.
This would help a lot of school students !
Great work !
It seems in school things were tough that today😅.Thanks man for visiting.
This post has been manually curated by @bhattg from Indiaunited community. Join us on our Discord Server.
Do you know that you can earn a passive income by delegating to @indiaunited. We share 100 % of the curation rewards with the delegators.
Here are some handy links for delegations: 100HP, 250HP, 500HP, 1000HP.
Read our latest announcement post to get more information.
Please contribute to the community by upvoting this comment and posts made by @indiaunited.
This is a very good explanation and proof.
!discovery 41
It's nice to have a comment from you.
Thanks man for visiting.
This post was shared and voted inside the discord by the curators team of discovery-it
Join our community! hive-193212
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @meta007! You received a personal badge!
Wait until the end of Power Up Day to find out the size of your Power-Bee.
May the Hive Power be with you!
You can view your badges on your board and compare yourself to others in the Ranking
Check out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Congratulations @meta007! You received a personal badge!
Participate in the next Power Up Day and try to power-up more HIVE to get a bigger Power-Bee.
May the Hive Power be with you!
You can view your badges on your board and compare yourself to others in the Ranking
Check out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!