Thomas Method using Python

There are several methods to solve for the values of x, y, and z in the system of equations. Among these methods is LU Factorization Methods. One of these methods is Thomas Method. Initially, represent the system of equation as a matrix of its coefficients, variables and constants.

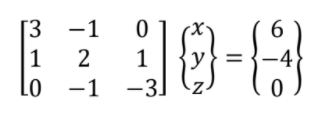
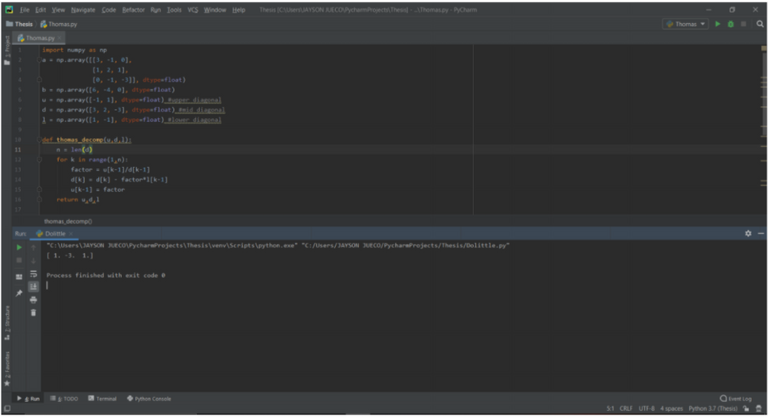
To initialize the recipe in python, we first convert the matrix representation of these equations as arrays. This can be done by declaring two set of arrays: (a) for the coefficients of the system of equations, and (b) for the constant. Each arrays are assigned as a floating point value.

a = np.array([[3, -1, 0],
              [1, 2, 1],
              [0, -1, -3]], dtype=float)

b = np.array([6, -4, 0], dtype=float)

With Gauss and Doolittle, we setup two set of arrays a and b; but for Thomas, 5 arrays are needed. The additional arrays are for the upper, lower and mid diagonal of the coefficient matrix.

u = np.array([-1, 1], dtype=float) #upper diagonal
d = np.array([3, 2, -3], dtype=float) #mid diagonal
l = np.array([1, -1], dtype=float) #lower diagonal

The upper, mid and lower diagonal elements are used to transform a new coefficient matrix. The decomposition follows the algorithm where the values of the new mid diagonal is equal to its old values subtracted with the ration of the upper and mid diagonal. In python repetition of steps can be performed through a for loop.

for k in range(1,n):
    factor = u[k-1]/d[k-1]
    d[k] = d[k] - factor*l[k-1]
    u[k-1] = factor

We define a decomposition function based on the algorithm mentioned earlier. The function returns new set of diagonal values. This new values can be used for forward and backward substitution to solve for the unknown variables.

def thomas_decomp(u,d,l):
     n = len(d)
     for k in range(1,n):
          factor = u[k-1]/d[k-1]
         d[k] = d[k] - factor*l[k-1]
         u[k-1] = factor
     return u,d,l

Similar to Doolittle, the forward and backward substitution is done with the same algorithm. The function enclosing the algorithm would return the values for the unknown variables in the system of equations.

def thomas_solve(u,d,l,b):
n = len(d)
for k in range(1,n):
      b[k] = b[k] - u[k-1]*b[k-1]
b[n-1] = b[n-1]/d[n-1]
for k in range(n-2,-1,-1):
      b[k] = (b[k] - l[k]*b[k+1])/d[k]
return b

The full implementation of the Thomas Method combines both the decomposition and the solver function.

for k in range(1,n):
    factor = u[k-1]/d[k-1]
    d[k] = d[k] - factor*l[k-1]
    u[k-1] = factor

u = np.array([-1, 1], dtype=float) #upper diagonal
d = np.array([3, 2, -3], dtype=float) #mid diagonal
l = np.array([1, -1], dtype=float) #lower diagonal

def thomas_decomp(u,d,l):
     n = len(d)
     for k in range(1,n):
          factor = u[k-1]/d[k-1]
         d[k] = d[k] - factor*l[k-1]
         u[k-1] = factor
     return u,d,l

def thomas_solve(u,d,l,b):
     n = len(d)
     for k in range(1,n):
          b[k] = b[k] - u[k-1]*b[k-1]
     b[n-1] = b[n-1]/d[n-1]
     for k in range(n-2,-1,-1):
          b[k] = (b[k] - l[k]*b[k+1])/d[k]
     return b