Gaussian Elimination in Python
There are several methods to solve for the values of x, y, and z in the system of equations. Among these methods is Gauss Elimination. It is a method wherein it reduces the matrix of the system of equation into its upper triangular system. For the system of equations mentioned earlier, it can be represented in a matrix.
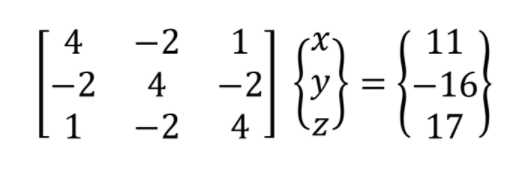
An easier way to implement find out the solution set for a system of equations is to write a recipe following the Gauss elimination algorithm. To initialize the recipe in python, we first declare the matrix representation of these equations as arrays. This can be done by declaring two set of arrays: (a) for the coefficients of the system of equations, and (b) for the constant. Each arrays are assigned as a floating point value.
a = np.array([[4, -2, 1],
[-2, 4, -2],
[1, -2, 4]], dtype = float)
b = np.array([11, -16, 17], dtype = float)
The initial phase of the Gauss elimination algorithm is to perform forward elimination. The initial step for the forward elimination is to eliminate the first unknown variable in the second through the nth equations. This can be done by multiplying the quotient of [col 1, row 2] and [col 1, row 1]. After its execution, subtract the result to all elements in row 2 of the matrix.
In the recipe, this can be done by running a for loop which performs the said steps until all lower triangular elements in the matrix becomes zero. For the loop to stop a conditional statement is inserted inside the loop. The if condition determines that there should be that the nth row should not have an all zero element.
for k in range(0,n-1): #k is matrix row
for i in range(k+1,n): #i is matrix col
if a[i,k] != 0.0:
factor = a[i,k]/a[k,k]
a[i,k+1:n] = a[i,k+1:n] - np.multiply(factor,a[k,k+1:n])
b[i] = b[i] - np.multiply(factor,b[k])
The second phase for the gauss elimination algorithm is back substitution. In this part nth variable is solve by diving the coefficient at [nth col, nth row] in the matrix. With the solve nth variable value, this is feed to the (n-1) row to solve for the (n-1) variable. To implement the back substitution in python, a for loop is run until all variables has a value.
for k in range(n-1,-1,-1):
b[k] = (b[k] - np.dot(a[k,k+1:n],b[k+1:n]))/a[k,k]
Now, both forward elimination and back substitution has been implemented. We define a new function for the Gauss Elimination so that code run efficiently. This is also done so that we do not need to recode both forward elimination and back substitution algorithm.
def gauss_method(a,b):
n = len(b) #n is matrix size
#Elimination phase
for k in range(0,n-1): #k is matrix row
for i in range(k+1,n): #i is matrix col
if a[i,k] != 0.0:
factor = a[i,k]/a[k,k]
a[i,k+1:n] = a[i,k+1:n] - np.multiply(factor,a[k,k+1:n])
b[i] = b[i] - np.multiply(factor,b[k])
#Back substitution
for k in range(n-1,-1,-1):
b[k] = (b[k] - np.dot(a[k,k+1:n],b[k+1:n]))/a[k,k]
return b
To run the code, we need to compile both declaration of the system of equation matrix and Gauss elimination algorithm.
def gauss_method(a,b):
n = len(b) #n is matrix size
#Elimination phase
for k in range(0,n-1): #k is matrix row
for i in range(k+1,n): #i is matrix col
if a[i,k] != 0.0:
factor = a[i,k]/a[k,k]
a[i,k+1:n] = a[i,k+1:n] - np.multiply(factor,a[k,k+1:n])
b[i] = b[i] - np.multiply(factor,b[k])
#Back substitution
for k in range(n-1,-1,-1):
b[k] = (b[k] - np.dot(a[k,k+1:n],b[k+1:n]))/a[k,k]
return b
#Declare matrices
a = np.array([[4, -2, 1],
[-2, 4, -2],
[1, -2, 4]], dtype = float)
b = np.array([11, -16, 17], dtype = float)
x = gauss_method(a,b)
#A = nxn coefficient matrix
#b = nx1 result vector
#Ouput Matrix
print(x)
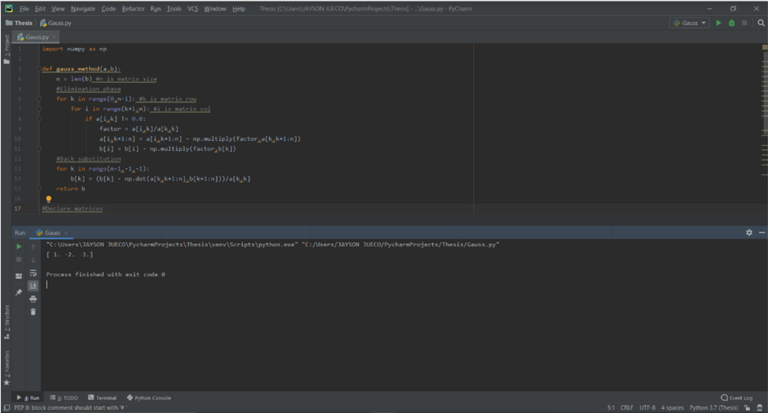
After running the recipe, we obtain the values of x, y, and z as 1, −2, and 3 respectively. The result of running the code is shown below. The result is shown in cover image.
Posted with STEMGeeks