Citizen Science Episode 6
Citizen Science Entry 6
I'm on the last released episode of LeMouth's citizen science. Woo!
The complete citizen science tour took about a month. I learned a bit about subatomic physics and I even know how to simulate collisions for the LHC. Not bad!
Anyways, let's get started. Next up is @lemouth's episode 6. In this episode we address uncertainties. A topic most near and dear to my heart.
"The quest for certainty blocks the quest for meaning." - Erich Fromm.
A working directory for LO simulations
Let's reanimate madgraph5 as no installations are needed today. We've already installed the heavyN neutrino mass model in episode 5.
$ cd ~/physics/MG5_aMC_v2_9_9
$ ./bin/mg5_aMC
MG5_aMC>import model SM_HeavyN_NLO
MG5_aMC>define p = g u c d s u~ c~ d~ s~
MG5_aMC>define j = p
MG5_aMC>generate p p > mu+ mu+ j j QED=4 QCD=0 $$ w+ w- / n2 n3
MG5_aMC>add process p p > mu- mu- j j QED=4 QCD=0 $$ w+ w- / n2 n3
MG5_aMC>output ep6_lo
MG5_aMC>launch
These steps mirror those taken in episode 5. After launch completed, the cross-section calculated was s = 0.013824 ± 4.55e-05 (pb).
As per my entry for episode 5, I generated diffs for param_card.dat and run_card.dat. I used the diffs to double check my changes but I'll spare you the details of the diffs.
Per the output of madgraph5, I set my LD_LIBRARY_PATH environment variable to ensure lhapdf ran properly. Without it, no scale or PDF variation is visible in madgraph's output. Here's the command I used:
LD_LIBRARY_PATH=~/physics/MG5_aMC_v2_9_9/HEPTools/lhapdf6_py3/lib ./bin/mg5_aMC
Assignment
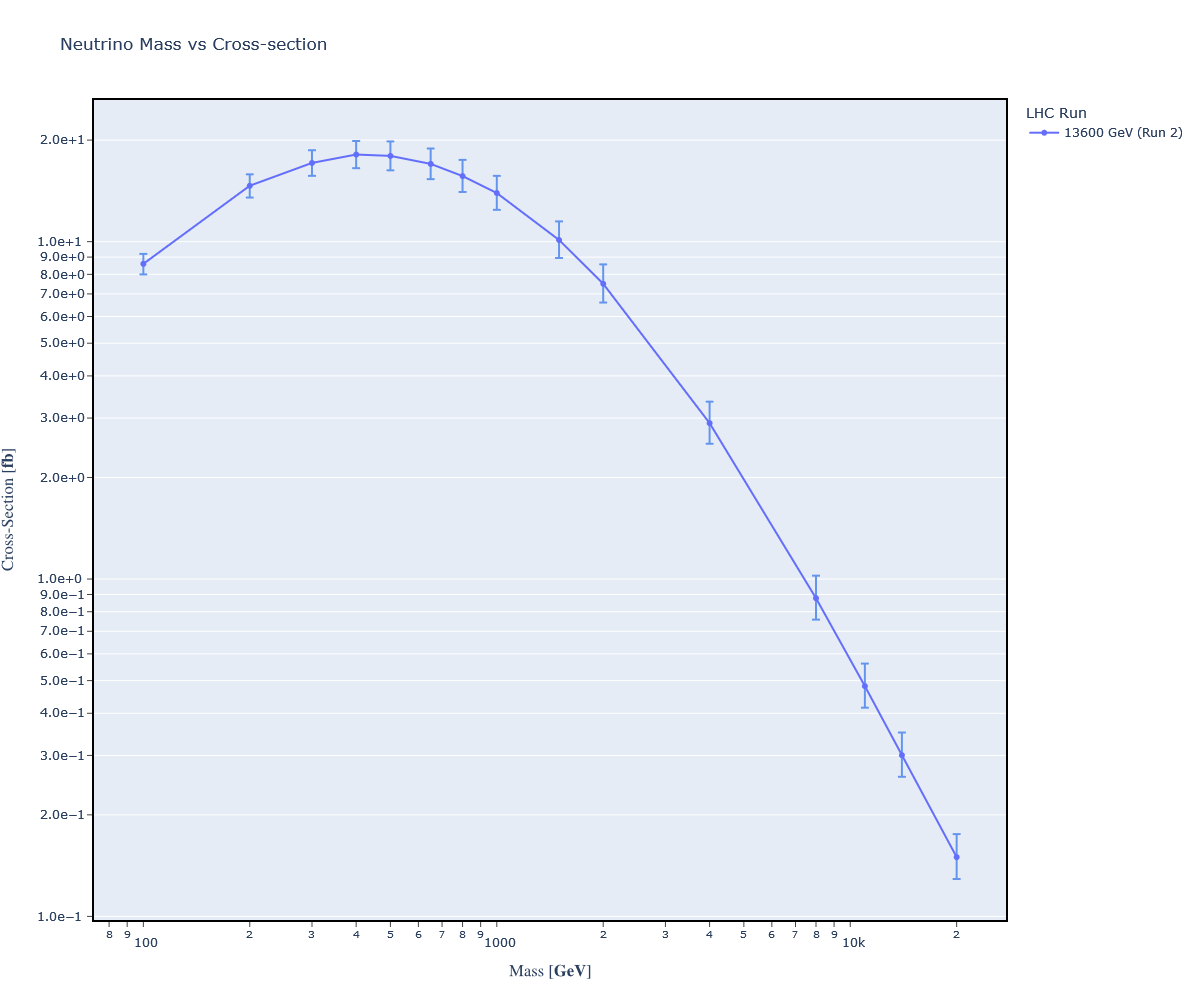
Today's assignment is to redo the calculations we performed in episode 5. But, this time, we'll include data on uncertainty. We want to understand the precision of our datapoints, assuming that there is no systemic error reducing our accuracy.
To understand our precision, we'll be paying attention to 'scale variation' and 'PDF variation'. Both are given as a percent uncertainty in the terminal output of madgraph5. The madgraph5 stdout looks like this:
=== Results Summary for run: run_25 tag: tag_1 ===
Cross-section : 0.01394 +- 4.458e-05 pb
Nb of events : 10000
INFO: Running Systematics computation
INFO: Idle: 2, Running: 2, Completed: 0 [ current time: 11h25 ]
INFO: Idle: 0, Running: 3, Completed: 1 [ 14.7s ]
INFO: # events generated with PDF: NNPDF30_lo_as_0118 (262000)
INFO: #Will Compute 145 weights per event.
INFO: #***************************************************************************
#
# original cross-section: 0.01393212078168743
# scale variation: +11% -9.16%
# central scheme variation: + 0% -36%
# PDF variation: +5.78% -5.78%
#
# dynamical scheme # 1 : 0.00996038 +8.01% - 7% # \sum ET
# dynamical scheme # 2 : 0.00996038 +8.01% - 7% # \sum\sqrt{m^2+pt^2}
# dynamical scheme # 3 : 0.0107584 +8.56% -7.42% # 0.5 \sum\sqrt{m^2+pt^2}
# dynamical scheme # 4 : 0.00891454 +7.18% -6.37% # \sqrt{\hat s}
#***************************************************************************
Here, we see the scale variation percentage is: +11% (upper) and -9.16% (lower). The PDF variation is +5.78% (upper) and -5.78% (lower). Per lemouth's guidance, we can add the upper and lower terms in quadrature. Quadrature is akin to finding the hypotenuse of a right triangle, or finding the length of a vector in euclidean space. For example, to find the total upper percentage of uncertainty of the output given above, we'd perform the following calculation:
sqrt(11^2 + 5.78^2) = 12.4%
Note that hidden in this quadrature calculation is an assumption: both scale and PDF variation errors are independent of one another.
How do we graph this error? All we need to do is multiply the percent uncertainty against the cross-section to obtain the absolute uncertainty. For example, in the above we have: .124 * 0.0139 pb = 0.00172 pb.
Here's the resulting graph:
Conclusions
That was a pretty quick episode as we heavily leveraged our prior work in episode 5.
Anyways, I'll hopefully see all you beautiful people around soon!
Enjoy physics. :)
Posted with STEMGeeks
Congratulations @iauns! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 20 posts.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Check out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Dear @iauns, sorry to jump in a bit off-topic.
May I ask you to review and support the new proposal (https://peakd.com/me/proposals/240) so I can continue to improve and maintain this service?
You can support the new proposal (#240) on Peakd, Ecency, Hive.blog or using HiveSigner.
Thank you!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.