Physics - Classical Mechanics - Damped Oscillation
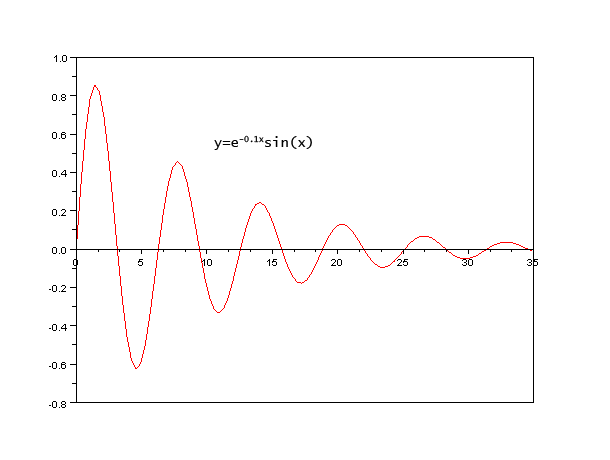
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Physics, and more specifically the branch of "Classical Mechanics" in order to get into Damped Oscillation.
So, without further ado, let's get straight into it!
Damped Oscillation
The period motions that we've covered up to this point were all ideal, with no friction. In real systems, there is always a force that "damps" down the oscillator, eventually stopping the oscillation completely.
Damping Force
These damping forces can become quite complicated. The simplest one which is kinetic friction only depends on the velocity, so let's use this one for our model.
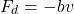
In this equation b is the damping constant or coefficient, which specifies the strength of the damping.
Total Force and Differential Equation
Adding this force to the simple harmonic motion model, yields:
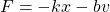
Of course, from Newton's 2nd Law this also equals ma. Let's also introduce derivatives of x. This gives us the following quadratic differential equation:
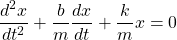
Motion Equations
The solution to the previous differential equation is known. It's an oscillating cosine in the envelope of an exponential function, an exponentially decaying sinusoidal. Thus, the displacement in a damping oscillation is given by:
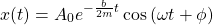
The corresponding angular frequency (ω) is:
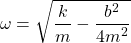
Substituting SHM's angular frequency, which is referred to as the natural angular frequency (ω0), yields:
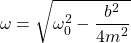
Special Cases
Depending on the value of b, there are three cases for an Damping Oscillator:

As b increases ω eventually reaches zero. If it increases even further it becomes a complex number.
In an underdamped system the amplitude decreases exponentially, eventually putting the system to rest. When equal to zero (critical damping), the system doesn't oscillate at all. And lastly, an overdamped system takes much longer to reach equilibrium than the other two and also doesn't oscillate.
More specifically, for the last case, the solution can also be written as:

This is the same behavior as electronic circuits!
RESOURCES:
References
- https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/15-5-damped-oscillations/
- https://webhome.phy.duke.edu/~rgb/Class/phy51/phy51/node24.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/oscda.html
Images
Mathematical equations used in this article, where made using quicklatex.
Visualizations were made using draw.io.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
- Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Internal Energy and Work -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Angular Motion
- Angular motion basics -> Angular position, velocity and acceleration
- Rotation with constant angular acceleration -> Constant angular acceleration, Example
- Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
- Parallel Axis Theorem -> Parallel axis theorem with example
- Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
- Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
- Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
- Angular Momentum -> Angular Momentum and its conservation
- Explaining the Physics behind Mechanical Gyroscopes -> What they are, History, How they work (Precession, Mathematical Analysis) Difference to Accelerometers
- Exercises around Angular motion -> Angular motion examples
Equilibrium and Elasticity
- Rigid Body Equilibrium -> Equilibrium Conditions of Rigid Bodies, Center of Gravity, Solving Equilibrium Problems
- Force Couple System -> Force Couple System, Example
- Tensile Stress and Strain -> Tensile Stress, Tensile Strain, Young's Modulus, Poisson's Ratio
- Volumetric Stress and Strain -> Volumetric Stress, Volumetric Strain, Bulk's Modulus of Elasticity, Compressibility
- Cross-Sectional Stress and Strain -> Shear Stress, Shear Strain, Shear Modulus
- Elasticity and Plasticity of Common Materials -> Elasticity, Plasticity, Stress-Strain Diagram, Fracture, Common Materials
- Rigid Body Equilibrium Exercises -> Center of Gravity Calculation, Equilibrium Problems
- Exercises on Elasticity and Plasticity -> Young Modulus, Bulk Modulus and Shear Modulus Examples
Gravity
- Newton's Law of Gravitation -> Newton's Law of Gravity, Gravitational Constant G
- Weight: The Force of Gravity -> Weight, Gravitational Acceleration, Gravity on Earth and Planets of the Solar System
- Gravitational Fields -> Gravitational Field Mathematics and Visualization
- Gravitational Potential Energy -> Gravitational Potential Energy, Potential and Escape Velocity
- Exercises around Newtonian Gravity (part 1) -> Examples on the Universal Law of Gravitation
- Exercises around Newtonian Gravity (part2) -> Examples on Gravitational Fields and Potential Energy
- Explaining the Physics behind Satellite Motion -> The Circular Motion of Satellites
- Kepler's Laws of Planetary Motion -> Kepler's Story, Elliptical Orbits, Kepler's Laws
- Spherical Mass Distributions -> Spherical Mass Distribution, Gravity Outside and Within a Spherical Shell, Simple Examples
- Earth's Rotation and its Effect on Gravity -> Gravity on Earth, Apparent Weight
- Black Holes and Schwarzschild Radius -> Black Holes (Creation, Types, How To "See" Them), Schwarzschild Radius
Periodic Motion
- Periodic Motion Fundamentals -> Fundamentals (Period, Frequency, Angular Frequency, Return Force, Acceleration, Velocity, Amplitude), Simple Harmonic Motion, Example
- Energy in Simple Harmonic Motion -> Forms of Energy in SHM (Potential, Kinetic, Total and Maximum Energy, Maximum Velocity), Simple Example
- Simple Harmonic Motion Equations -> SHM Equations (Displacement, Velocity, Acceleration, Phase Angle, Amplitude)
- Simple Harmonic Motion and Reference Circle -> SHM and Smooth Circular Motion, Reference Circle
- Simple Harmonic Motion Exercises -> 2 Complete Examples on Simple Harmonic Motion
- Simple Pendulum -> Simple Pendulum (Return Force, Small Angle Approximations, More Accurate Period, Gravity Approximation)
- Physical Pendulum -> Physical Pendulum (Return Torque, Small Angle Approximations, Estimating Moment of Inertia)
- Exercises around Pendulums -> Complete Examples on the 2 types of Pendulums (Simple, Physical)
Final words | Next up
And this is actually it for today's post!
Next time we will get into Forced Oscillation and Resonance...
See ya!

Keep on drifting!
Posted with STEMGeeks
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.