Mathematics - Number Theory - Introduction

[Image 1]
Introduction
Hey it's a me again @drifter1!
I was quite busy with many things during the last weeks, but yeah now I'm back...
Today we continue with Mathematics, in order to start with a new series, a series on the branch of mathematics known as "Number Theory". Such a series was promised during the "Discrete Mathematics" series, which I highly suggest you to check out as well.
This article will be a small introduction to what Number theory is all about and will give you a quick overview of all the topics that will be covered during the series.
So, without further ado, let's dive straight into it!
Number Theory
Number theory is the study of natural numbers (or positive integers). There are many problems which involve only basic additions and multiplications of such numbers. Of course, this doesn't mean that solving such problems is always an easy task. To the contrary, there are basically infinite mathematical problems related to natural numbers which are still unsolved or require quite complicated math in order to get at least an approximate answer.
Ancient Greece
Counting with natural numbers dates back to the prehistoric ages, but the first general theories of numbers started in Ancient Greece through non other than Pythagoras, Euclid and Diophantus.
For example, Pythagoras worked with pairs of integers which he called "amicable". Two integers are called so if they are equal to the sum of the proper divisors of the other, such as 220 and 284:
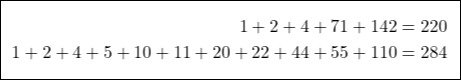
On the other hand, Euclid provided us with the basic factorization of numbers through his division algorithm.
Diophantus studied various mathematical problems, but the one with the most significance is non other than the so called Diophantine equations, which are equations whose solutions must be whole numbers.
Asia
Going further two the East we should not forget to mention:
- the Chinese remainder theorem from Qin Jiushao
- the Hindu-Arabic numerals notation
- and the numerous contributions to mathematics from the Islamic world
Modern Era
In Modern times, after the period of about 1400 - 1650 and with the "import" of Number theory from the middle East, number theory advanced even further with the likes of Fermat, Euler, Lagrange, Gauss, Riemann and many more mathematicians and famous scientists.
Why Number Theory
Initially, number theory was considered a branch of mathematics with no practical uses nor relevance in the real world. Real-world applications of number theory began in the middle of the 20th century, with the arrival of computers and the dawn of the digital age.
Computers allowed number theorists to advance significantly in topics such as:
- factoring large numbers
- determining primes
- checking the validity of conjectures (unproven mathematical theorems)
Series Outline
In this series we will cover at least the following topics:
- Divisibility
- Prime numbers
- Modular Arithmetic
- Diophantine Equations
Of course, most of these will require multiple parts, so that we can get into full-on examples to make the problems and their solutions as clear as possible.
RESOURCES:
References
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Final words | Next up
And this is actually it for today's post!
Next time we will start getting into Divisibility.
See ya!

Keep on drifting!
Posted with STEMGeeks
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Well done our maths guru🙌🏿.
I hope you will make a collection of links to these posts later.
!discovery 43
This post was shared and voted inside the discord by the curators team of discovery-it
Join our community! hive-193212
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more