Mathematics - Number Theory - GCD and LCM

Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the "Number Theory" series, in order to get into GCD and LCM. The Greatest Common Divisor and Least Common Multiple are two very important numbers as they relate two (or more) integers. We already covered how the GCD can be calculated via Factorization and the Euclidean Algorithm in the 3rd part of the series. Today, we will cover the relationship between the GCD and LCM.
So, without further ado, let's dive straight into it!
Greatest Common Divisor (GCD)
The GCD or GCF (for greatest common factor) of two (or more) integers, is the largest positive integer which perfectly divides both (or all) of them.
Euclidean Algorithm Method
The Euclidean algorithm is maybe the most efficient way of calculating the GCD of two numbers. Basically, a division algorithm is combined with the property that the GCD has of being able to divide the difference of the two numbers.
For example, the GCD of 156 and 34 can be calculated as follows:
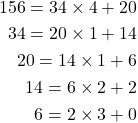
And so GCD(156, 34) = 2.
For more details on this method please check out the 3rd part of the series.
Prime Factorization Method
In the 3rd part we also covered a more time-consuming method involving the factorization of the numbers. Any compositve (non-prime) number can be represented as a product of primes and their combinations.
Having two numbers in this representation the GCD is then simply equal to product of the common prime factors.
For example, 156 is factorized as 22 × 3 × 13 and 34 as 2 × 17. So, as the only common prime factor is 2, 2 is also the GCD of 156 and 34.
Least Common Multiple (LCM)
The LCM, which is known as the least or lowest common multiple of two (or more) integers, is the smallest positive integer which can be divided by both (or all) of the integers.
Brute Force Method
The most basic way of finding the LCM is via a "brute force" method. Basically, all multiples of the integers are listed and in the worst case scenario the LCM will simply be the product of the two.
For example, the LCM of 16 and 30 can be checked as follows:
16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240
30: 30, 60, 90, 120, 150, 180, 210, 240
Thus, LCM(16, 30) = 240.
In the worst case scenario we would have to check up to 480 as 16 × 30 = 480.
Prime Factorization Method
Based on the factorization of two compositive numbers, the LCM is simply the product of the highest power of each of the prime numbers / factors.
For example, 16 is represented as 24 and 30 as 2 × 3 × 5.
Thus, the LCM of 16 and 30 is equal to 24 × 3 × 5 = 240.
Of course, this is also quite time-consuming...
GCD Method
Lastly, the LCM can also be calculated easily when knowing the GCD.
The following relationship holds for any two integers a and b:
LCM (a, b) = a × b ÷ GCD (a, b)
For example, the GCD of 16 and 30 is 2, which can easily be seen from the prime factorization. Multiplying the two numbers yields 480. And thus the LCM is simply 480 ÷ 2 = 240, which is the same exact result that we got via the other methods.
Exercise
Calculate the GCD and LCM of 384 and 120 by applying the Prime Factorization Method.
Hint: The LCM is below 2000. Please don't check up to 46080.
RESOURCES:
References
- https://brilliant.org/wiki/number-theory
- https://www.calculator.net/gcf-calculator.html
- https://www.calculator.net/lcm-calculator.html
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Number Theory, Why Number Theory, Series Outline
- Divisibility → Divisibility, Divisibility Rules
- Factorization and Euclidean Algorithm → Factorization, Euclidean Algorithm and GCD, Division Algorithm using Calculator
- Prime Numbers → Prime, Composite and Co-Prime Numbers, Prime Test (Sieve of Eratosthenes)
- Divisibility Examples → Divisibility Properties, Examples (Proof through Mathematical Induction, Properties, Solving Subproblems)
Final words | Next up
And this is actually it for today's post!
Next time we will get into Diophantine Equations.
See ya!

Keep on drifting!
Posted with STEMGeeks
nice class about number theories!

!1UP
You have received a 1UP from @gwajnberg!
@stem-curator
And they will bring !PIZZA 🍕.
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.