Mathematics - Discrete Mathematics - Sequences and Recurrence Relations
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Sequences and Recurrence Relations.
So, without further ado, let's get straight into it!
Sequences
Sequences are ordered lists of numbers. So, they are different from usual sets, where the order mostly doesn't matter. The sequence of all natural numbers is thus different from the set of all natural numbers (N).
Terms
A commonly used representation of the terms is:
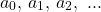
The entire sequence is usually represented by an . Of course, the letter a can be easily replaced with any other letter.
Sequences usually starts from term a0. The subscript is the index of the number in the sequence. So, a0 is the 0th term of the sequence.
Note: Having the 0th term be the first one in the sequence may be a little bit confusing (maybe not for computer scientists). If it's too confusing, using a1 as the first one is also feasible, but it should be mentioned in the sequence definition, in some way:
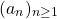
Definition
Sequences are commonly specified using functions. These are either closed formulas or recursive definitions.
A closed formula defines the nth term of the sequence only in terms of n.
For example:
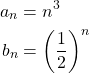
So, the term at index n = 3 is simply:
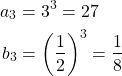
In recursive definitions (or relations) previous terms of the sequence are considered as well. Initial values need to be provided for the first terms of such sequences.
A widely-known recursive sequence is the Fibonacci sequence:
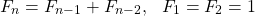
where each term is the sum of the two previous terms:
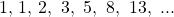
Arithmetic Sequences
If the terms differ only by a constant then the sequence is said to be arithmetic. Such sequences can be represented with either definition:
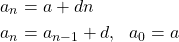
In these d is the difference between the terms and a the initial term of the sequence.
Geometric Sequences
If the ratio between successive terms is constant then the sequence is called geometric.
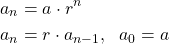
where r is the common ratio and a is the initial term.
Solving Recurrence Relations
Usually, sequences are easier to define in a recursive way. But, there's a way to convert them into closed formulas. This is basically a form of "solving" them. Some can be solved through "iteration" and "telescoping" while others require more complicated methods.
First of all, recurrence relations are basically difference equations with an order equal to the difference between the highest and lowest indices of the terms. These relations are solved by finding the roots of characteristic polynomials.
Solving the polynomial can easily become quite complicated...
For example, a recurrence relation of the form:
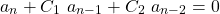
can be solved through the characteristic polynomial:
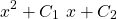
The roots of the equation:
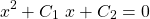
result in the solution of the recurrence relation, which is:
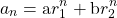
The constants a and b are determined from the initial conditions.
Recurrence relations of this form are linear homogeneous recurrence relations with constant coefficients.
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
Final words | Next up
And this is actually it for today's post!
Next time we will continue on with an Introduction to Probability Theory...
See ya!

Keep on drifting!
Posted with STEMGeeks