Mathematics - Discrete Mathematics - Relation Closures
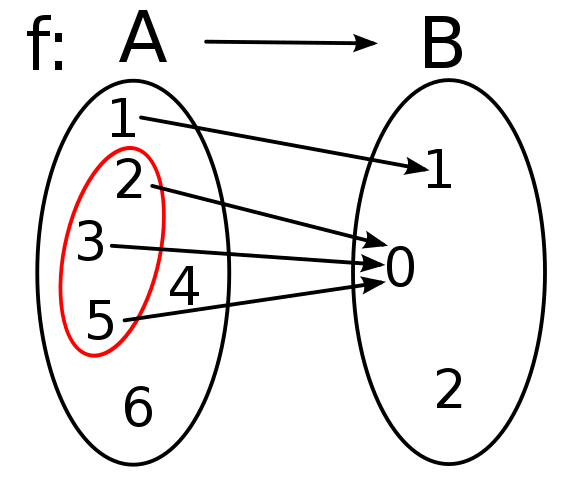
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Relation Closures.
So, without further ado, let's get straight into it!
Relation Closures
Consider a set A and the wide range of relations on A. In the previous part it was shown that these relations can satisfy various properties, such as being reflexive, symmetric or transitive. If P is such a property than a relation with property P is a P-relation.
P-Closure
A P-closure of any arbitrary relation R on A, indicated by P(R), is a P-relation, which is related to relation R as follows:
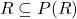
In other words, a P-closure is simply the process of adding the least amount of ordered pairs to R, such that R satisfies a given property P.
Reflexive Closure
The reflexive closure is easy to obtain.
For a given set A, Δ is the diagonal or equality relation on A, defined as:
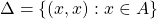
Δ is basically the smallest possible relation which satisfies the reflexive property on A.
Thus, for any given relation R on set A, obtaining the reflexive closure is simply a union operation of R with Δ:
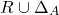
Symmetric Closure
The symmetric closure is also easy to obtain.
For a relation R on set A, R-1 is the inverse of R, such that:
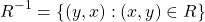
Obtaining the symmetric closure is thus simply a union operation of R with R-1:
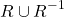
Transitive Closure
Obtaining a transitive closure is more complicated.
The transitive closure or connectivity relation or star closure of a relation R on set A with n-elements is obtained from the following equation:
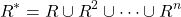
The exponentials of R indicate compositions of relations:
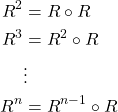
For two given sets R and S, the composition is defined as follows:
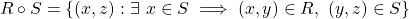
This is easier to calculate using a matrix multiplication technique, which will be explained in the example below...
Full-On Example
Consider the following set and relation:
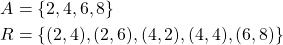
Let's calculate the three closures!
Reflexive Closure
The equality relation is:
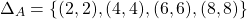
And so, the reflexive closure is:

Symmetric Closure
The inverse relation is:
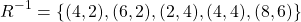
And thus, the symmetric closure is:

Transitive Closure
The relation can be re-written as a matrix:

where the rows are the first members and columns the second members. A '0' specifies the absence of the pair, whilst a '1' the presence of the pair.
The transitive (star) closure is the union of R, R2, R3 and R4.
Obtaining the corresponding MR2 matrix is as simple as multiplying the MR matrix by itself:
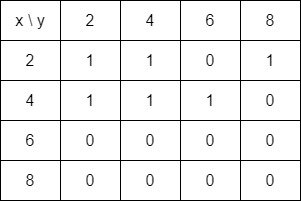
Only the absence or presence matters and so the result is kept in 0-1 format.
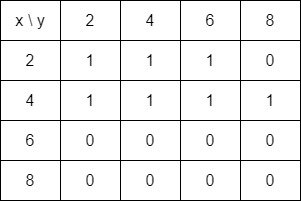
Obtaining MR3 is a multiplication of MR2 by MR, resulting in:
And lastly, MR4 = MR3 x MR, yielding:
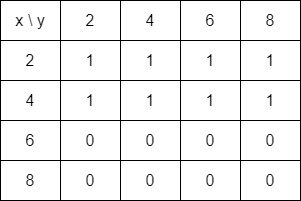
The transitive closure in matrix form, MR*, is the union of all these matrices and thus equal to:
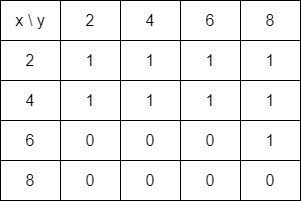
which can be represented in "set form" as follows:
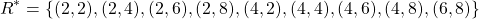
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
- https://people.cs.rutgers.edu/~elgammal/classes/cs205/chapt74.pdf
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
Final words | Next up
And this is actually it for today's post!
Next time we will continue on with more on Equivalence Relations and maybe even on Partial Order Relations, and the corresponding Partially Ordered Sets (POSET)...
See ya!

Keep on drifting!
Posted with STEMGeeks