Mathematics - Discrete Mathematics - Proof Strategies (part 1)

[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Proof Strategies. There will be two parts...
So, without further ado, let's get straight into it!
Proofs
The whole theoretical stuff around mathematical statements or propositions was interesting and all, but where does it come into use? Well, using propositional logic and the various rules and laws, it's possible to prove logic statements. This can be something simple like:
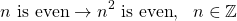
or get complicated quite easily as well...
Let's get into some of the strategies for proving mathematical statements.
Direct Proof
A direct proof is the simplest form of proof. These are particularly useful when proving implications (p → q). The conclusion is proven by combining mathematical axioms, definitions and theorems, which are known to be true.
The procedure is as follows:
- Assume p
- Explain...
- Deduce q
Examples
The statement from before can be proving directly...
If n is an arbitrary integer that is even then n = 2k for some integer k. For the square of n now:
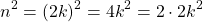
which is also even for any k.
Similarly, using direct proof it's also possible to prove that the sum of two even integers is even, as shown below:
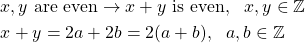
Proof by Contrapositive
Let's recall something from the previous parts: An implication p → q is logically equivalent to its contrapositive ¬q → ¬p. As such, when proving an implication directly seems too difficult, it's possible to prove by proving its contrapositive. In other words, assuming the that the conclusion is false (¬q) and deducing that the assumption is false (¬p).
Example
Let's proof:

This statement can't be proven directly, and so the contrapositive will be proven instead. The proof of the contrapositive looks like this:
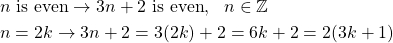
and so the contrapositive has been proven, which means that the original implication is also true.
Proof by Contradiction
There are statements which can't be easily expressed as implications. In such cases what can be useful is proving through contradiction:

In other words, if p ∧ ¬q is true, then through double negation the original implication p → q is true as well.
Example
A common example is proving that √2 is irrational.
Starting from the assumption that √2 is rational:
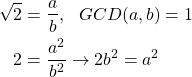
which means that a2, and as a result a, is divisible by 2, and so a = 2n.
But, then:
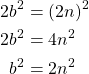
which makes b also divisible by 2.
Thus, the GCD(a, b) ≥ 2 and not 1, which makes the assumption false, meaning that √2 is irrational and not rational.
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
- https://ece.iisc.ac.in/~parimal/2015/proofs/lecture-02.pdf
- https://www.cs.amherst.edu/~djvelleman/pd/help/Strategies.html
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
Final words | Next up
And this is actually it for today's post!
Next time we will continue with part 2...
See ya!

Keep on drifting!
Posted with STEMGeeks
What a very nice and informative post. Thanks for sharing with us