Mathematics - Discrete Mathematics - Conditional Probability
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Conditional Probability.
I highly suggest checking the post on Probability before this one!
So, without further ado, let's get straight into it!
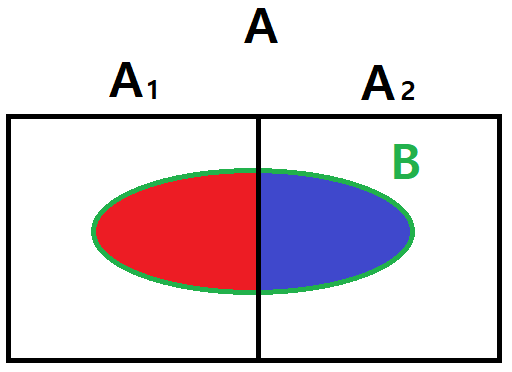
Conditional Probability
For dependent events, where the occurrence of one affects the outcome of another, a new kind of probability is defined known as conditional probability. The probability of an event A from occurring when an event B has already occurred is denoted as P(A | B), and given by:
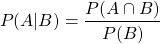
Solving for the intersection, results in:
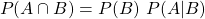
In a similar manner, the probability of event B from occurring when A has occurred is:
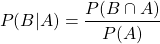
If the events A and B are independent then:
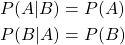
Law of Total Probability
Based on conditional probability, it's possible to calculate the total probability of an event B for any number of disjoint events Ai. The resulting equation is known as the law of total probability:
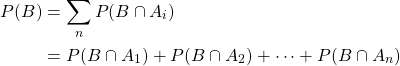
Each intersection can also be replaced with the corresponding conditional probability equation yielding:
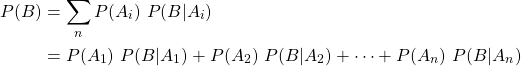
Bayes' Theorem
Let's not forget to mention Bayes' Theorem, which is basically an equation that relates P(A | B) and P(B | A).
It's easy to derive such an equation from the definition of conditional probability:

Note: Of course commutativity applies for the intersection of A and B.
So, knowing P(A), P(B) and either of the two it's possible to calculate the other using this equation.
Full-On Example
Consider a bowl is filled with 3 black and 5 white marbles. What's the probability of picking:
- two consecutive black marbles
- black marble followed by white marble
- three consecutive black marbles
- a black marble in the second pick
The overall number of marbles is 8, and so the probabilities of picking a black and white marble respectively are initially:
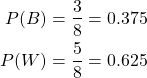
Two consecutive black marbles
After picking a black marble, 7 marbles will be remaining, with only 2 being black. The probability of picking a second black marble, after a black one has already been picked, is thus:
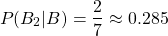
And so, the total probability for picking two consecutive black marbles is:

Black marble followed by white marble
After picking a black marble, 5 out of the 7 remaining ones will be white. So, the probability of picking a white one after a black marble is:

As such, the total probability for picking a black marble followed by a white marble is:
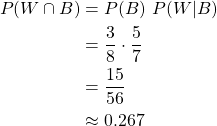
Bonus: Of course, the order doesn't matter in this problem, as picking a white one and then a black one has the same probability (it's simply the intersection of B and W in either order). As such, after picking a white one 3 black marbles will remain, giving the same total probability of:
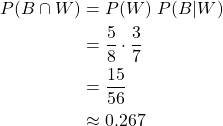
Three consecutive black marbles
After two black marbles have already been picked, picking a third marble has a probability of:
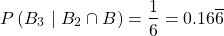
as 6 marbles will remain with only 1 being black.
As such, the total probability is:

In other words, the probability is basically the product:
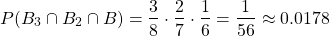
as each pick depends on the previous pick.
Black marble in second pick
This last case is a great example of the law of total probability!
Because it's uncertain what came first, the probability will be a sum of two cases:
- black marble was picked first
- white marble was picked first
So, picking a black marble in the second pick has a probability of:
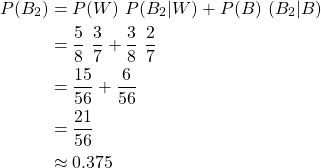
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
- https://www.investopedia.com/terms/b/bayes-theorem.asp
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
- Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
- Probability → Probability Theory, Probability, Theorems, Example
Final words | Next up
And this is actually it for today's post!
Next time we will get into an overview of Graph Theory...
See ya!

Keep on drifting!
Posted with STEMGeeks
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.