Mathematics - Discrete Mathematics - Common Graph Problems
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Common Graph Problems.
So, without further ado, let's get straight into it!
Graph Theory Applications
The applications of Graph Theory are basically countless. Many problems (and subproblems) can be solved using the various graph types and representations. With this article a small overview on some of these problems will be made. There are many known algorithms that can be used in order to solve them, which will be mentioned without further explanation...
Shortest Path Problem
First and foremost, the most common graph problem is finding the shortest path from one node to another. This of course only makes sense in the context of a weighted graph. The shortest path is the path with the least possible sum of weights.
For example, in the graph below travelling from vertex A to vertex F "costs" 20. On the other, hand if the upper path was taken instead (A → B → D → F) the cost would be 25.
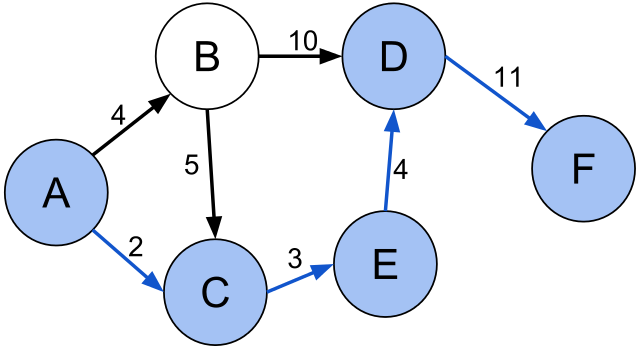
[Image 2]
The two most commonly used algorithms for finding the shortest path from a single source vertex are Dijkstra's algorithm and Bellman-Ford's algorithm. Additionally there are also algorithms like Floyd-Warshall's and Johnson's which solve for shortest paths between all possible pairs.
Graph Connectivity
In many cases, it may be important to know if a path exists from a given node to another. In that case the graph is traversed using either Breadth First Search (BFS) or Depth First Search (DFS) in order to check if the nodes are connected.
The required result in many problems has to be a connected graph, and so a "connectivity check" may have to be applied between all possible node pairs.
Travelling Salesman Problem (TSP)
An easy to understand problem with lots of real-world applications is TSP. A salesman wants to visit a list of cities. Between each pair of cities there is a travelling cost. Each city is visited once and the first and last city are one and the same. In other words, the problem is about finding the Hamiltonian cycle with the least travelling cost.
The problem may seem simple at first, but finding the optimal solution is computationally complicated. There are many algorithms for solving it such as branch and bound and Held - Karp, which commonly apply estimations and heuristics in order to speed-up the process of finding at least a valid solution.
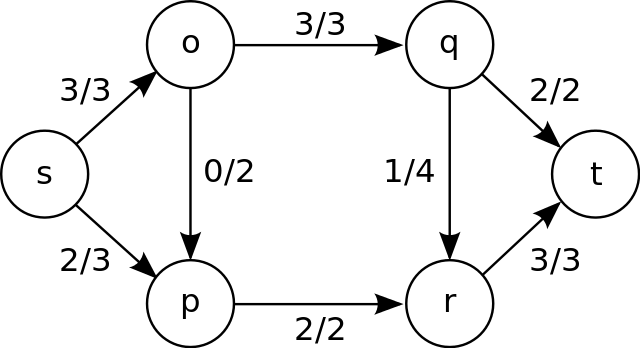
Minimum Spanning Tree
Another common problem is finding the minimum-cost spanning tree in a given graph. A spanning tree connects all vertices from the original graph, but with the least possible overall cost. The problem can be solved using Kruskal's and Prim's algorithms.

[Image 3]
Maximum Network Flow
Let's not forget to mention the problem of maximizing network flow. The weights in the graph may be used to visualize the capacity of each edge. In that sense, maximizing the "grid" and predicting bottlenecks can be very useful. Commonly used algorithms are Fork-Fulkerson's and Edmond-Karp's.
[Image 4]
Graph Coloring
Lastly, there is also graph coloring. Graphs are basically assigned labels, so that two adjacent vertices don't share one. The chromatic number of a graph is the minimum number of such colorings that has to be assigned. It's more commonly applied on vertices and not edges.
For example, a map can be seen as a graph where different colors are applied to neighboring countries. In that case, there also is no need to apply more than four colors, as a theorem known as the four-color theorem applies in the case of such planar graphs.
[Image 5]
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
- https://commons.wikimedia.org/wiki/File:UbMjAyAmQrSwtP0gdeKe_matchingshortcut.png
- https://commons.wikimedia.org/wiki/File:Shortest_path_with_direct_weights.svg
- https://commons.wikimedia.org/wiki/File:Minimum_spanning_tree.svg
- https://commons.wikimedia.org/wiki/File:Max_flow.svg
- https://commons.wikimedia.org/wiki/File:Graph_b_coloring_example.svg
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
- Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
- Probability → Probability Theory, Probability, Theorems, Example
- Conditional Probability → Conditional Probability, Law of Total Probability, Bayes' Theorem, Full-On Example
- Graphs → Graph Theory, Graphs (Vertices, Types, Handshake Lemma)
- Graphs 2 → Graph Representation (Adjacency Matrix and Lists), Graph Types and Properties (Isomorphic, Subgraphs, Bipartite, Regular, Planar)
- Paths and Circuits → Paths, Circuits, Euler, Hamilton
- Trees → Trees (Rooted, General and Binary), Tree Traversal, Spanning Trees
Final words | Next up
And this is actually it for today's post!
Next time we will talk about Binary Operations...
See ya!

Keep on drifting!
Posted with STEMGeeks
Tienes toda una colección de interesantes explicaciones aquí. Las matemáticas son un mundo fascinante. Quizá muchos más se interesarían en ellas si se esmeraran en ver más a fondo sus aplicaciones en su vida diaria, más allá de los cálculos básicos en el supermercado.
!1UP
You have received a 1UP from @latino.romano!
@stem-curatorAnd they will bring !PIZZA 🍕
Learn more about our delegation service to earn daily rewards. Join the family on Discord.