Mathematics - Discrete Mathematics - Combinatorial Principles

about 2 years ago

Introduction

Hey it's a me again @drifter1!

Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Combinatorial Principles.

So, without further ado, let's get straight into it!

Combinatorics

Combinatorics is a mathematics branch which studies counting and arranging of quantities. Together with Discrete Probability it is extremely useful in Computer Science. Counting techniques from Combinatorics are used in order to estimate the steps of an algorithm, as well as the possible outcomes through probability.

Basic Counting Principles

Let's start out with the simplest counting problems...

Additive Principle

Consider two events A and B. A can occur in m ways, whilst B in n ways. Additionally, the events are unrelated or disjoint.

If the events cannot occur simultaneously, how many ways does A or B occur?

The additive principle states that the event A or B occurs in m + n ways.

In general, for k disjoint events, the "sum" event occurs in:

In the context of sets, the additive principle can be written as:

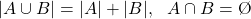
The principle easily extends to any number of disjoint sets...

Multiplicative Principle

Let's again consider the same disjoint events A and B. Both events occur independently. Choosing one of the m ways of A allows for exactly n ways on B afterwards.

So, if one of each is chosen, how many ways does A and B occur?

The multiplicative principle states that the event A and B occurs in m ⋅ n ways.

Note: The solution may be a product (⋅), but it's important to use the and word for the event combination.

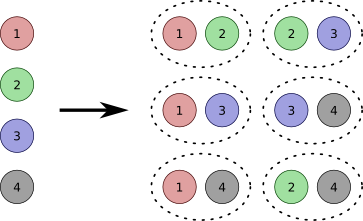
In the context of sets, the multiplicative principle is basically the cartesian product of A and B. The number of possible ways is the cardinality of the set of all possible ordered pairs (a, b), where a ∈ A and b ∈ B:

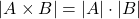
It may be easier to think of A x B as the union of m disjoint sets. Each set has n ways to occur, and so by applying the additive principle:

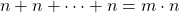
Example

Suppose a school class has 7 boys and 11 girls. How many different choices are there for choosing only one student? Additionally, if two are chosen, but one must be a boy and one a girl, how many combinations are there?

Applying the additive principle, the number of total choices is 7 + 11 = 18.

Applying the multiplicative principle, the number of combinations between boys and girls is 7 ⋅ 11 = 77.

Inclusion-Exclusion Principle

What if the events or sets are not disjoint? Well, then the same combination will be counted more than once. This problem is known as double counting. In order to solve this problem the inclusion-exclusion principle (or PIE) is applied.

2 Sets

The simplest case are two sets. Having two finite sets A and B, the cardinality of the union is simply:

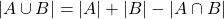
in other words |A| and |B| are included and |A ∩ B| is excluded, because it results in double counting.

3 Sets

In the case of three finite sets A, B and C, the result is a little more complicated:

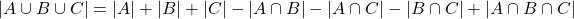
First, all elements are included. Then, the double counting between two sets is excluded. But, while excluding those, some elements where completely removed / uncounted. Thus, those elements are added back at the end, by including the intersection of all sets.

Such problems are easier to comprehend using Venn diagrams.

Example

An examination in three subjects A, B and C was taken by total of 35 students. The following table shows how many students passed each subject:

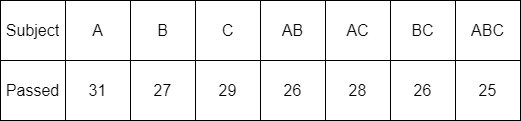
Try answering the following questions:

How many passed at least one subject?
How many failed at all subjects?
How many passed only subject A?
How many passed A and C but failed B?

The first question is simply the cardinality of the union of the three sets. The result is thus:

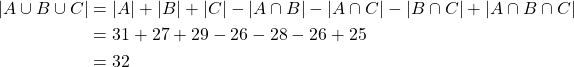
The second question is also simple. Because 32 passed at least one subject, 35 - 32 = 3 failed at all subjects.

The last two are more tricky to express! Let's thus use a Venn Diagram in order to visualize the problem.

First of all, 25 passed all three subjects and so the intersection of all three circles can be filled with a "25". Additionally, we know that 3 failed at all subjects, and so a "3" can be put outside:

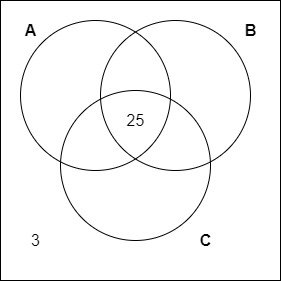
Now only 7 more students need to be "placed" on the Venn Diagram.

A ∩ B contains 26 elements from which 25 have already been counted, and so a "1" will be placed on the diagram. In a similar manner, only 3 of A ∩ C and 1 of B ∩ C haven't been counted yet, and so a "3" and "1" will be placed for these cases. The result is:

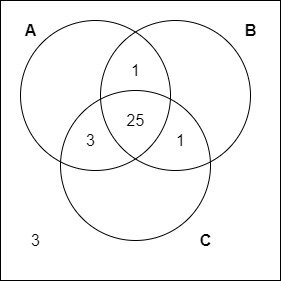
Now only 2 more student need to be placed!

Counting the elements of A, they are 25 + 3 + 1 = 29, and so 2 are missing, which is what comes in the last circle of A. For the other two sets, B has already 27 and C has already 29, and so "0"s fill be placed instead. The final result is:

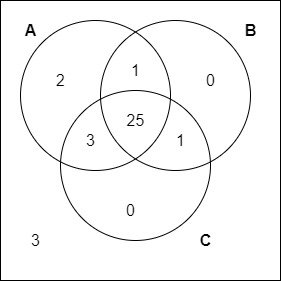
So, how many passed only A? Well, the answer is now clear as day, it is 2.

And, how many passed A and C but failed B? Well, it is 2 + 3 + 0 = 5, as the intersection of A and B isn't considered.

RESOURCES:

References

Images

https://commons.wikimedia.org/wiki/File:Combination.png

Mathematical equations used in this article, have been generated using quicklatex.

Block diagrams and other visualizations were made using draw.io.

Previous articles of the series

Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
Set Operations → Venn Diagrams, Set Operations, Properties and Laws
Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices